广东省深圳中学2023-2024学年九年级下学期开学试题数学试题(无答案)
文档属性
| 名称 | 广东省深圳中学2023-2024学年九年级下学期开学试题数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 599.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 20:48:58 | ||
图片预览

文档简介
2023-2024学年第二学期寒假学习评估
九年级数学试题
说明:
1.答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上.
2.考生必须在答题卷上按规定作答:凡在试卷、草稿纸上作答的,其答案一律无效.
3.全卷共6页,考试时间90分钟,满分100分.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.的倒数是( )
A.2024 B. C. D.
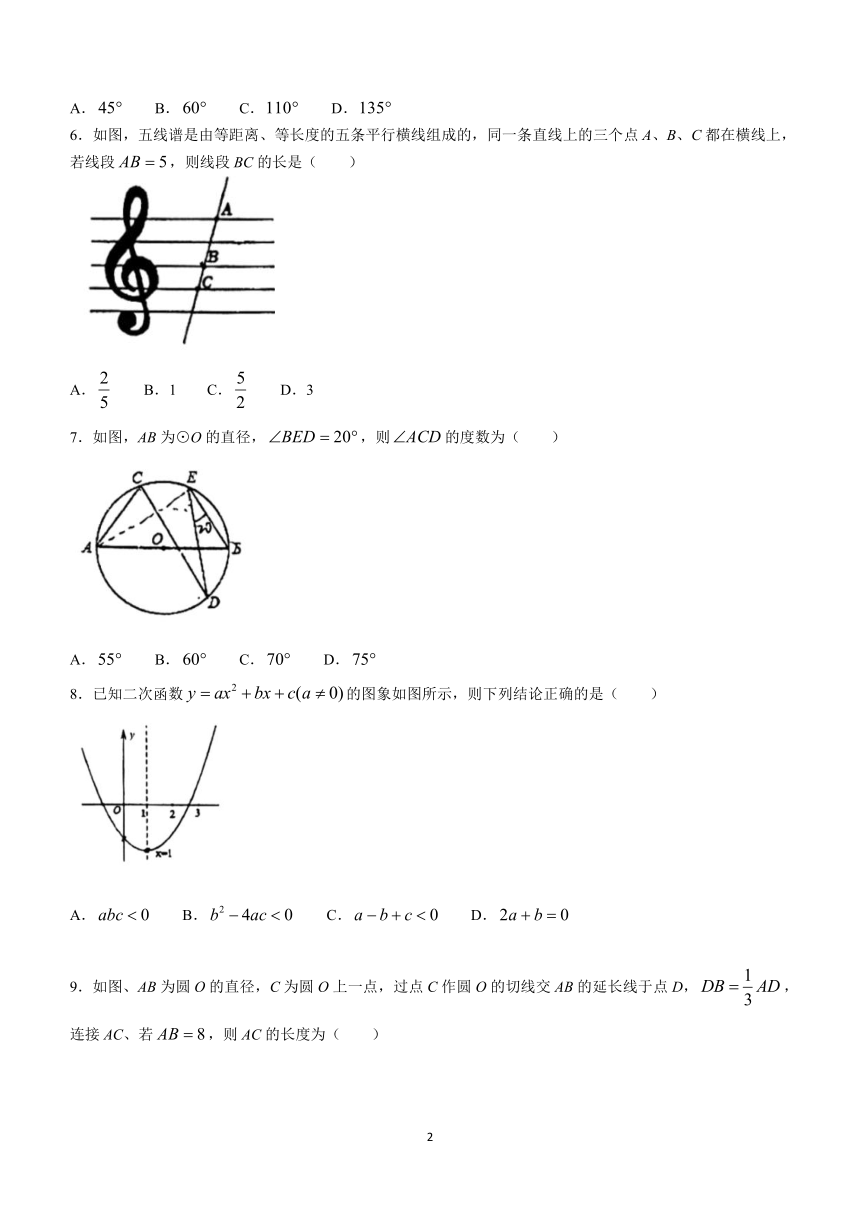
2.我国古代数学家刘徽利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B. C. D.
3.在平行四边形ABCD中,对角线AC与BD相交于点O.下列说法不能使平行四边形ABCD为菱形的是( )
A. B. C. D.
4.下列函数中,y的值随x的值增大而减小的是( )
A. B. C. D.
5.如图是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,则正八边形的一个外角( )
A. B. C. D.
6.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A、B、C都在横线上,若线段,则线段BC的长是( )
A. B.1 C. D.3
7.如图,AB为⊙O的直径,,则的度数为( )
A. B. C. D.
8.已知二次函数的图象如图所示,则下列结论正确的是( )
A. B. C. D.
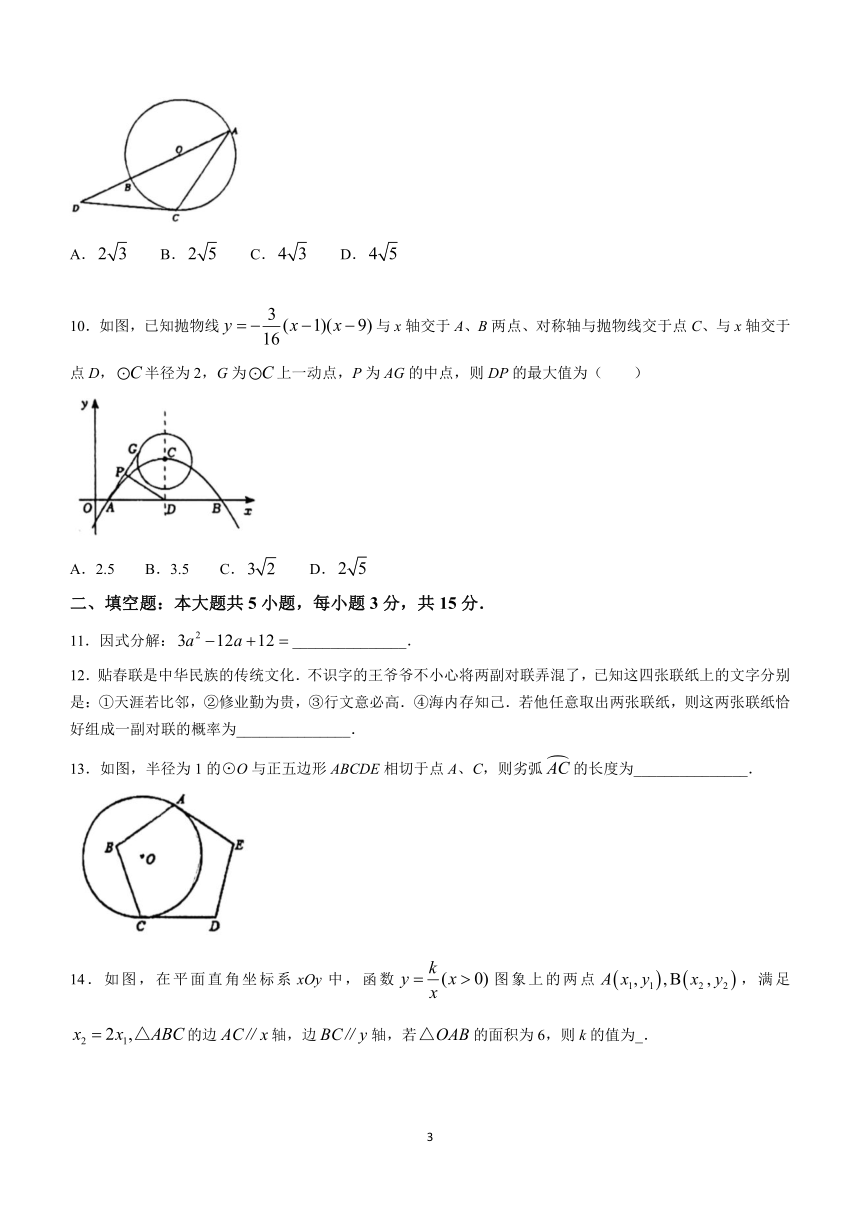
9.如图、AB为圆O的直径,C为圆O上一点,过点C作圆O的切线交AB的延长线于点D,,连接AC、若,则AC的长度为( )
A. B. C. D.
10.如图,已知抛物线与x轴交于A、B两点、对称轴与抛物线交于点C、与x轴交于点D,半径为2,G为上一动点,P为AG的中点,则DP的最大值为( )
A.2.5 B.3.5 C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.因式分解:_______________.
12.贴春联是中华民族的传统文化.不识字的王爷爷不小心将两副对联弄混了,已知这四张联纸上的文字分别是:①天涯若比邻,②修业勤为贵,③行文意必高.④海内存知己.若他任意取出两张联纸,则这两张联纸恰好组成一副对联的概率为_______________.
13.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧的长度为_______________.
14.如图,在平面直角坐标系xOy中,函数图象上的两点,满足的边轴,边轴,若的面积为6,则k的值为_.
15.如图,在中,,点D,E分别在边AB,AC上,且,,连接BE,CD,相交于点O,则面积最大值为_______________.
三、解答题(本题共7小题,共55分)
16.(本题5分)计算:
17.(本题8分)二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录.小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“A.惊蛰”“B.夏至”C.“白露”D.“霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.
(1)小明从四张卡片中随机抽取一张卡片、抽到“A.惊蛰”的概率是_______________.
(2)小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“B.夏至”的概率.
18.(本题8分)大鹏所城销售一种文创书签,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元.设该书签的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.(不需要写出x的取值范围)
(2)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
19.(本题8分)综合与实践活动中,要利用测角仪测量塔的高度,如图,塔AB前有一座高为DE的观景台,已知,点E,C,A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为,在观景台D处测得塔顶部B的仰角为.
(1)_______________.
(2)设塔AB的高度为h(单位:m);
①用含有h的式子表示线段EA的长,则_______________.(结果保留根号);
②求塔AB的高度(取0.5、取1.7,结果取整数).
20.(本题8分)已知AB是圆O的直径.点C是圆O上一点.点P为圆O外一点,且.
(1)求证:PA为圆O的切线;
(2)如果,求AC的长.
21.(本题8分)随着自动化设备的普及.公园中引入了自动喷灌器系统.该喷灌器可垂直升降,从喷水口喷出的水柱均为形状相同的抛物线,图1是该喷灌器喷水时的截面示意图.
图1 图2
(1)喷水口A离地高度为,喷出的水柱在离喷水口水平距离为处达到最高,高度为,且水柱刚好落在公园围栏和地面的交界B处.以点O为坐标原点,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系(如图2).
①求出该抛物线的解析式;
②求喷灌器底端O到点B的距离;
(2)现准备在公园内沿围栏建花坛.花坛的截面示意图为矩形BCDE(如图3),其中高CD为,宽CB为.为达到给花坛喷灌的效果,需将喷水口A向上升高,使水柱落在花坛的上方DE边上,则h的取值范围为_______________.
图3
22.(本题10分)【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连结AE,DF,且.交于点G,若,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
(2)【初步运用】如图2,在中,,点D为AC的中点,连结BD,过点A作交于点E,交BC于点F,求的值.
(3)【灵活运用】如图3,在四边形ABCD中,,点E,F分别在边AB,AD上,且,垂足为G,则_______________.
图1 图2 图3
九年级数学试题
说明:
1.答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上.
2.考生必须在答题卷上按规定作答:凡在试卷、草稿纸上作答的,其答案一律无效.
3.全卷共6页,考试时间90分钟,满分100分.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.的倒数是( )
A.2024 B. C. D.
2.我国古代数学家刘徽利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是( )
A. B. C. D.
3.在平行四边形ABCD中,对角线AC与BD相交于点O.下列说法不能使平行四边形ABCD为菱形的是( )
A. B. C. D.
4.下列函数中,y的值随x的值增大而减小的是( )
A. B. C. D.
5.如图是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,则正八边形的一个外角( )
A. B. C. D.
6.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A、B、C都在横线上,若线段,则线段BC的长是( )
A. B.1 C. D.3
7.如图,AB为⊙O的直径,,则的度数为( )
A. B. C. D.
8.已知二次函数的图象如图所示,则下列结论正确的是( )
A. B. C. D.
9.如图、AB为圆O的直径,C为圆O上一点,过点C作圆O的切线交AB的延长线于点D,,连接AC、若,则AC的长度为( )
A. B. C. D.
10.如图,已知抛物线与x轴交于A、B两点、对称轴与抛物线交于点C、与x轴交于点D,半径为2,G为上一动点,P为AG的中点,则DP的最大值为( )
A.2.5 B.3.5 C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11.因式分解:_______________.
12.贴春联是中华民族的传统文化.不识字的王爷爷不小心将两副对联弄混了,已知这四张联纸上的文字分别是:①天涯若比邻,②修业勤为贵,③行文意必高.④海内存知己.若他任意取出两张联纸,则这两张联纸恰好组成一副对联的概率为_______________.
13.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧的长度为_______________.
14.如图,在平面直角坐标系xOy中,函数图象上的两点,满足的边轴,边轴,若的面积为6,则k的值为_.
15.如图,在中,,点D,E分别在边AB,AC上,且,,连接BE,CD,相交于点O,则面积最大值为_______________.
三、解答题(本题共7小题,共55分)
16.(本题5分)计算:
17.(本题8分)二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录.小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“A.惊蛰”“B.夏至”C.“白露”D.“霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.
(1)小明从四张卡片中随机抽取一张卡片、抽到“A.惊蛰”的概率是_______________.
(2)小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“B.夏至”的概率.
18.(本题8分)大鹏所城销售一种文创书签,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元.设该书签的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.(不需要写出x的取值范围)
(2)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
19.(本题8分)综合与实践活动中,要利用测角仪测量塔的高度,如图,塔AB前有一座高为DE的观景台,已知,点E,C,A在同一条水平直线上.某学习小组在观景台C处测得塔顶部B的仰角为,在观景台D处测得塔顶部B的仰角为.
(1)_______________.
(2)设塔AB的高度为h(单位:m);
①用含有h的式子表示线段EA的长,则_______________.(结果保留根号);
②求塔AB的高度(取0.5、取1.7,结果取整数).
20.(本题8分)已知AB是圆O的直径.点C是圆O上一点.点P为圆O外一点,且.
(1)求证:PA为圆O的切线;
(2)如果,求AC的长.
21.(本题8分)随着自动化设备的普及.公园中引入了自动喷灌器系统.该喷灌器可垂直升降,从喷水口喷出的水柱均为形状相同的抛物线,图1是该喷灌器喷水时的截面示意图.
图1 图2
(1)喷水口A离地高度为,喷出的水柱在离喷水口水平距离为处达到最高,高度为,且水柱刚好落在公园围栏和地面的交界B处.以点O为坐标原点,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系(如图2).
①求出该抛物线的解析式;
②求喷灌器底端O到点B的距离;
(2)现准备在公园内沿围栏建花坛.花坛的截面示意图为矩形BCDE(如图3),其中高CD为,宽CB为.为达到给花坛喷灌的效果,需将喷水口A向上升高,使水柱落在花坛的上方DE边上,则h的取值范围为_______________.
图3
22.(本题10分)【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连结AE,DF,且.交于点G,若,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
(2)【初步运用】如图2,在中,,点D为AC的中点,连结BD,过点A作交于点E,交BC于点F,求的值.
(3)【灵活运用】如图3,在四边形ABCD中,,点E,F分别在边AB,AD上,且,垂足为G,则_______________.
图1 图2 图3
同课章节目录
