六年级下册数学人教版5.1 抽屉原理课件(共21张PPT)
文档属性
| 名称 | 六年级下册数学人教版5.1 抽屉原理课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:23:16 | ||
图片预览




文档简介
(共21张PPT)
第五单元 抽屉原理
5.1 抽屉原理
一、复习回顾
激趣导入
看到这个课题,你们心里有什么好奇的地方呢?
自主学习
根据这个信息,你能提出哪些数学问题?
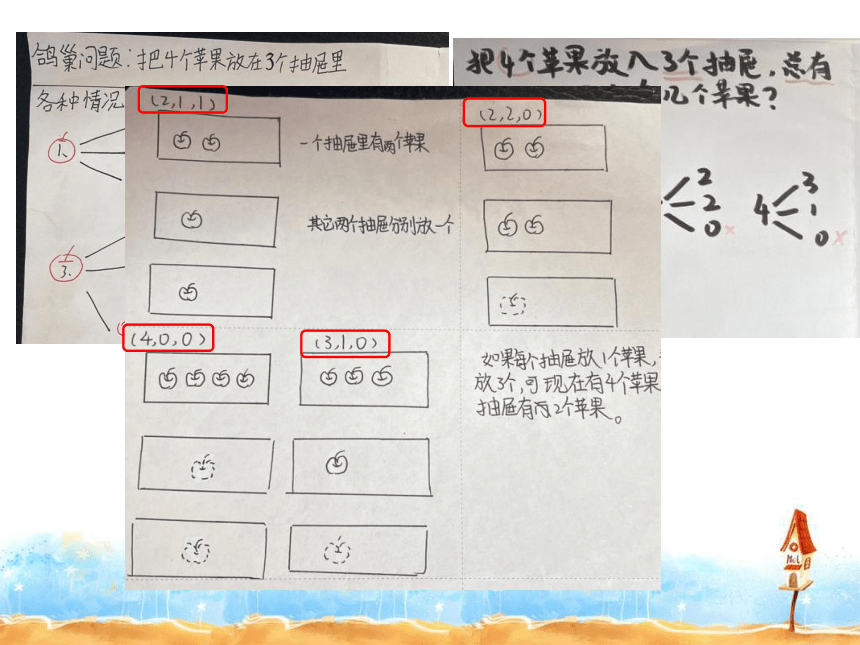
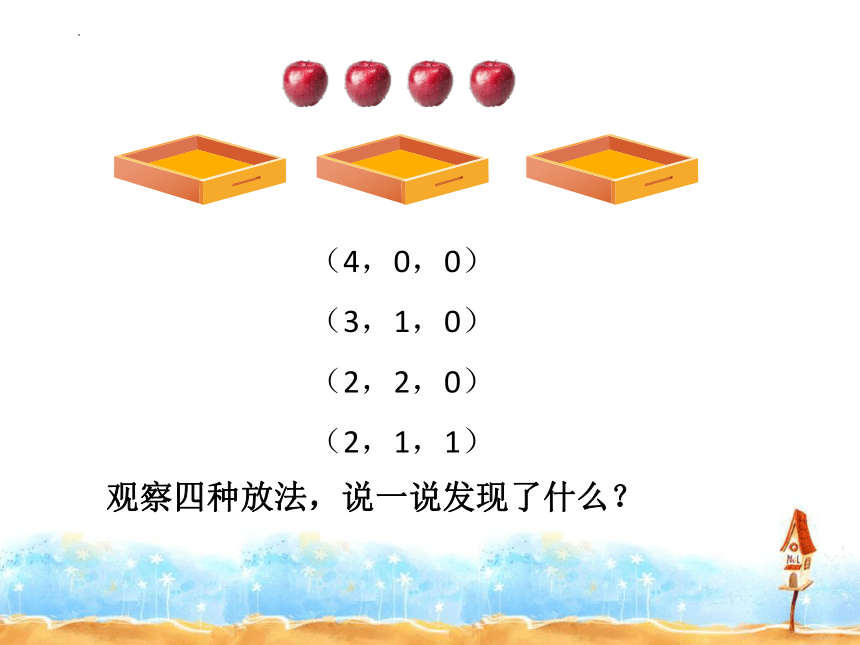
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
观察四种放法,说一说发现了什么?
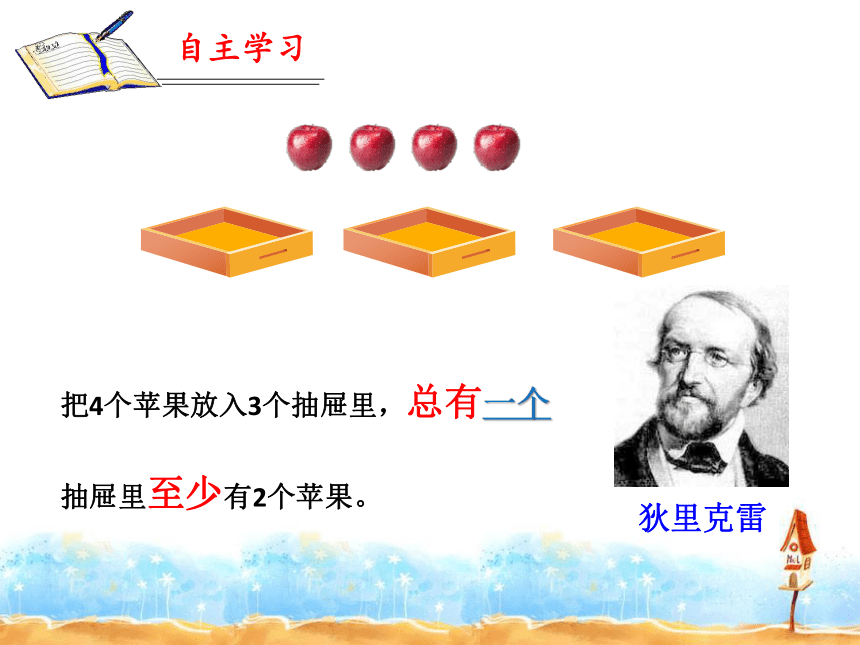
狄里克雷
自主学习
把4个苹果放入3个抽屉里,总有一个抽屉里至少有2个苹果。
把5个苹果放入4个抽屉里,总有一个抽屉里至少有2个苹果。
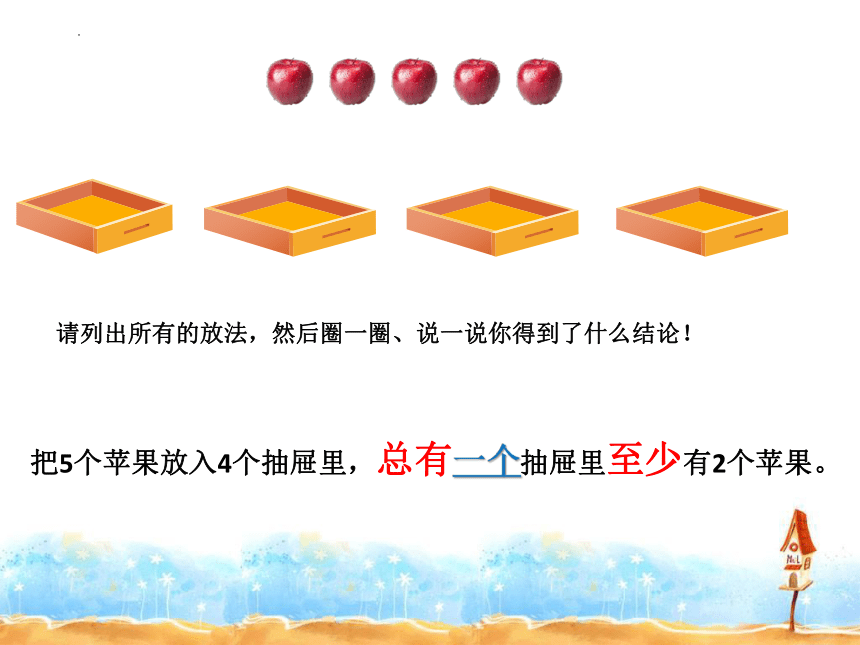
请列出所有的放法,然后圈一圈、说一说你得到了什么结论!
这明明“是2个”,凭什么说“至少有2个”?
把4个苹果放在3个抽屉里,总有一个抽屉里至少有2个苹果
把5个苹果放在4个抽屉里,
把6个苹果放在5个抽屉里,
把10个苹果放在9个抽屉里,
把100个苹果放在99个抽屉里,
·······
不管怎么放,总有一个抽屉里至少有2个苹果。
把(n+1)支笔放到 n 个笔筒中,
总有一个笔筒里至少有 2 支笔。
狄利克雷
“抽屉原理”也叫“鸽巢问题”
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
知
能
应
用
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
7只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
8只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
9只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
3
2
联
系
生
活
6÷4=1(只)·······2(只) 1+1=2(只)
7÷4=1(只)·······3(只) 1+1=2(只)
8÷4=2(只)
9÷4=2(只)·······1(只)
2+1=3(只)
苹果数÷抽屉数=商······余数 至少数= 商+1
将100个苹果放在10个抽屉里,还需要+1吗?
把4个苹果放在3个抽屉里,总有一个抽屉里至少有2个苹果。
4÷3=1······1 1+1=2
1.随意找13位同学,他们中至少有2个人的出生月份相同。
为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
一月
二月
三月
四月
五月
六月
七月
八月
九月
十月
十一月
十二月
答:假设12位同学分别出生在12个不同的月份,那么第13位同学无论出生在哪个月份,其中至少有2位同学出生月份相同。
2.随意找13位老师,他们中至少有2个人的生肖相同。为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
答:假设12位老师分别属于12生肖属相,那么第13位老师无论属于哪一种属相,其中至少有2位老师属相相同。
3.四人小组玩剪刀、石头、布的游戏,不管怎样出,总有一
种手势至少有两个人同时出。为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
答:假设前3位同学分别出了3种不同的手势,那么第4位同学无论出哪一种手势,其中至少有2位同学手势相同。
第五单元 抽屉原理
5.1 抽屉原理
一、复习回顾
激趣导入
看到这个课题,你们心里有什么好奇的地方呢?
自主学习
根据这个信息,你能提出哪些数学问题?
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
观察四种放法,说一说发现了什么?
狄里克雷
自主学习
把4个苹果放入3个抽屉里,总有一个抽屉里至少有2个苹果。
把5个苹果放入4个抽屉里,总有一个抽屉里至少有2个苹果。
请列出所有的放法,然后圈一圈、说一说你得到了什么结论!
这明明“是2个”,凭什么说“至少有2个”?
把4个苹果放在3个抽屉里,总有一个抽屉里至少有2个苹果
把5个苹果放在4个抽屉里,
把6个苹果放在5个抽屉里,
把10个苹果放在9个抽屉里,
把100个苹果放在99个抽屉里,
·······
不管怎么放,总有一个抽屉里至少有2个苹果。
把(n+1)支笔放到 n 个笔筒中,
总有一个笔筒里至少有 2 支笔。
狄利克雷
“抽屉原理”也叫“鸽巢问题”
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
知
能
应
用
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
6只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
7只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
8只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
2
9只鸽子飞进4个鸽笼,
总有一个鸽笼至少飞进( )只鸽子。
3
2
联
系
生
活
6÷4=1(只)·······2(只) 1+1=2(只)
7÷4=1(只)·······3(只) 1+1=2(只)
8÷4=2(只)
9÷4=2(只)·······1(只)
2+1=3(只)
苹果数÷抽屉数=商······余数 至少数= 商+1
将100个苹果放在10个抽屉里,还需要+1吗?
把4个苹果放在3个抽屉里,总有一个抽屉里至少有2个苹果。
4÷3=1······1 1+1=2
1.随意找13位同学,他们中至少有2个人的出生月份相同。
为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
一月
二月
三月
四月
五月
六月
七月
八月
九月
十月
十一月
十二月
答:假设12位同学分别出生在12个不同的月份,那么第13位同学无论出生在哪个月份,其中至少有2位同学出生月份相同。
2.随意找13位老师,他们中至少有2个人的生肖相同。为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
答:假设12位老师分别属于12生肖属相,那么第13位老师无论属于哪一种属相,其中至少有2位老师属相相同。
3.四人小组玩剪刀、石头、布的游戏,不管怎样出,总有一
种手势至少有两个人同时出。为什么?
http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
知能应用
答:假设前3位同学分别出了3种不同的手势,那么第4位同学无论出哪一种手势,其中至少有2位同学手势相同。
