人教版七年级下册数学 5.2平行线的判定同步练习(含解析)
文档属性
| 名称 | 人教版七年级下册数学 5.2平行线的判定同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:13:48 | ||
图片预览



文档简介
人教版七年级下册数学5.2 平行线的判定同步练习
一、单选题
1.在同一平面内,若,则b与c的关系为( )
A.平行或重合 B.平行或垂直 C.垂直 D.相交
2.如图,下面能判断的条件是( )
A. B. C. D.
3.下列条件能判定的是( )
A. B. C. D.
4.如图,下列条件中,能判断的是( )
A. B.
C. D.
5.如图,点 E 在 的延长线上,下列条件中能判断的是( )
A. B. C. D.
6.如图,下列条件中不能判断的是( )
A. B. C. D.
7.如图,在下列给出的条件中,能判定的是( )
A. B. C. D.
8.如图所示,以下5个条件:①;②;③;④;⑤.其中一定能判定的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.如图,点是延长线上一点,请添加一个你认为恰当的条件 ,使.
10.如图,,平分,则与的位置关系是 .
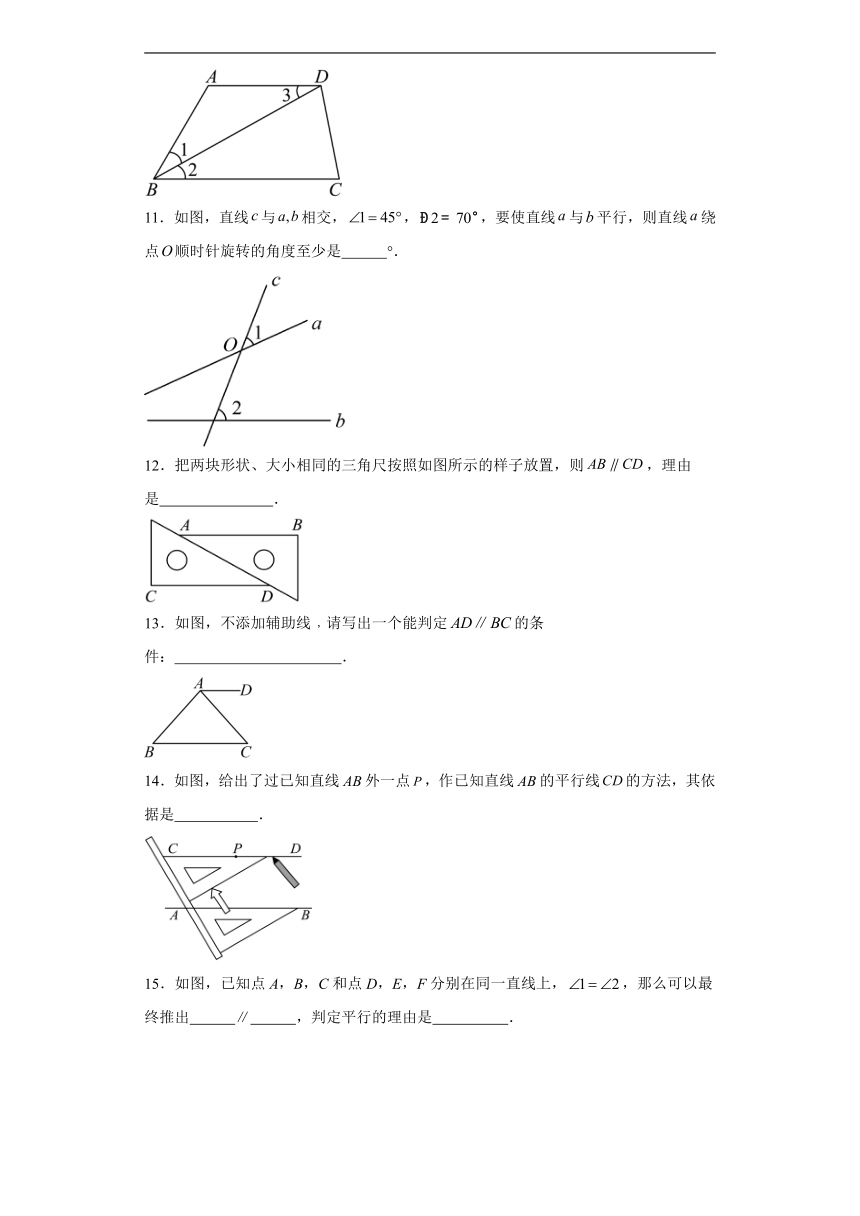
11.如图,直线与相交,,,要使直线与平行,则直线绕点顺时针旋转的角度至少是 °.
12.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
13.如图,不添加辅助线﹐请写出一个能判定的条件: .
14.如图,给出了过已知直线外一点,作已知直线的平行线的方法,其依据是 .
15.如图,已知点A,B,C和点D,E,F分别在同一直线上,,那么可以最终推出 ∥ ,判定平行的理由是 .
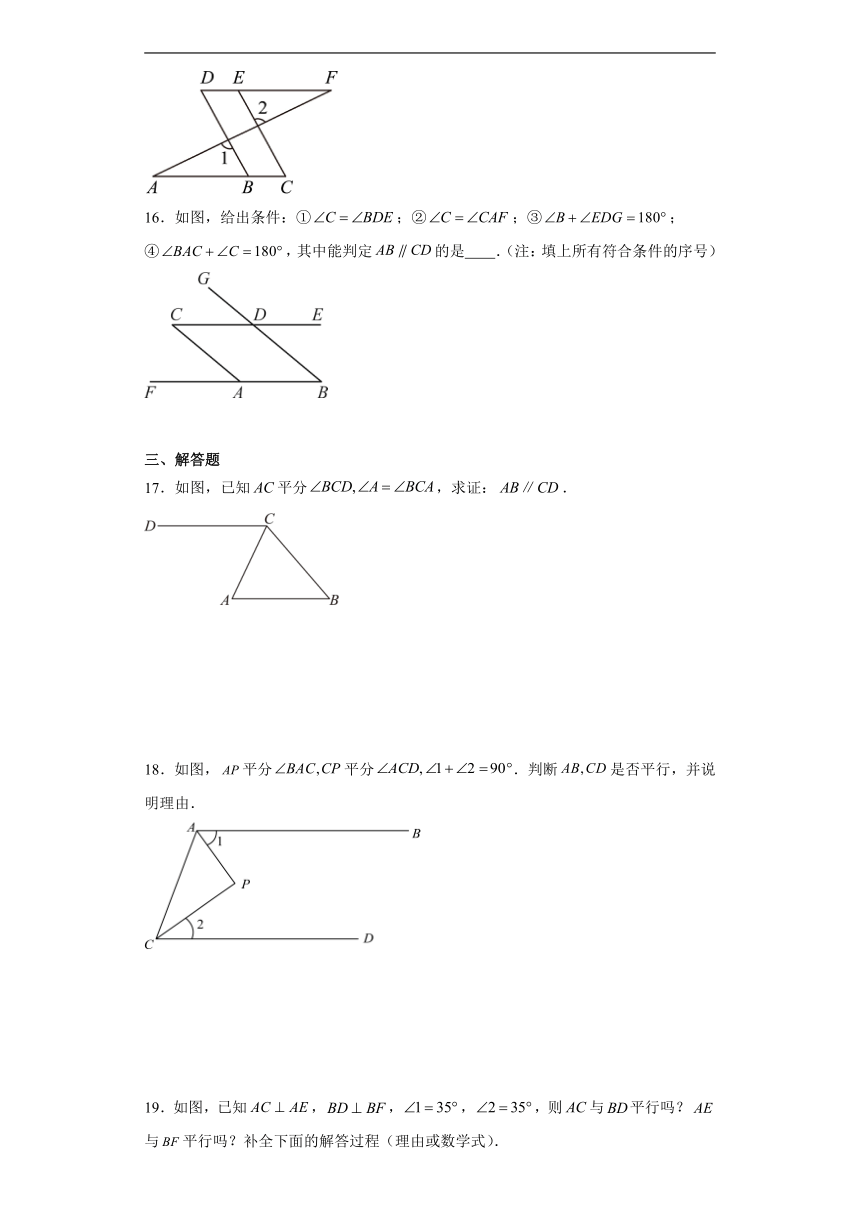
16.如图,给出条件:①;②;③;④,其中能判定的是 .(注:填上所有符合条件的序号)
三、解答题
17.如图,已知平分,求证:.
18.如图,平分平分.判断是否平行,并说明理由.
19.如图,已知,,,,则与平行吗?与平行吗?补全下面的解答过程(理由或数学式).
解: ( )
∴( ),
∴(同位角相等,两直线平行)
又∵( ),
,
∴(等式的性质),
同理可得,
∴(等量代换),
∴( ).
20.如图,如果,,那么与平行吗?说说你的理由.
参考答案:
1.A
【分析】本题考查了平行线公理的推论:平行于同一直线的两条直线平行.根据此性质即可判断.
【详解】解:若,则或b,c重合;
故选:A.
2.C
【分析】本题考查平行的判定定理,掌握平行的判定定理“判定方法1:同位角相等,两直线平行;判定方法2:内错角相等,两直线平行;判定方法3:同旁内角互补,两直线平行.”即可解题.
【详解】解:根据平行的判定定理,
,
,
,
,
,
,
综上所述,所以A、B、D项不能判定,C项正确,
故选:C.
3.D
【分析】此题主要考查了平行线的判定.根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行可得答案.
【详解】解:A、当时,无法得到,不符合题意;
B、当时,无法得到,不合题意;
C、当时,无法得到,不合题意;
D、当时,可得,符合题意.
故选:D.
4.C
【分析】本题主要考查了平行线的判定,能根据图形准确找出同位角、内错角和同旁内角是解决问题的关键.结合图形分析两角的位置关系,根据平行线的判定方法逐项进行判断即可得到结论.
【详解】解:,
,
故A选项不符合题意;
,不能判定,
故B选项不符合题意;
,
,
故C选项符合题意;
,
,
故D选项不符合题意;
故选:C.
5.B
【分析】本题考查了平行线的判定,判定方法有:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.根据平行线的判定定理解答即可.
【详解】解:.,内角错相等,两直线平行可得,不能判断,故本选项不符合题意;
.,内角错相等,两直线平行可得,可以判断,故本选项符合题意;
.,内角错相等,两直线平行可得,不能判断,故本选项不符合题意;
.,根据同旁内角互补,两直线平行可得,不能判断,故本选项不符合题意;
故选:B.
6.C
【分析】根据平行线的判定定理:同位角相等,两直线平行.逐项分析判断选择即可.
【详解】解:A、由,,得出,根据“同位角相等,两直线平行”能判定,故不符合题意;
B、由,,得出,根据“同位角相等,两直线平行”能判定,故不符合题意;
C、,,则,根据同位角互补,不能判定,故符合题意;
D、,根据“同位角相等,两直线平行”能判定,故不符合题意.
故选:C.
【点睛】本题考查了平行线的判定,找出判定两直线平行的依据同位角相等,两直线平行是解题的关键.
7.B
【分析】可以从直线的截线所组成的“三线八角”图形入手进行判断.
【详解】解:A、∵,
∴,不能证明,不符合题意;
B、∵,
∴,符合题意;
C、∵,
∴,不能证明,不符合题意;
D、∵,
∴,不能证明,不符合题意;
故选:B.
【点睛】此题考查平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
8.B
【分析】根据平行线的判定即可求解.
【详解】解:①、可判断,而,①不能判定,故①不符合题意;
②、由可得,故②符合题意;
③、由可得,故③不符合题意;
④、由可得,故④符合题意;
⑤、由可得,故⑤符合题意,
故选B.
【点睛】本题考查了平行线的判定,熟练掌握其判定定理是解题的关键.
9.(不唯一)
【分析】根据同旁内角互补两直线平行来解答即可,答案不唯一.
【详解】解:,
,
故答案为:(不唯一).
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键.
10.平行
【分析】根据角平分线的定义得出,再根据,得出,利用平行线的判定可得出两条直线平行.
【详解】解:∵平分,
∴,
∵,
∴,
∴,
故答案为:平行.
【点睛】本题考查了平行线的判定,解题关键是熟练运用内错角相等,两直线平行进行推理证明.
11.25
【分析】要使,则,根据已知条件即可确定旋转的度数.
【详解】解:当时,,
又,,
,
直线顺时针旋转的度数至少是,
故答案为:25.
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解题的关键.
12.内错角相等,两直线平行
【分析】由两个三角尺的形状、大小相同可得,由内错角相等,两直线平行可得,即可得到答案.
【详解】解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,熟练掌握内错角相等,两直线平行,是解题的关键.
13.(答案不唯一)
【分析】根据平行线的判定方法求解即可.
【详解】解:添加,根据内错角相等,两直线平行可判定;
也可添加,根据同旁内角互补,两直线平行可判定,
故答案为:(答案不唯一).
【点睛】本题考查平行线的判定,熟练掌握平行线的判定方法是解答的关键.
14.同位角相等,两直线平行
【分析】根据同位角相等,两直线平行解答即可.
【详解】如图,由作法可知,
∴(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行
【点睛】本题考查了平行线的作法,熟练掌握同位角相等,两直线平行是解答本题的关键.
15. 同位角相等,两直线平行
【分析】根据平行线的判定方法进行解答即可.
【详解】解:∵,,
∴,
∴(同位角相等,两直线平行).
故答案为:;;同位角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,解题的关键是熟练掌握平行线的判定方法,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
16.②③④
【分析】根据平行线的判定条件逐一判断即可.
【详解】解:由条件,可以通过同位角相等,两直线平行得到,不能得到,故①不符合题意;
由条件,可以通过内错角相等,两直线平行得到,故②符合题意;
由条件,可以通过同旁内角互补,两直线平行得到,故③符合题意;
由条件,可以通过同旁内角互补,两直线平行得到,故②符合题意;
故答案为:②③④.
【点睛】本题主要考查了平行线的判定,熟知平行线的判定条件是解题的关键.
17.见解析
【分析】本题主要考查的是平行线的判定,角平分线的定义,证明,最后再利用内错角相等,两直线平行即可证明.
【详解】证明:平分,
.
又,
.
.
18.,理由见解析
【分析】本题主要考查了角平分线的性质,平行线的判定,熟练掌握相关定理是证明的关键.先根据角平分线的性质得出,,再由可得,从而可得出结论.
【详解】解:,理由如下:
∵平分平分,
∴,,
∵,
∴,
∴.
19.详见解析
【分析】本题考查了平行线的判定,熟练掌握平行线的判定方法是解答本题的关键.由可证,证明可证.
【详解】解:∵(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
又∵(已知),
,
∴(等式的性质),
同理可得,
∴(等量代换),
∴(同位角相等,两直线平行).
20.,理由见详解
【分析】本题考查平行线的判定:内错角相等,两直线平行;同旁内角互补,两直线平行;平行于同一条直线的两直线平行,由此即可证明问题.
【详解】解:,理由如下:
.
一、单选题
1.在同一平面内,若,则b与c的关系为( )
A.平行或重合 B.平行或垂直 C.垂直 D.相交
2.如图,下面能判断的条件是( )
A. B. C. D.
3.下列条件能判定的是( )
A. B. C. D.
4.如图,下列条件中,能判断的是( )
A. B.
C. D.
5.如图,点 E 在 的延长线上,下列条件中能判断的是( )
A. B. C. D.
6.如图,下列条件中不能判断的是( )
A. B. C. D.
7.如图,在下列给出的条件中,能判定的是( )
A. B. C. D.
8.如图所示,以下5个条件:①;②;③;④;⑤.其中一定能判定的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.如图,点是延长线上一点,请添加一个你认为恰当的条件 ,使.
10.如图,,平分,则与的位置关系是 .
11.如图,直线与相交,,,要使直线与平行,则直线绕点顺时针旋转的角度至少是 °.
12.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
13.如图,不添加辅助线﹐请写出一个能判定的条件: .
14.如图,给出了过已知直线外一点,作已知直线的平行线的方法,其依据是 .
15.如图,已知点A,B,C和点D,E,F分别在同一直线上,,那么可以最终推出 ∥ ,判定平行的理由是 .
16.如图,给出条件:①;②;③;④,其中能判定的是 .(注:填上所有符合条件的序号)
三、解答题
17.如图,已知平分,求证:.
18.如图,平分平分.判断是否平行,并说明理由.
19.如图,已知,,,,则与平行吗?与平行吗?补全下面的解答过程(理由或数学式).
解: ( )
∴( ),
∴(同位角相等,两直线平行)
又∵( ),
,
∴(等式的性质),
同理可得,
∴(等量代换),
∴( ).
20.如图,如果,,那么与平行吗?说说你的理由.
参考答案:
1.A
【分析】本题考查了平行线公理的推论:平行于同一直线的两条直线平行.根据此性质即可判断.
【详解】解:若,则或b,c重合;
故选:A.
2.C
【分析】本题考查平行的判定定理,掌握平行的判定定理“判定方法1:同位角相等,两直线平行;判定方法2:内错角相等,两直线平行;判定方法3:同旁内角互补,两直线平行.”即可解题.
【详解】解:根据平行的判定定理,
,
,
,
,
,
,
综上所述,所以A、B、D项不能判定,C项正确,
故选:C.
3.D
【分析】此题主要考查了平行线的判定.根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行可得答案.
【详解】解:A、当时,无法得到,不符合题意;
B、当时,无法得到,不合题意;
C、当时,无法得到,不合题意;
D、当时,可得,符合题意.
故选:D.
4.C
【分析】本题主要考查了平行线的判定,能根据图形准确找出同位角、内错角和同旁内角是解决问题的关键.结合图形分析两角的位置关系,根据平行线的判定方法逐项进行判断即可得到结论.
【详解】解:,
,
故A选项不符合题意;
,不能判定,
故B选项不符合题意;
,
,
故C选项符合题意;
,
,
故D选项不符合题意;
故选:C.
5.B
【分析】本题考查了平行线的判定,判定方法有:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.根据平行线的判定定理解答即可.
【详解】解:.,内角错相等,两直线平行可得,不能判断,故本选项不符合题意;
.,内角错相等,两直线平行可得,可以判断,故本选项符合题意;
.,内角错相等,两直线平行可得,不能判断,故本选项不符合题意;
.,根据同旁内角互补,两直线平行可得,不能判断,故本选项不符合题意;
故选:B.
6.C
【分析】根据平行线的判定定理:同位角相等,两直线平行.逐项分析判断选择即可.
【详解】解:A、由,,得出,根据“同位角相等,两直线平行”能判定,故不符合题意;
B、由,,得出,根据“同位角相等,两直线平行”能判定,故不符合题意;
C、,,则,根据同位角互补,不能判定,故符合题意;
D、,根据“同位角相等,两直线平行”能判定,故不符合题意.
故选:C.
【点睛】本题考查了平行线的判定,找出判定两直线平行的依据同位角相等,两直线平行是解题的关键.
7.B
【分析】可以从直线的截线所组成的“三线八角”图形入手进行判断.
【详解】解:A、∵,
∴,不能证明,不符合题意;
B、∵,
∴,符合题意;
C、∵,
∴,不能证明,不符合题意;
D、∵,
∴,不能证明,不符合题意;
故选:B.
【点睛】此题考查平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
8.B
【分析】根据平行线的判定即可求解.
【详解】解:①、可判断,而,①不能判定,故①不符合题意;
②、由可得,故②符合题意;
③、由可得,故③不符合题意;
④、由可得,故④符合题意;
⑤、由可得,故⑤符合题意,
故选B.
【点睛】本题考查了平行线的判定,熟练掌握其判定定理是解题的关键.
9.(不唯一)
【分析】根据同旁内角互补两直线平行来解答即可,答案不唯一.
【详解】解:,
,
故答案为:(不唯一).
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键.
10.平行
【分析】根据角平分线的定义得出,再根据,得出,利用平行线的判定可得出两条直线平行.
【详解】解:∵平分,
∴,
∵,
∴,
∴,
故答案为:平行.
【点睛】本题考查了平行线的判定,解题关键是熟练运用内错角相等,两直线平行进行推理证明.
11.25
【分析】要使,则,根据已知条件即可确定旋转的度数.
【详解】解:当时,,
又,,
,
直线顺时针旋转的度数至少是,
故答案为:25.
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解题的关键.
12.内错角相等,两直线平行
【分析】由两个三角尺的形状、大小相同可得,由内错角相等,两直线平行可得,即可得到答案.
【详解】解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,熟练掌握内错角相等,两直线平行,是解题的关键.
13.(答案不唯一)
【分析】根据平行线的判定方法求解即可.
【详解】解:添加,根据内错角相等,两直线平行可判定;
也可添加,根据同旁内角互补,两直线平行可判定,
故答案为:(答案不唯一).
【点睛】本题考查平行线的判定,熟练掌握平行线的判定方法是解答的关键.
14.同位角相等,两直线平行
【分析】根据同位角相等,两直线平行解答即可.
【详解】如图,由作法可知,
∴(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行
【点睛】本题考查了平行线的作法,熟练掌握同位角相等,两直线平行是解答本题的关键.
15. 同位角相等,两直线平行
【分析】根据平行线的判定方法进行解答即可.
【详解】解:∵,,
∴,
∴(同位角相等,两直线平行).
故答案为:;;同位角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,解题的关键是熟练掌握平行线的判定方法,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
16.②③④
【分析】根据平行线的判定条件逐一判断即可.
【详解】解:由条件,可以通过同位角相等,两直线平行得到,不能得到,故①不符合题意;
由条件,可以通过内错角相等,两直线平行得到,故②符合题意;
由条件,可以通过同旁内角互补,两直线平行得到,故③符合题意;
由条件,可以通过同旁内角互补,两直线平行得到,故②符合题意;
故答案为:②③④.
【点睛】本题主要考查了平行线的判定,熟知平行线的判定条件是解题的关键.
17.见解析
【分析】本题主要考查的是平行线的判定,角平分线的定义,证明,最后再利用内错角相等,两直线平行即可证明.
【详解】证明:平分,
.
又,
.
.
18.,理由见解析
【分析】本题主要考查了角平分线的性质,平行线的判定,熟练掌握相关定理是证明的关键.先根据角平分线的性质得出,,再由可得,从而可得出结论.
【详解】解:,理由如下:
∵平分平分,
∴,,
∵,
∴,
∴.
19.详见解析
【分析】本题考查了平行线的判定,熟练掌握平行线的判定方法是解答本题的关键.由可证,证明可证.
【详解】解:∵(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
又∵(已知),
,
∴(等式的性质),
同理可得,
∴(等量代换),
∴(同位角相等,两直线平行).
20.,理由见详解
【分析】本题考查平行线的判定:内错角相等,两直线平行;同旁内角互补,两直线平行;平行于同一条直线的两直线平行,由此即可证明问题.
【详解】解:,理由如下:
.
