2023-2024学年初中数学湘教版八年级下册第1章 直角三角形 复习课学案(含答案)
文档属性
| 名称 | 2023-2024学年初中数学湘教版八年级下册第1章 直角三角形 复习课学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 22:57:50 | ||
图片预览




文档简介
第1章 直角三角形 复习课
复习目标
1.全面准确把握本章的知识体系.
2.综合直角三角形性质与判定全面解决实际问题.
3.能利用勾股定理及其逆定理解决直角三角形中求相关线段长度问题.
4.角平分线性质定理及其逆定理的综合应用.
◎重点:直角三角形的性质和判定,勾股定理及其逆定理,角平分线性质与判定在解决实际问题中的作用.
预习导学
体系建构
请你画出本章知识结构图,然后与下图对照比较.
【答案】互余 中线 互余 “SAS” “ASA” “AAS” “SSS” “HL” 相等
核心梳理
1.直角三角形的性质:
(1)直角三角形两个锐角 ;
(2)直角三角形斜边上的中线等于 ;
(3)在直角三角形中,30°角所对的直角边等于 ;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为 ;
(5)勾股定理:直角三角形两直角边a,b的平方和,等于斜边c的平方,即 .
2.直角三角形的判定方法:
(1)有一个角是 的三角形是直角三角形;
(2)有两个角 的三角形是直角三角形;
(3)勾股定理的逆定理:如果 ,那么以a,b,c为边的三角形是以c为斜边的直角三角形.
3.直角三角形全等的判定方法: 、 、 、 、 .
4.角平分线的性质定理:角平分线上的点到角两边的距离 .
5.角平分线的性质定理的逆定理:角的内部到角的两边距离相等的点在 上.
【答案】1.(1)互余
(2)斜边的一半
(3)斜边的一半
(4)30°
(5)a2+b2=c2
2.(1)直角
(2)互余
(3)a2+b2=c2
3.SAS ASA AAS SSS HL
4.相等
5.角的平分线
合作探究
专题一 直角三角形的性质
1.如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P.
(1)求∠APD的度数.
(2)若∠BDC=58°,求∠BAP的度数.
【答案】1.解:(1)∵∠C=90°,∴∠ABC+∠BAC=90°,
∴(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠BAP+∠ABP=∠BAC+∠ABC=(∠BAC+∠ABC)=45°,
∴∠APD=∠BAP+∠ABP=45°.
(2)∵∠BDC=58°,∴∠DBC=90°-∠BDC=32°.
∵BD平分∠ABC,∴∠ABD=∠DBC=32°,∴∠BAP=∠APD-∠ABD=45°-32°=13°.
专题二 勾股定理及其逆定理
2.如图,在正方形ABCD中,E是BC上一点,且BC∶EC=4∶1,F是DC的中点.
(1)判断△AEF的形状,并说明理由.
(2)若正方形的边长为4,求△AEF的面积.
【答案】2.解:(1)△AEF是直角三角形.理由如下:设正方形的边长为4a,∵F是DC的中点,∴DF=CF=2a,∵BC∶EC=4∶1,∴EC=a,BE=4a-a=3a.
在Rt△ADF中,AF2=(4a)2+(2a)2=20a2,在Rt△ECF中,EF2=(2a)2+a2=5a2,在Rt△ABE中,AE2=(4a)2+(3a)2=25a2,∴AF2+EF2=AE2,∴△AEF是直角三角形.
(2)正方形的边长为4时,4a=4,a=1,AF==2,EF=,△AEF的面积=AF·EF=×2×=5.
方法归纳交流 本题综合运用 定理及其 定理,合理地用正方形的边长表示出△AEF的各边的 是解决本题的关键.
【答案】勾股 逆 平方
专题三 勾股数
3.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五.”观察下列勾股数:3,4,5;5,12,13;7,24,25;….这类勾股数的特点是勾为奇数,弦与股相差1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
【答案】3.m2+1
专题四 直角三角形全等
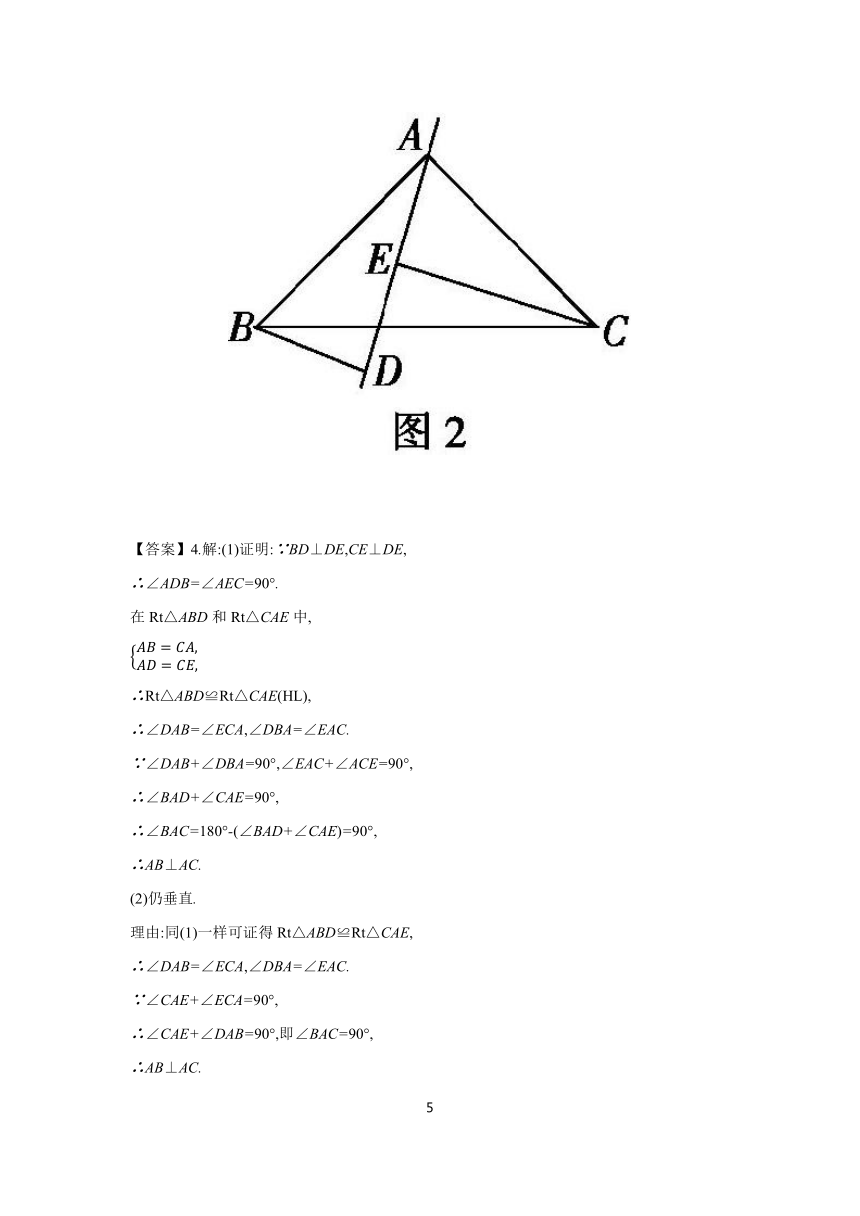
4.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E.
(1)如图1,若B,C在DE的同侧且AD=CE.求证:AB⊥AC.
(2)如图2,若B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗 若是,请给出证明;若不是,请说明理由.
【答案】4.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∴Rt△ABD≌Rt△CAE(HL),
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-(∠BAD+∠CAE)=90°,
∴AB⊥AC.
(2)仍垂直.
理由:同(1)一样可证得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠CAE+∠ECA=90°,
∴∠CAE+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
专题五 角平分线的性质定理与逆定理
5.如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形.
(2)判断点O是否在∠BAC的平分线上,并说明理由.
6.如图,在△ABC中,D是AB边上的一点,且AC=AD.
(1)请用无刻度的直尺和圆规作出∠CAB的平分线AM,交BC于点M.(保留作图痕迹,不写作法,标明字母)
(2)在(1)的条件下,连接DM,试猜想CM与DM的数量关系,并证明你的猜想.
7.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G,请猜测AE与FG之间有怎样的数量关系,并说明理由.
【答案】5.解:(1)证明:∵OB=OC,∴∠OBC=∠OCB.∵锐角△ABC的两条高BD、CE相交于点O,∴∠BEC=∠BDC=90°,
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC+∠ACB=180°,∴∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
(2)如图,连接AO并延长交BC于点F,∵AB=AC,OB=OC,AO=AO,∴△ABO≌△ACO,
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
6.解:(1)如图,AM为所求.
(2)CM=DM.
证明:如图,连接DM.∵AM是∠CAB的平分线,
∴∠BAM=∠CAM.
在△MAC和△MAD中,
∴△MAC≌△MAD(SAS),
∴CM=DM.
7.解:AE=FG.
理由:∵CF平分∠ACB,FA⊥AC,FG⊥BC,
∴FG=FA,∵∠AFC+∠ACF=90°,∠DEC+∠ECD=90°,且∠ACF=∠ECD,∴∠AFC=∠DEC,∵∠AEF=∠DEC,∴∠AFC=∠AEF,∴AE=FA,∴AE=FG.
专题六 直角三角形性质的综合应用
8.乐乐在学习中遇到了这样的问题:
在如图所示的三角形纸片ABC中,∠C=90°,AC=3,BC=4,将△ABC沿某一条直线剪开,使其变成两个三角形,且要求其中的一个三角形是等腰三角形,你有几种方法呢
经过思考,乐乐发现要想沿一条直线把三角形分割成两个三角形,这条直线需要经过三角形的某个定点,请你帮助乐乐写出当这条直线经过定点点A时,剪出的等腰三角形的面积是 .
9.如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心,50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离.
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
【答案】8.4.5或
9.解:(1)如图,过点A作AD⊥ON于点D,∵∠NOM=30°,AO=80米,∴AD=40米,即对学校A的噪声影响最大时卡车P与学校A的距离为40米.
(2)由图可知,以点A为圆心,以50米长为半径画圆,分别交ON于B,C两点,AD⊥BC于点D,BD=CD=BC,OA=80米.∵在Rt△AOD中,∠AOB=30°,∴AD=OA=×80=40(米),在Rt△ABD中,AB=50,AD=40,由勾股定理得BD===30(米),故BC=2×30=60(米),即重型运输卡车在经过BC时对学校产生影响.∵重型运输卡车的速度为18千米/小时,即=300(米/分钟),∴重型运输卡车经过BC时需要60÷300=0.2(分钟).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为0.2分钟.
专题七 与直角三角形有关的阅读理解题
10.(没有直角尺也能作出直角)阅读与思考
下图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如图1所示的四边形木板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢 办法一:如图1,可利用一把有刻度的直尺在AB上量出CD=30 cm,然后分别以D,C为圆心,以50 cm与40 cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°. 办法二:如图2,可以取一根笔直的木棒,用铅笔在木棒上点出M,N两点,然后把木棒斜放在木板上,使点M与点C重合,用铅笔在木板上将点N对应的位置标记为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS=90°.
续表
我有如下思考:以上两种办法依据的是什么数学原理呢 我还有什么办法不用直角尺也能作出垂线呢 …
任务:
(1)填空:“办法一”依据的一个数学定理是 .
(2)根据“办法二”的操作过程,证明∠RCS=90°.
(3)①尺规作图:请在图3的木板上,过点C作出AB的垂线(在木板上保留作图痕迹,不写作法).
②说明你的作法所依据的数学定理或基本事实.(写出一个即可)
【答案】10.解:(1)勾股定理的逆定理.
提示:∵CD=30,DE=50,CE=40,
∴CD2+CE2=302+402=502=DE2,
∴∠DCE=90°.
故“办法一”依据的一个数学定理是勾股定理的逆定理.
(2)证明:由作图方法可知,QR=QC,QS=QC,
∴∠QCR=∠QRC,∠QCS=∠QSC.
∵∠SRC+∠QCS+∠QCR+∠QSC=180°,
∴2(∠QCR+∠QCS)=180°,
∴∠QCR+∠QCS=90°,
即∠RCS=90°.
(3)①如图所示,直线PC即为所求.
②(答案不唯一)到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
2
复习目标
1.全面准确把握本章的知识体系.
2.综合直角三角形性质与判定全面解决实际问题.
3.能利用勾股定理及其逆定理解决直角三角形中求相关线段长度问题.
4.角平分线性质定理及其逆定理的综合应用.
◎重点:直角三角形的性质和判定,勾股定理及其逆定理,角平分线性质与判定在解决实际问题中的作用.
预习导学
体系建构
请你画出本章知识结构图,然后与下图对照比较.
【答案】互余 中线 互余 “SAS” “ASA” “AAS” “SSS” “HL” 相等
核心梳理
1.直角三角形的性质:
(1)直角三角形两个锐角 ;
(2)直角三角形斜边上的中线等于 ;
(3)在直角三角形中,30°角所对的直角边等于 ;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为 ;
(5)勾股定理:直角三角形两直角边a,b的平方和,等于斜边c的平方,即 .
2.直角三角形的判定方法:
(1)有一个角是 的三角形是直角三角形;
(2)有两个角 的三角形是直角三角形;
(3)勾股定理的逆定理:如果 ,那么以a,b,c为边的三角形是以c为斜边的直角三角形.
3.直角三角形全等的判定方法: 、 、 、 、 .
4.角平分线的性质定理:角平分线上的点到角两边的距离 .
5.角平分线的性质定理的逆定理:角的内部到角的两边距离相等的点在 上.
【答案】1.(1)互余
(2)斜边的一半
(3)斜边的一半
(4)30°
(5)a2+b2=c2
2.(1)直角
(2)互余
(3)a2+b2=c2
3.SAS ASA AAS SSS HL
4.相等
5.角的平分线
合作探究
专题一 直角三角形的性质
1.如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P.
(1)求∠APD的度数.
(2)若∠BDC=58°,求∠BAP的度数.
【答案】1.解:(1)∵∠C=90°,∴∠ABC+∠BAC=90°,
∴(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠BAP+∠ABP=∠BAC+∠ABC=(∠BAC+∠ABC)=45°,
∴∠APD=∠BAP+∠ABP=45°.
(2)∵∠BDC=58°,∴∠DBC=90°-∠BDC=32°.
∵BD平分∠ABC,∴∠ABD=∠DBC=32°,∴∠BAP=∠APD-∠ABD=45°-32°=13°.
专题二 勾股定理及其逆定理
2.如图,在正方形ABCD中,E是BC上一点,且BC∶EC=4∶1,F是DC的中点.
(1)判断△AEF的形状,并说明理由.
(2)若正方形的边长为4,求△AEF的面积.
【答案】2.解:(1)△AEF是直角三角形.理由如下:设正方形的边长为4a,∵F是DC的中点,∴DF=CF=2a,∵BC∶EC=4∶1,∴EC=a,BE=4a-a=3a.
在Rt△ADF中,AF2=(4a)2+(2a)2=20a2,在Rt△ECF中,EF2=(2a)2+a2=5a2,在Rt△ABE中,AE2=(4a)2+(3a)2=25a2,∴AF2+EF2=AE2,∴△AEF是直角三角形.
(2)正方形的边长为4时,4a=4,a=1,AF==2,EF=,△AEF的面积=AF·EF=×2×=5.
方法归纳交流 本题综合运用 定理及其 定理,合理地用正方形的边长表示出△AEF的各边的 是解决本题的关键.
【答案】勾股 逆 平方
专题三 勾股数
3.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五.”观察下列勾股数:3,4,5;5,12,13;7,24,25;….这类勾股数的特点是勾为奇数,弦与股相差1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
【答案】3.m2+1
专题四 直角三角形全等
4.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E.
(1)如图1,若B,C在DE的同侧且AD=CE.求证:AB⊥AC.
(2)如图2,若B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗 若是,请给出证明;若不是,请说明理由.
【答案】4.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
在Rt△ABD和Rt△CAE中,
∴Rt△ABD≌Rt△CAE(HL),
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°,
∴∠BAC=180°-(∠BAD+∠CAE)=90°,
∴AB⊥AC.
(2)仍垂直.
理由:同(1)一样可证得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠CAE+∠ECA=90°,
∴∠CAE+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
专题五 角平分线的性质定理与逆定理
5.如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形.
(2)判断点O是否在∠BAC的平分线上,并说明理由.
6.如图,在△ABC中,D是AB边上的一点,且AC=AD.
(1)请用无刻度的直尺和圆规作出∠CAB的平分线AM,交BC于点M.(保留作图痕迹,不写作法,标明字母)
(2)在(1)的条件下,连接DM,试猜想CM与DM的数量关系,并证明你的猜想.
7.如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G,请猜测AE与FG之间有怎样的数量关系,并说明理由.
【答案】5.解:(1)证明:∵OB=OC,∴∠OBC=∠OCB.∵锐角△ABC的两条高BD、CE相交于点O,∴∠BEC=∠BDC=90°,
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC+∠ACB=180°,∴∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
(2)如图,连接AO并延长交BC于点F,∵AB=AC,OB=OC,AO=AO,∴△ABO≌△ACO,
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
6.解:(1)如图,AM为所求.
(2)CM=DM.
证明:如图,连接DM.∵AM是∠CAB的平分线,
∴∠BAM=∠CAM.
在△MAC和△MAD中,
∴△MAC≌△MAD(SAS),
∴CM=DM.
7.解:AE=FG.
理由:∵CF平分∠ACB,FA⊥AC,FG⊥BC,
∴FG=FA,∵∠AFC+∠ACF=90°,∠DEC+∠ECD=90°,且∠ACF=∠ECD,∴∠AFC=∠DEC,∵∠AEF=∠DEC,∴∠AFC=∠AEF,∴AE=FA,∴AE=FG.
专题六 直角三角形性质的综合应用
8.乐乐在学习中遇到了这样的问题:
在如图所示的三角形纸片ABC中,∠C=90°,AC=3,BC=4,将△ABC沿某一条直线剪开,使其变成两个三角形,且要求其中的一个三角形是等腰三角形,你有几种方法呢
经过思考,乐乐发现要想沿一条直线把三角形分割成两个三角形,这条直线需要经过三角形的某个定点,请你帮助乐乐写出当这条直线经过定点点A时,剪出的等腰三角形的面积是 .
9.如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心,50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离.
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
【答案】8.4.5或
9.解:(1)如图,过点A作AD⊥ON于点D,∵∠NOM=30°,AO=80米,∴AD=40米,即对学校A的噪声影响最大时卡车P与学校A的距离为40米.
(2)由图可知,以点A为圆心,以50米长为半径画圆,分别交ON于B,C两点,AD⊥BC于点D,BD=CD=BC,OA=80米.∵在Rt△AOD中,∠AOB=30°,∴AD=OA=×80=40(米),在Rt△ABD中,AB=50,AD=40,由勾股定理得BD===30(米),故BC=2×30=60(米),即重型运输卡车在经过BC时对学校产生影响.∵重型运输卡车的速度为18千米/小时,即=300(米/分钟),∴重型运输卡车经过BC时需要60÷300=0.2(分钟).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为0.2分钟.
专题七 与直角三角形有关的阅读理解题
10.(没有直角尺也能作出直角)阅读与思考
下图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日 没有直角尺也能作出直角 今天,我在书店一本书上看到下面材料:木工师傅有一块如图1所示的四边形木板,他已经在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢 办法一:如图1,可利用一把有刻度的直尺在AB上量出CD=30 cm,然后分别以D,C为圆心,以50 cm与40 cm为半径画圆弧,两弧相交于点E,作直线CE,则∠DCE必为90°. 办法二:如图2,可以取一根笔直的木棒,用铅笔在木棒上点出M,N两点,然后把木棒斜放在木板上,使点M与点C重合,用铅笔在木板上将点N对应的位置标记为点Q,保持点N不动,将木棒绕点N旋转,使点M落在AB上,在木板上将点M对应的位置标记为点R.然后将RQ延长,在延长线上截取线段QS=MN,得到点S,作直线SC,则∠RCS=90°.
续表
我有如下思考:以上两种办法依据的是什么数学原理呢 我还有什么办法不用直角尺也能作出垂线呢 …
任务:
(1)填空:“办法一”依据的一个数学定理是 .
(2)根据“办法二”的操作过程,证明∠RCS=90°.
(3)①尺规作图:请在图3的木板上,过点C作出AB的垂线(在木板上保留作图痕迹,不写作法).
②说明你的作法所依据的数学定理或基本事实.(写出一个即可)
【答案】10.解:(1)勾股定理的逆定理.
提示:∵CD=30,DE=50,CE=40,
∴CD2+CE2=302+402=502=DE2,
∴∠DCE=90°.
故“办法一”依据的一个数学定理是勾股定理的逆定理.
(2)证明:由作图方法可知,QR=QC,QS=QC,
∴∠QCR=∠QRC,∠QCS=∠QSC.
∵∠SRC+∠QCS+∠QCR+∠QSC=180°,
∴2(∠QCR+∠QCS)=180°,
∴∠QCR+∠QCS=90°,
即∠RCS=90°.
(3)①如图所示,直线PC即为所求.
②(答案不唯一)到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
