第2章 四边形 复习课 学案(含答案) 2023-2024学年初中数学湘教版八年级下册
文档属性
| 名称 | 第2章 四边形 复习课 学案(含答案) 2023-2024学年初中数学湘教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 253.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览




文档简介
第2章 四边形 复习课
复习目标
1.会计算多边形的内角和与外角和,知道正多边形的概念.
2.理解中心对称的概念,知道所有平行四边形都是中心对称图形.
3.梳理平行四边形、矩形、菱形、正方形的性质和判定.
4.掌握中位线定理和直角三角形的性质定理.
◎重点:特殊平行四边形的性质与判定.
预习导学
体系建构
核心梳理
1.多边形
(1)n边形的内角和等于 ;任意多边形的外角和等于 .
(2)在平面内,边相等、角也都相等的多边形叫做 .
2.图形变换——中心对称
(1)如果一个图形绕点O旋转 ,得到的像与另一个图形重合,那么称这两个图形关于点O ,点O叫做 .成中心对称的两个图形中,对应点的连线经过 ,且被对称中心 .
(2)如果一个图形绕一个点O旋转 ,所得到的像与原来的图形相互重合,那么这个图形叫做中心对称图形,这个点O叫做它的 .
(3)平行四边形是 , 是它的对称中心.
3.平行四边形
(1)定义:两组对边分别 的四边形叫做平行四边形.
(2)性质:对边分别 ,对角分别 ,对角线 .
(3)判定:两组对边分别 的四边形是平行四边形;两组对角分别 的四边形是平行四边形;对角线相互 的四边形是平行四边形;一组对边 的四边形是平行四边形.
(4)推理性质:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这 ;三角形的中位线 于三角形的第三边,并且等于第三边的一半.
4.矩形
(1)定义:有一个角是 的平行四边形叫做矩形.
(2)性质:矩形具有平行四边形的所有性质,此外,矩形的四个角都是 ;矩形的对角线 .
(3)判定:对角线相等的 是矩形;有三个角是 的四边形是矩形.
(4)推理得直角三角形的性质:直角三角形斜边上的中线等于 .
5.菱形
(1)定义:有一组邻边 的平行四边形叫做菱形.
(2)性质:菱形具有平行四边形的所有性质,此外,菱形的四条边都 ;菱形的两条对角线 ,并且每一条对角线平分一组 .
(3)判定:对角线互相 的平行四边形是菱形;四条边 的四边形是菱形.
(4)面积为 的一半.
6.正方形
(1)定义:有 相等且有一个角是 的平行四边形叫做正方形.
(2)性质:正方形具有平行四边形的所有性质;正方形具有 和 的所有性质.
(3)判定:既是 ,又是 的四边形是正方形.
【答案】1.(1)(n-2)·180° 360°
(2)正多边形
2.(1)180° 中心对称 对称中心 对称中心 平分
(2)180° 对称中心
(3)中心对称图形 对角线的交点
3.(1)平行
(2)相等 相等 相互平分
(3)相等 相等 平分 平行且相等
(4)两条平行线之间的距离 平行
4.(1)直角
(2)直角 相等
(3)平行四边形 直角
(4)斜边的一半
5.(1)相等
(2)相等 互相垂直 对角
(3)垂直 相等
(4)两条对角线长的乘积
6.(1)一组邻边 直角
(2)矩形 菱形
(3)矩形 菱形
合作探究
专题一 多边形的内角和与外角和
1.如图,在△ABC中,∠B=50°,若沿图中虚线剪去∠B,则∠1+∠2等于 ( )
A.130° B.230°
C.270° D.310°
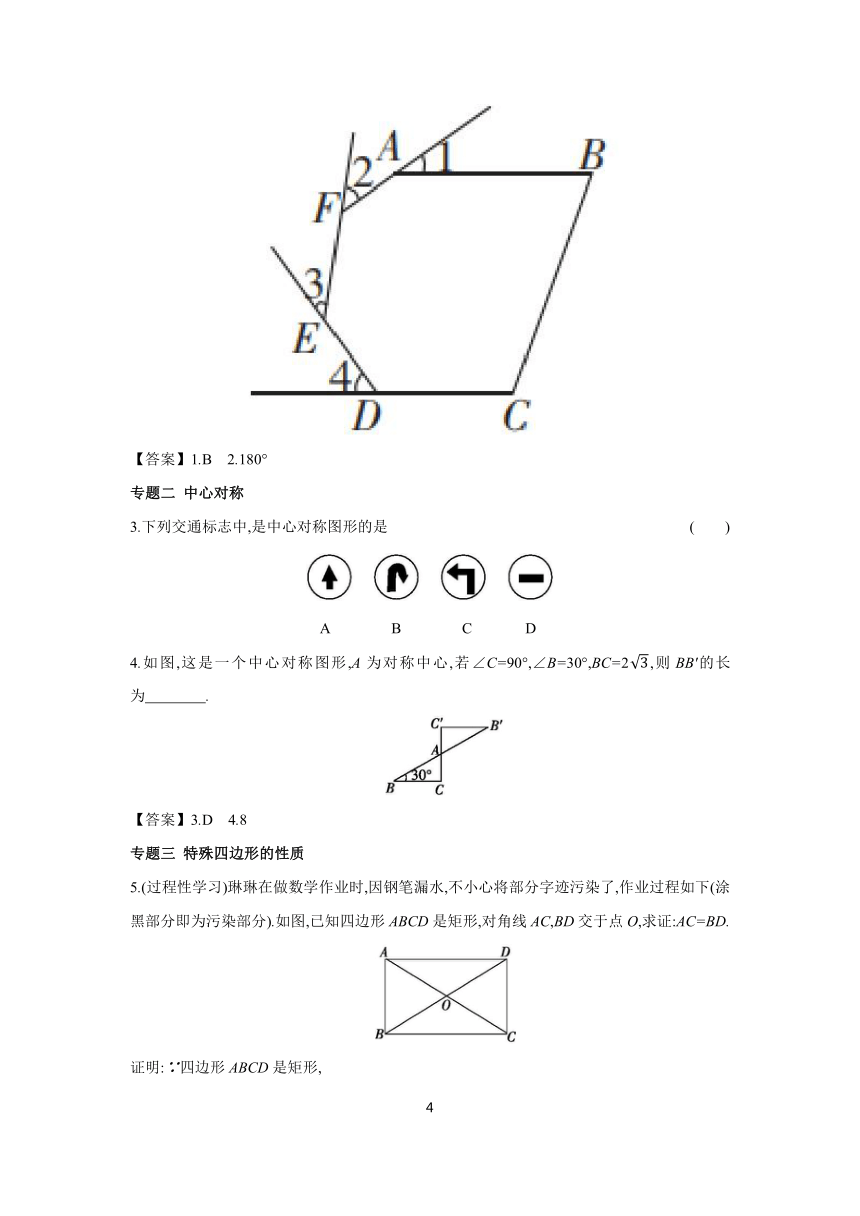
2.如图,在六边形ABCDEF中,AB∥CD,∠1,∠2,∠3,∠4分别是∠BAF,∠AFE,∠FED,∠EDC的外角,则∠1+∠2+∠3+∠4= .
【答案】1.B 2.180°
专题二 中心对称
3.下列交通标志中,是中心对称图形的是 ( )
A B C D
4.如图,这是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB'的长为 .
【答案】3.D 4.8
专题三 特殊四边形的性质
5.(过程性学习)琳琳在做数学作业时,因钢笔漏水,不小心将部分字迹污染了,作业过程如下(涂黑部分即为污染部分).如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,求证:AC=BD.
证明:∵四边形ABCD是矩形,
∴①,∠ABC=∠DCB=90°.
又∵②,
∴△ABC≌△DCB,
∴AC=BD.
污染部分的内容有以下四个选项供选择,a.AD=BC;b.AB=CD;c.AO=CO;d.BC=CB.则下列说法正确的是 ( )
A.①是a,②是d B.①是b,②是c
C.①是a,②是c D.①是b,②是d
6.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数是 ( )
A.45° B.22.5°
C.67.5° D.75°
7.如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是 .
【答案】5.D 6.B
7.24
专题四 特殊四边形的判定
8.下列说法:
①有一个角是直角的四边形是矩形.
②有一组邻边相等的平行四边形是菱形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
9.如图,菱形ABCD的对角线AC,BD相交于点O,在AC上截取OE=OF=OB,顺次连接B,F,D,E四点.求证:四边形BFDE是正方形.
10.如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形.
(2)求证:BD=MN.
【答案】8.B
9.证明:∵菱形ABCD的对角线AC,BD相交于点O,
∴AC⊥BD,OB=OD.
∵OE=OF=OB,
∴OE=OF=OB=OD,
∴四边形BFDE是矩形.
又∵BD⊥EF,∴四边形BFDE是正方形.
10.证明:(1)∵ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵M,N分别是AD,BC的中点,
∴MD=NC,MD∥NC,
∴MNCD是平行四边形.
(2)如图,连接ND.
∵MNCD是平行四边形,
∴MN=DC.
∵N是BC的中点,
∴BN=CN.
∵BC=2CD,∠C=60°,
∴△NCD是等边三角形,
∴ND=NC,∠DNC=60°.
∵∠DNC是△BND的外角,
∴∠NBD+∠NDB=∠DNC.
∵DN=NC=NB,
∴∠DBN=∠BDN=∠DNC=30°,
∴∠BDC=90°,
∴DB==CD=MN.
专题五 特殊四边形的性质与判定
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,AB=4,求四边形ABCD的面积.
12.如图,在Rt△ABC中,∠C=90°,延长CB至点D,使得BD=CB,过点A,D分别作AE∥BD,DE∥BA,AE与DE相交于点E.下面是两位同学的对话:
小星:根据题目的已知条件可知,若连接EB,则可证明EB⊥CD. 小红:根据题目的已知条件可知,若连接CE,则可证明CE=DE.
(1)请你选择一位同学的说法,并进行证明.
(2)连接AD,若AD=5,=,求AC的长.
【答案】11.解:(1)证明:∵△ACE是等边三角形,∴EA=EC.
∵四边形ABCD是平行四边形,
∴AO=OC,∴EO⊥AC,即BD⊥AC,
∴平行四边形ABCD是菱形.
(2)∵△ACE是等边三角形,∴∠EAC=60°.
由(1)知,EO⊥AC,AO=OC,
∴∠AEO=∠CEO=30°,△AOE是直角三角形,
∵∠AED=2∠EAD,
∴∠EAD=15°,∴∠ADO=∠AEO+∠EAD=45°,
∴∠ADC=2∠ADO=90°,
∴菱形ABCD是正方形,
∴四边形ABCD的面积=AB2=(4)2=80.
12.解:(1)证明:
小星:如图1,连接BE.
∵AE∥BD,DE∥BA,
∴四边形ABDE是平行四边形,
∴AE=BD.
∵BD=BC,∴AE=BC.
∵AE∥BC,∴四边形AEBC是平行四边形.
∵∠C=90°,∴平行四边形AEBC是矩形,
∴∠EBC=90°,∴EB⊥CD;
小红:如图2,连接CE,BE.
∵AE∥BD,DE∥BA,
∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE.
∵BD=BC,∴AE=BC.
∵AE∥BC,∴四边形AEBC是平行四边形.
∵∠C=90°,∴平行四边形AEBC是矩形,
∴AB=CE,∴DE=CE.
(2)如图3,连接AD.
∵=,∴设CB=2k,AC=3k,
∴CD=4k.
∵AC2+CD2=AD2,AD=5,
∴(3k)2+(4k)2=(5)2,
∴k=,∴AC=3.
专题六 四边形的折叠问题
13.如图,有一直角三角形纸片ABC,边BC=6,AB=10,∠ACB=90°,将该直角三角形纸片沿DE折叠,使点A与点C重合,则四边形DBCE的周长为 .
14.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2.
以上结论中,你认为正确的有 ( )
A.1个 B.2个 C.3个 D.4个
15.如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
(1)求证:△AOE≌△COD.
(2)若∠OCD=30°,AB=,求△AOC的面积.
【答案】13.18 14.C
15.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°.
∵矩形ABCD沿对角线AC折叠点B落在点E处,
∴AB=AE,∠B=∠E,
∴AE=CD,∠D=∠E.
在△AOE和△COD中,
∴△AOE≌△COD(AAS).
(2)∵△AOE≌△COD,
∴AO=CO.
∵∠OCD=30°,AB=,
∴CO= 2,
∴△AOC的面积=AO·CD=×2×=.
2
复习目标
1.会计算多边形的内角和与外角和,知道正多边形的概念.
2.理解中心对称的概念,知道所有平行四边形都是中心对称图形.
3.梳理平行四边形、矩形、菱形、正方形的性质和判定.
4.掌握中位线定理和直角三角形的性质定理.
◎重点:特殊平行四边形的性质与判定.
预习导学
体系建构
核心梳理
1.多边形
(1)n边形的内角和等于 ;任意多边形的外角和等于 .
(2)在平面内,边相等、角也都相等的多边形叫做 .
2.图形变换——中心对称
(1)如果一个图形绕点O旋转 ,得到的像与另一个图形重合,那么称这两个图形关于点O ,点O叫做 .成中心对称的两个图形中,对应点的连线经过 ,且被对称中心 .
(2)如果一个图形绕一个点O旋转 ,所得到的像与原来的图形相互重合,那么这个图形叫做中心对称图形,这个点O叫做它的 .
(3)平行四边形是 , 是它的对称中心.
3.平行四边形
(1)定义:两组对边分别 的四边形叫做平行四边形.
(2)性质:对边分别 ,对角分别 ,对角线 .
(3)判定:两组对边分别 的四边形是平行四边形;两组对角分别 的四边形是平行四边形;对角线相互 的四边形是平行四边形;一组对边 的四边形是平行四边形.
(4)推理性质:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这 ;三角形的中位线 于三角形的第三边,并且等于第三边的一半.
4.矩形
(1)定义:有一个角是 的平行四边形叫做矩形.
(2)性质:矩形具有平行四边形的所有性质,此外,矩形的四个角都是 ;矩形的对角线 .
(3)判定:对角线相等的 是矩形;有三个角是 的四边形是矩形.
(4)推理得直角三角形的性质:直角三角形斜边上的中线等于 .
5.菱形
(1)定义:有一组邻边 的平行四边形叫做菱形.
(2)性质:菱形具有平行四边形的所有性质,此外,菱形的四条边都 ;菱形的两条对角线 ,并且每一条对角线平分一组 .
(3)判定:对角线互相 的平行四边形是菱形;四条边 的四边形是菱形.
(4)面积为 的一半.
6.正方形
(1)定义:有 相等且有一个角是 的平行四边形叫做正方形.
(2)性质:正方形具有平行四边形的所有性质;正方形具有 和 的所有性质.
(3)判定:既是 ,又是 的四边形是正方形.
【答案】1.(1)(n-2)·180° 360°
(2)正多边形
2.(1)180° 中心对称 对称中心 对称中心 平分
(2)180° 对称中心
(3)中心对称图形 对角线的交点
3.(1)平行
(2)相等 相等 相互平分
(3)相等 相等 平分 平行且相等
(4)两条平行线之间的距离 平行
4.(1)直角
(2)直角 相等
(3)平行四边形 直角
(4)斜边的一半
5.(1)相等
(2)相等 互相垂直 对角
(3)垂直 相等
(4)两条对角线长的乘积
6.(1)一组邻边 直角
(2)矩形 菱形
(3)矩形 菱形
合作探究
专题一 多边形的内角和与外角和
1.如图,在△ABC中,∠B=50°,若沿图中虚线剪去∠B,则∠1+∠2等于 ( )
A.130° B.230°
C.270° D.310°
2.如图,在六边形ABCDEF中,AB∥CD,∠1,∠2,∠3,∠4分别是∠BAF,∠AFE,∠FED,∠EDC的外角,则∠1+∠2+∠3+∠4= .
【答案】1.B 2.180°
专题二 中心对称
3.下列交通标志中,是中心对称图形的是 ( )
A B C D
4.如图,这是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB'的长为 .
【答案】3.D 4.8
专题三 特殊四边形的性质
5.(过程性学习)琳琳在做数学作业时,因钢笔漏水,不小心将部分字迹污染了,作业过程如下(涂黑部分即为污染部分).如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,求证:AC=BD.
证明:∵四边形ABCD是矩形,
∴①,∠ABC=∠DCB=90°.
又∵②,
∴△ABC≌△DCB,
∴AC=BD.
污染部分的内容有以下四个选项供选择,a.AD=BC;b.AB=CD;c.AO=CO;d.BC=CB.则下列说法正确的是 ( )
A.①是a,②是d B.①是b,②是c
C.①是a,②是c D.①是b,②是d
6.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数是 ( )
A.45° B.22.5°
C.67.5° D.75°
7.如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是 .
【答案】5.D 6.B
7.24
专题四 特殊四边形的判定
8.下列说法:
①有一个角是直角的四边形是矩形.
②有一组邻边相等的平行四边形是菱形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
9.如图,菱形ABCD的对角线AC,BD相交于点O,在AC上截取OE=OF=OB,顺次连接B,F,D,E四点.求证:四边形BFDE是正方形.
10.如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形.
(2)求证:BD=MN.
【答案】8.B
9.证明:∵菱形ABCD的对角线AC,BD相交于点O,
∴AC⊥BD,OB=OD.
∵OE=OF=OB,
∴OE=OF=OB=OD,
∴四边形BFDE是矩形.
又∵BD⊥EF,∴四边形BFDE是正方形.
10.证明:(1)∵ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵M,N分别是AD,BC的中点,
∴MD=NC,MD∥NC,
∴MNCD是平行四边形.
(2)如图,连接ND.
∵MNCD是平行四边形,
∴MN=DC.
∵N是BC的中点,
∴BN=CN.
∵BC=2CD,∠C=60°,
∴△NCD是等边三角形,
∴ND=NC,∠DNC=60°.
∵∠DNC是△BND的外角,
∴∠NBD+∠NDB=∠DNC.
∵DN=NC=NB,
∴∠DBN=∠BDN=∠DNC=30°,
∴∠BDC=90°,
∴DB==CD=MN.
专题五 特殊四边形的性质与判定
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,AB=4,求四边形ABCD的面积.
12.如图,在Rt△ABC中,∠C=90°,延长CB至点D,使得BD=CB,过点A,D分别作AE∥BD,DE∥BA,AE与DE相交于点E.下面是两位同学的对话:
小星:根据题目的已知条件可知,若连接EB,则可证明EB⊥CD. 小红:根据题目的已知条件可知,若连接CE,则可证明CE=DE.
(1)请你选择一位同学的说法,并进行证明.
(2)连接AD,若AD=5,=,求AC的长.
【答案】11.解:(1)证明:∵△ACE是等边三角形,∴EA=EC.
∵四边形ABCD是平行四边形,
∴AO=OC,∴EO⊥AC,即BD⊥AC,
∴平行四边形ABCD是菱形.
(2)∵△ACE是等边三角形,∴∠EAC=60°.
由(1)知,EO⊥AC,AO=OC,
∴∠AEO=∠CEO=30°,△AOE是直角三角形,
∵∠AED=2∠EAD,
∴∠EAD=15°,∴∠ADO=∠AEO+∠EAD=45°,
∴∠ADC=2∠ADO=90°,
∴菱形ABCD是正方形,
∴四边形ABCD的面积=AB2=(4)2=80.
12.解:(1)证明:
小星:如图1,连接BE.
∵AE∥BD,DE∥BA,
∴四边形ABDE是平行四边形,
∴AE=BD.
∵BD=BC,∴AE=BC.
∵AE∥BC,∴四边形AEBC是平行四边形.
∵∠C=90°,∴平行四边形AEBC是矩形,
∴∠EBC=90°,∴EB⊥CD;
小红:如图2,连接CE,BE.
∵AE∥BD,DE∥BA,
∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE.
∵BD=BC,∴AE=BC.
∵AE∥BC,∴四边形AEBC是平行四边形.
∵∠C=90°,∴平行四边形AEBC是矩形,
∴AB=CE,∴DE=CE.
(2)如图3,连接AD.
∵=,∴设CB=2k,AC=3k,
∴CD=4k.
∵AC2+CD2=AD2,AD=5,
∴(3k)2+(4k)2=(5)2,
∴k=,∴AC=3.
专题六 四边形的折叠问题
13.如图,有一直角三角形纸片ABC,边BC=6,AB=10,∠ACB=90°,将该直角三角形纸片沿DE折叠,使点A与点C重合,则四边形DBCE的周长为 .
14.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2.
以上结论中,你认为正确的有 ( )
A.1个 B.2个 C.3个 D.4个
15.如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
(1)求证:△AOE≌△COD.
(2)若∠OCD=30°,AB=,求△AOC的面积.
【答案】13.18 14.C
15.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°.
∵矩形ABCD沿对角线AC折叠点B落在点E处,
∴AB=AE,∠B=∠E,
∴AE=CD,∠D=∠E.
在△AOE和△COD中,
∴△AOE≌△COD(AAS).
(2)∵△AOE≌△COD,
∴AO=CO.
∵∠OCD=30°,AB=,
∴CO= 2,
∴△AOC的面积=AO·CD=×2×=.
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
