【素养目标】2023-2024学年初中数学湘教版八年级下册1.2 第2课时 勾股定理的应用 学案 (含答案)
文档属性
| 名称 | 【素养目标】2023-2024学年初中数学湘教版八年级下册1.2 第2课时 勾股定理的应用 学案 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览

文档简介
1.2 第2课时 勾股定理的应用
素养目标
1.结合实际,利用勾股定理解决求直角三角形的边长问题.
2.在应用过程中掌握“转化”思想,在没有直角三角形的图形中,通过构造出直角三角形再利用勾股定理解决实际问题.
◎重点:应用勾股定理知识解决有关问题.
预习导学
知识点 勾股定理的应用
阅读课本本课时的全部内容,回答下列问题.
1.“动脑筋”中梯子的底部从点C移到点C',则梯子的顶部从点A移到点 .所以梯子底部移动的距离是线段CC'的长,而顶部移动的距离是线段 的长.
2.“动脑筋”的图中的直角三角形有两个,分别是 和 ,梯子的长是两个直角三角形的斜边 和 ,它们的长度 ,所以两个直角三角形的两直角边的平方和 .
3.“例2”解决的是已知一边B'C,并且能找出另外两边AB',AC之间的关系 ,这样,只要设 个未知数,根据 即可得出方程,并解决问题.
【答案】1.A' AA'
2.Rt△ABC Rt△A'BC' AC A'C' 相等 相等
3.AC=AB—BC=AB'—AC 一 勾股定理
归纳总结 在斜边长不变的两个直角三角形中,两直角边的平方和 .
【答案】相等
对点自测
(1)如图,一根垂直于地面的旗杆在离地面5 m处折断,旗杆顶部落在离旗杆底部12 m处,则旗杆折断之前的高度是 ( )
A.5 m B.12 m C.13 m D.18 m
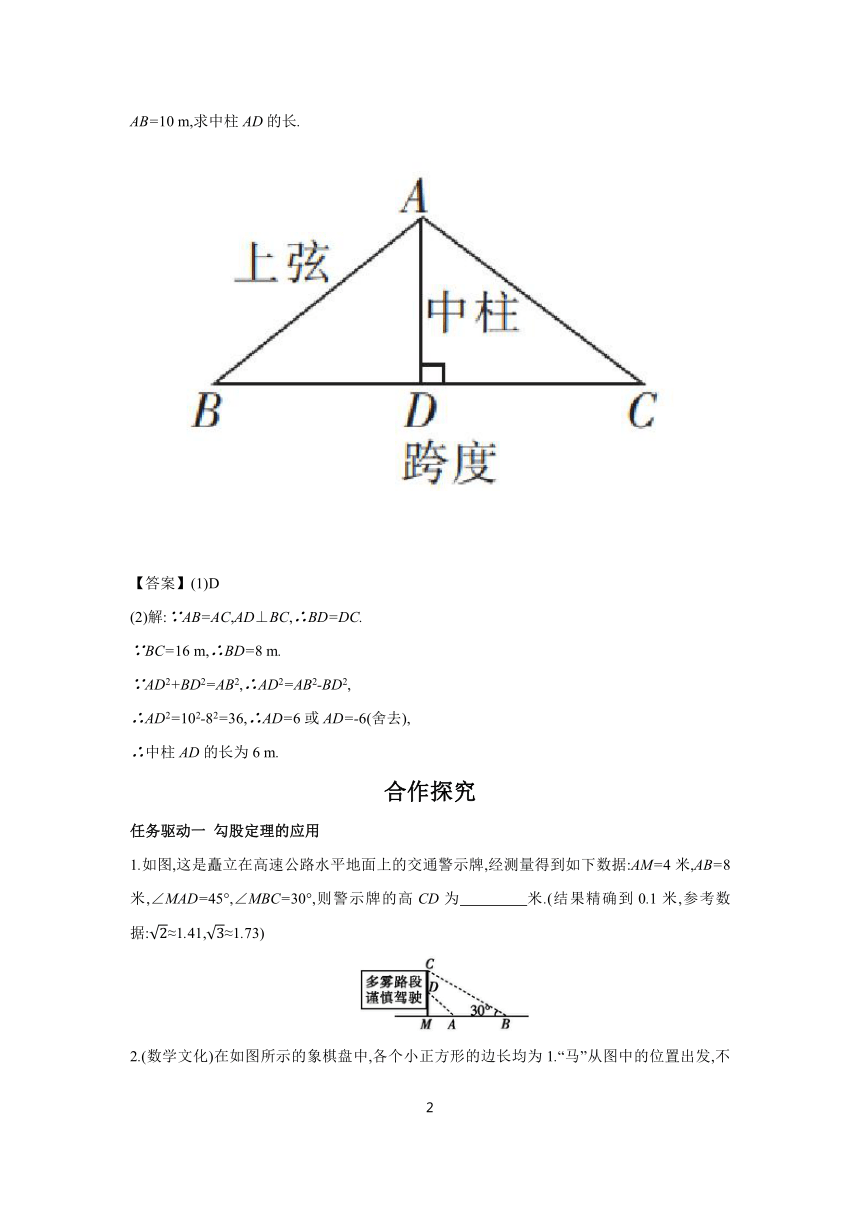
(2)如图,厂房屋顶的人字架是等腰三角形,AB=AC,AD⊥BC于点D,若跨度BC=16 m,上弦长AB=10 m,求中柱AD的长.
【答案】(1)D
(2)解:∵AB=AC,AD⊥BC,∴BD=DC.
∵BC=16 m,∴BD=8 m.
∵AD2+BD2=AB2,∴AD2=AB2-BD2,
∴AD2=102-82=36,∴AD=6或AD=-6(舍去),
∴中柱AD的长为6 m.
合作探究
任务驱动一 勾股定理的应用
1.如图,这是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
2.(数学文化)在如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
3.在甲村至乙村的公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险 是否需要暂时封锁 请通过计算进行说明.
【答案】1.2.9
2.
提示:如图,第一步到①,第二步到②,故走两步后的落点与出发点间的最短距离为=.
3.解:如图,过点C作CD⊥AB于点D.∵BC=400米,AC=300米,∠ACB=90°,∴根据勾股定理得AB=500米.∵AB·CD=BC·AC,∴CD=240米.∵240米<250米,故有危险,因此AB段公路需要暂时封锁.
方法归纳交流 本题的条件中含有60°,90°两个特殊角,但这两个特殊角都没有在直角三角形中,因此我们就用这两个特殊角构造一个或多个 三角形,以便用 定理去求相应边长.
【答案】直角 勾股
任务驱动二 方程思想在勾股定理中的应用
4.(数学文化)我国古代数学著作《九章算术》中记载了这样一个问题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何 ”大意:如图,木柱AB⊥BC,绳索AC比木柱AB长3尺,BC长8尺,则绳索AC的长为 尺.
5.如图,铁路上A,B两站相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10 km,现在要在铁路AB上建一个货运站E,使得C,D两村庄到E站的距离相等,则E站应建在离A站多少千米处
【答案】4.
提示:设AC=x尺,则AB=(x-3)尺.
∵AB⊥BC,∴∠ABC=90°,
∴△ABC是直角三角形.
由勾股定理得AB2+BC2=AC2,
即(x-3)2+82=x2,
解得x=,即绳索AC的长为尺.
故答案为.
5.解:∵C,D两村到E站的距离相等,∴DE=CE.
∵DA⊥AB于点A,CB⊥AB于点B,
∴∠A=∠B=90°,
∴AE2+DA2=DE2,BE2+CB2=CE2,
∴AE2+DA2=BE2+CB2,设AE=x km,则BE=AB-AE=(25-x) km.
∵DA=15 km,CB=10 km,
∴x2+152=(25-x)2+102,解得x=10,∴AE=10 km.
答:E站应建在离A站10 km处.
2
素养目标
1.结合实际,利用勾股定理解决求直角三角形的边长问题.
2.在应用过程中掌握“转化”思想,在没有直角三角形的图形中,通过构造出直角三角形再利用勾股定理解决实际问题.
◎重点:应用勾股定理知识解决有关问题.
预习导学
知识点 勾股定理的应用
阅读课本本课时的全部内容,回答下列问题.
1.“动脑筋”中梯子的底部从点C移到点C',则梯子的顶部从点A移到点 .所以梯子底部移动的距离是线段CC'的长,而顶部移动的距离是线段 的长.
2.“动脑筋”的图中的直角三角形有两个,分别是 和 ,梯子的长是两个直角三角形的斜边 和 ,它们的长度 ,所以两个直角三角形的两直角边的平方和 .
3.“例2”解决的是已知一边B'C,并且能找出另外两边AB',AC之间的关系 ,这样,只要设 个未知数,根据 即可得出方程,并解决问题.
【答案】1.A' AA'
2.Rt△ABC Rt△A'BC' AC A'C' 相等 相等
3.AC=AB—BC=AB'—AC 一 勾股定理
归纳总结 在斜边长不变的两个直角三角形中,两直角边的平方和 .
【答案】相等
对点自测
(1)如图,一根垂直于地面的旗杆在离地面5 m处折断,旗杆顶部落在离旗杆底部12 m处,则旗杆折断之前的高度是 ( )
A.5 m B.12 m C.13 m D.18 m
(2)如图,厂房屋顶的人字架是等腰三角形,AB=AC,AD⊥BC于点D,若跨度BC=16 m,上弦长AB=10 m,求中柱AD的长.
【答案】(1)D
(2)解:∵AB=AC,AD⊥BC,∴BD=DC.
∵BC=16 m,∴BD=8 m.
∵AD2+BD2=AB2,∴AD2=AB2-BD2,
∴AD2=102-82=36,∴AD=6或AD=-6(舍去),
∴中柱AD的长为6 m.
合作探究
任务驱动一 勾股定理的应用
1.如图,这是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
2.(数学文化)在如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
3.在甲村至乙村的公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上另一停靠站B的距离为400米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险 是否需要暂时封锁 请通过计算进行说明.
【答案】1.2.9
2.
提示:如图,第一步到①,第二步到②,故走两步后的落点与出发点间的最短距离为=.
3.解:如图,过点C作CD⊥AB于点D.∵BC=400米,AC=300米,∠ACB=90°,∴根据勾股定理得AB=500米.∵AB·CD=BC·AC,∴CD=240米.∵240米<250米,故有危险,因此AB段公路需要暂时封锁.
方法归纳交流 本题的条件中含有60°,90°两个特殊角,但这两个特殊角都没有在直角三角形中,因此我们就用这两个特殊角构造一个或多个 三角形,以便用 定理去求相应边长.
【答案】直角 勾股
任务驱动二 方程思想在勾股定理中的应用
4.(数学文化)我国古代数学著作《九章算术》中记载了这样一个问题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何 ”大意:如图,木柱AB⊥BC,绳索AC比木柱AB长3尺,BC长8尺,则绳索AC的长为 尺.
5.如图,铁路上A,B两站相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10 km,现在要在铁路AB上建一个货运站E,使得C,D两村庄到E站的距离相等,则E站应建在离A站多少千米处
【答案】4.
提示:设AC=x尺,则AB=(x-3)尺.
∵AB⊥BC,∴∠ABC=90°,
∴△ABC是直角三角形.
由勾股定理得AB2+BC2=AC2,
即(x-3)2+82=x2,
解得x=,即绳索AC的长为尺.
故答案为.
5.解:∵C,D两村到E站的距离相等,∴DE=CE.
∵DA⊥AB于点A,CB⊥AB于点B,
∴∠A=∠B=90°,
∴AE2+DA2=DE2,BE2+CB2=CE2,
∴AE2+DA2=BE2+CB2,设AE=x km,则BE=AB-AE=(25-x) km.
∵DA=15 km,CB=10 km,
∴x2+152=(25-x)2+102,解得x=10,∴AE=10 km.
答:E站应建在离A站10 km处.
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
