2.2.2 第2课时 运用对角线判定平行四边形 学案 2023-2024学年初中数学湘教版八年级下册(含答案)
文档属性
| 名称 | 2.2.2 第2课时 运用对角线判定平行四边形 学案 2023-2024学年初中数学湘教版八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 125.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 07:47:39 | ||
图片预览

文档简介
2.2.2 第2课时 运用对角线判定平行四边形
素养目标
1.掌握对角线互相平分的四边形是平行四边形.
2.理解两组对角分别相等的四边形是平行四边形.
3.综合已知条件,能选择适当的判定方法,判定平行四边形.
◎重点:平行四边形的判定.
预习导学
知识点一 对角线互相平分的四边形
阅读课本本课时“例8”之前的所有内容,回答下列问题.
1.猜想:观察“图2-26”,取任意长的两根木条,将两根木条的中点重合,并用一颗钉子固定好,你认为以两根木条的端点作为顶点的四边形是平行四边形吗
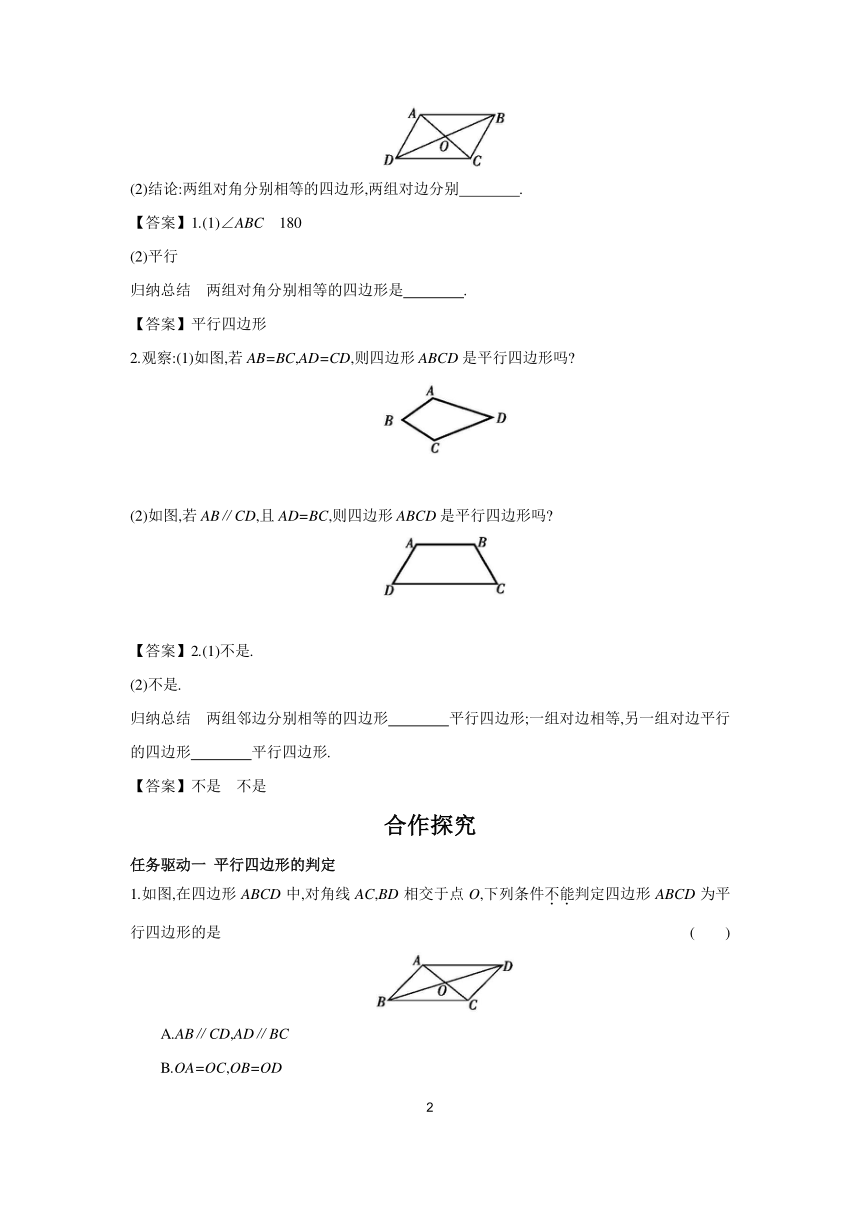
2.(1)验证:如图,若四边形ABCD对角线相互平分,即OA=OC,OB=OD,则△AOB≌△COD,理由是 ,则AB CD,∠BAO= ,所以AB∥ ,故四边形ABCD是平行四边形.
(2)结论:对角线相互平分的四边形是 .
3.应用:在“例7”中,说明四边形AECF是平行四边形的依据是什么
【答案】1.是的.
2.(1)SAS = ∠OCD CD
(2)平行四边形
3.对角线相互平分的四边形是平行四边形.
知识点二 对角相等的四边形
1.(1)推理:如图,若∠DAB=∠DCB,∠ADC=∠ABC,则∠DAB+∠ADC=∠DAB+ = °,则AB∥CD,AD∥BC.
(2)结论:两组对角分别相等的四边形,两组对边分别 .
【答案】1.(1)∠ABC 180
(2)平行
归纳总结 两组对角分别相等的四边形是 .
【答案】平行四边形
2.观察:(1)如图,若AB=BC,AD=CD,则四边形ABCD是平行四边形吗
(2)如图,若AB∥CD,且AD=BC,则四边形ABCD是平行四边形吗
【答案】2.(1)不是.
(2)不是.
归纳总结 两组邻边分别相等的四边形 平行四边形;一组对边相等,另一组对边平行的四边形 平行四边形.
【答案】不是 不是
合作探究
任务驱动一 平行四边形的判定
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是 ( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
方法归纳交流 上一课时与本课时,我们学完了全部平行四边形的判定定理,解决本题需要综合考虑所有情形.有一些条件无法直接使用,需要推理转化之后,才能成为判定平行四边形的前提条件.
2.如图1,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是 ( )
A.甲、乙、丙
B.只有甲、乙
C.只有甲、丙
D.只有乙、丙
【答案】1.C
2.A
任务驱动二 平行四边形的判定与性质综合
3.如图,E,F是 ABCD对角线AC上的两点,且AE=CF,连接BE,DE,BF,DF.
(1)求证:四边形BEDF是平行四边形.
(2)若AB⊥BF,AB=4,BF=3,AC=8.
①求线段EF的长;
②求四边形BEDF的面积.
4.如图,AE=EC,FG∥AB,AG∥BC.
(1)证明:△AGE≌△CFE.
(2)说明四边形ABFG是平行四边形.
(3)若过点E作ED∥BC交AB于点D,试判断DE与BC的数量关系,并说明理由.
【答案】3.解:(1)证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OA-AE=OC-CF,即OE=OF.
又∵OB=OD,
∴四边形BEDF是平行四边形.
(2)①∵AB⊥BF,
∴∠ABF=90°,
∴AF===5.
∵AC=8,
∴CF=AC-AF=8-5=3.
∵AE=CF=3,
∴EF=AF-AE=5-3=2.
②∵AB⊥BF,
∴∠ABF=90°,
∴S△ABF=AB·BF=×4×3=6.
由①可知,EF=2,AF=5,
∴S△BEF=S△ABF=×6=.
由(1)可知,四边形BEDF是平行四边形,
∴S平行四边形BEDF=2S△BEF=.
4.解:(1)证明:∵AG∥BC,
∴∠GAE=∠C,
∵∠AEG=∠CEF,AE=EC,
∴△AGE≌△CFE.
(2)∵AG∥BF,FG∥AB,
∴四边形ABFG是平行四边形.
(3)DE=BC.
理由:∵DE∥BC,BD∥EF,
∴四边形BDEF是平行四边形,
∴DE=BF.
由(1)可知,AG=FC,
由(2)可知,AG=BF,∴FC=BF,
∴DE=BF=FC,
∴DE=BC.
方法归纳交流 证明一个四边形是平行四边形之后,常常可以利用这个平行四边形的性质,再推理出其他的结论.
2
素养目标
1.掌握对角线互相平分的四边形是平行四边形.
2.理解两组对角分别相等的四边形是平行四边形.
3.综合已知条件,能选择适当的判定方法,判定平行四边形.
◎重点:平行四边形的判定.
预习导学
知识点一 对角线互相平分的四边形
阅读课本本课时“例8”之前的所有内容,回答下列问题.
1.猜想:观察“图2-26”,取任意长的两根木条,将两根木条的中点重合,并用一颗钉子固定好,你认为以两根木条的端点作为顶点的四边形是平行四边形吗
2.(1)验证:如图,若四边形ABCD对角线相互平分,即OA=OC,OB=OD,则△AOB≌△COD,理由是 ,则AB CD,∠BAO= ,所以AB∥ ,故四边形ABCD是平行四边形.
(2)结论:对角线相互平分的四边形是 .
3.应用:在“例7”中,说明四边形AECF是平行四边形的依据是什么
【答案】1.是的.
2.(1)SAS = ∠OCD CD
(2)平行四边形
3.对角线相互平分的四边形是平行四边形.
知识点二 对角相等的四边形
1.(1)推理:如图,若∠DAB=∠DCB,∠ADC=∠ABC,则∠DAB+∠ADC=∠DAB+ = °,则AB∥CD,AD∥BC.
(2)结论:两组对角分别相等的四边形,两组对边分别 .
【答案】1.(1)∠ABC 180
(2)平行
归纳总结 两组对角分别相等的四边形是 .
【答案】平行四边形
2.观察:(1)如图,若AB=BC,AD=CD,则四边形ABCD是平行四边形吗
(2)如图,若AB∥CD,且AD=BC,则四边形ABCD是平行四边形吗
【答案】2.(1)不是.
(2)不是.
归纳总结 两组邻边分别相等的四边形 平行四边形;一组对边相等,另一组对边平行的四边形 平行四边形.
【答案】不是 不是
合作探究
任务驱动一 平行四边形的判定
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是 ( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
方法归纳交流 上一课时与本课时,我们学完了全部平行四边形的判定定理,解决本题需要综合考虑所有情形.有一些条件无法直接使用,需要推理转化之后,才能成为判定平行四边形的前提条件.
2.如图1,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是 ( )
A.甲、乙、丙
B.只有甲、乙
C.只有甲、丙
D.只有乙、丙
【答案】1.C
2.A
任务驱动二 平行四边形的判定与性质综合
3.如图,E,F是 ABCD对角线AC上的两点,且AE=CF,连接BE,DE,BF,DF.
(1)求证:四边形BEDF是平行四边形.
(2)若AB⊥BF,AB=4,BF=3,AC=8.
①求线段EF的长;
②求四边形BEDF的面积.
4.如图,AE=EC,FG∥AB,AG∥BC.
(1)证明:△AGE≌△CFE.
(2)说明四边形ABFG是平行四边形.
(3)若过点E作ED∥BC交AB于点D,试判断DE与BC的数量关系,并说明理由.
【答案】3.解:(1)证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OA-AE=OC-CF,即OE=OF.
又∵OB=OD,
∴四边形BEDF是平行四边形.
(2)①∵AB⊥BF,
∴∠ABF=90°,
∴AF===5.
∵AC=8,
∴CF=AC-AF=8-5=3.
∵AE=CF=3,
∴EF=AF-AE=5-3=2.
②∵AB⊥BF,
∴∠ABF=90°,
∴S△ABF=AB·BF=×4×3=6.
由①可知,EF=2,AF=5,
∴S△BEF=S△ABF=×6=.
由(1)可知,四边形BEDF是平行四边形,
∴S平行四边形BEDF=2S△BEF=.
4.解:(1)证明:∵AG∥BC,
∴∠GAE=∠C,
∵∠AEG=∠CEF,AE=EC,
∴△AGE≌△CFE.
(2)∵AG∥BF,FG∥AB,
∴四边形ABFG是平行四边形.
(3)DE=BC.
理由:∵DE∥BC,BD∥EF,
∴四边形BDEF是平行四边形,
∴DE=BF.
由(1)可知,AG=FC,
由(2)可知,AG=BF,∴FC=BF,
∴DE=BF=FC,
∴DE=BC.
方法归纳交流 证明一个四边形是平行四边形之后,常常可以利用这个平行四边形的性质,再推理出其他的结论.
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
