[素养目标]2.5.1 矩形的性质学案(含答案) 2023-2024学年初中数学湘教版八年级下册
文档属性
| 名称 | [素养目标]2.5.1 矩形的性质学案(含答案) 2023-2024学年初中数学湘教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览

文档简介
2.5.1 矩形的性质
素养目标
1.明确矩形的定义,知道矩形是特殊的平行四边形.
2.会从边、角、角平分线、对称性四个方面掌握矩形的性质.
3.理解直角三角形的性质,并能解决相关几何问题.
◎重点:矩形的性质.
预习导学
知识点一 矩形的边、内角、对角线的性质
阅读课本本课时“例1”及其之前的所有内容,回答下列问题.
1.明晰概念:有一个角是 的 叫做矩形.
2.(1)思考:平行四边形一定是矩形吗 矩形一定是平行四边形吗
(2)结论:矩形 (填“具有”或“不具有”)平行四边形的所有性质.
3.思考:(1)如图,由平行四边形的对边平行,可知相邻的两个内角之和为 ,又因为矩形有一个内角是直角,则其他的三个内角也为 .
(2)如上图,△ABC与△BAD全等吗 能得到关于矩形的对角线什么性质
【答案】1.直角 平行四边形
2.(1)不一定;一定.
(2)具有
3.(1)180° 直角
(2)由AD=BC,AB=BA,∠DAB=∠ABC,可知△ABC≌△BAD,可知AC=BD.
归纳总结 矩形的两组对边与平行四边形一样,分别 ;矩形的四个内角都为 ;矩形的对角线互相平分且 .
【答案】平行且相等 直角 相等
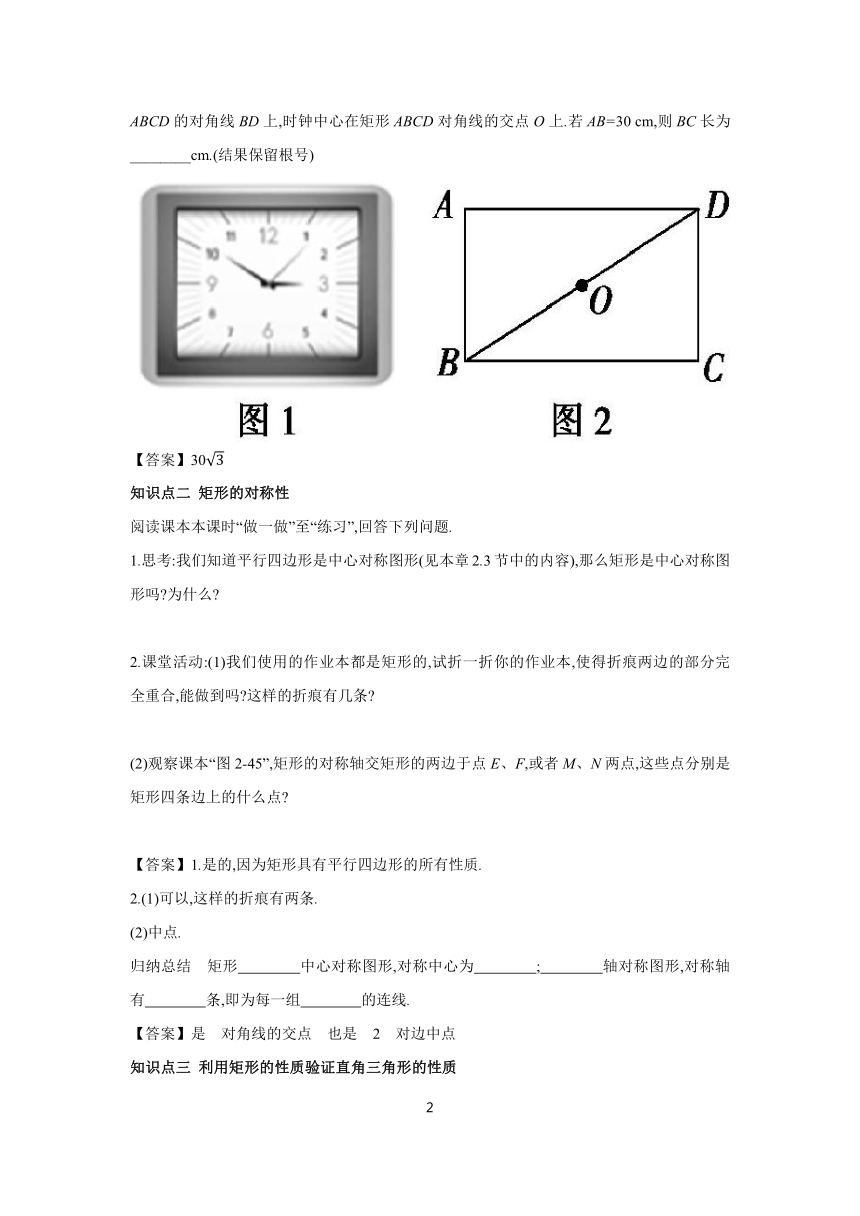
对点自测 如图1,这是一种矩形时钟,如图2,这是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB=30 cm,则BC长为________cm.(结果保留根号)
【答案】30
知识点二 矩形的对称性
阅读课本本课时“做一做”至“练习”,回答下列问题.
1.思考:我们知道平行四边形是中心对称图形(见本章2.3节中的内容),那么矩形是中心对称图形吗 为什么
2.课堂活动:(1)我们使用的作业本都是矩形的,试折一折你的作业本,使得折痕两边的部分完全重合,能做到吗 这样的折痕有几条
(2)观察课本“图2-45”,矩形的对称轴交矩形的两边于点E、F,或者M、N两点,这些点分别是矩形四条边上的什么点
【答案】1.是的,因为矩形具有平行四边形的所有性质.
2.(1)可以,这样的折痕有两条.
(2)中点.
归纳总结 矩形 中心对称图形,对称中心为 ; 轴对称图形,对称轴有 条,即为每一组 的连线.
【答案】是 对角线的交点 也是 2 对边中点
知识点三 利用矩形的性质验证直角三角形的性质
阅读课本本课时“练习2”的内容,回答下列问题.
1.如图,若四边形ABCD为矩形,则对角线AC与BD互相平分且相等.讨论:
(1)△ACD为 三角形,OD为△ACD 线.
(2)OC,OA,OD,OB有什么关系
2.揭示概念:直角三角形斜边上的中线等于 .
【答案】1.(1)直角 斜边上的中
(2)相等.
2.斜边的一半
合作探究
任务驱动一 矩形的性质
1.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是 ( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
2.如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【答案】1.D
2.证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°.
∵EF⊥DF,∴∠EFD=90°,
∴∠EFB+∠CFD=90°.
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD(ASA),
∴BF=CD.
任务驱动二 矩形的折叠问题
3.如图,在一张矩形纸片ABCD中,AD=4 cm,E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为 ( )
A.2 cm B.2 cm
C.4 cm D.4 cm
4.如果将长为6 cm,宽为5 cm的矩形纸片折叠一次,那么这条折痕的长不可能是 ( )
A.8 cm B.5cm
C.5.5 cm D.1 cm
【答案】3.B
4.A
任务驱动三 矩形中的分类讨论
5.在矩形ABCD中,AB=8,AD=7,点E在AB边上,AE=5.若P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .
【答案】5.5或4.
提示:如图,
当AP=AE=5时,∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=AE=5;
当P1E=AE=5时,∵BE=AB-AE=8-5=3,∠B=90°,
∴P1B==4,
∴底边AP1==4.
综上所述,等腰三角形AEP的底边长为5或4.
2
素养目标
1.明确矩形的定义,知道矩形是特殊的平行四边形.
2.会从边、角、角平分线、对称性四个方面掌握矩形的性质.
3.理解直角三角形的性质,并能解决相关几何问题.
◎重点:矩形的性质.
预习导学
知识点一 矩形的边、内角、对角线的性质
阅读课本本课时“例1”及其之前的所有内容,回答下列问题.
1.明晰概念:有一个角是 的 叫做矩形.
2.(1)思考:平行四边形一定是矩形吗 矩形一定是平行四边形吗
(2)结论:矩形 (填“具有”或“不具有”)平行四边形的所有性质.
3.思考:(1)如图,由平行四边形的对边平行,可知相邻的两个内角之和为 ,又因为矩形有一个内角是直角,则其他的三个内角也为 .
(2)如上图,△ABC与△BAD全等吗 能得到关于矩形的对角线什么性质
【答案】1.直角 平行四边形
2.(1)不一定;一定.
(2)具有
3.(1)180° 直角
(2)由AD=BC,AB=BA,∠DAB=∠ABC,可知△ABC≌△BAD,可知AC=BD.
归纳总结 矩形的两组对边与平行四边形一样,分别 ;矩形的四个内角都为 ;矩形的对角线互相平分且 .
【答案】平行且相等 直角 相等
对点自测 如图1,这是一种矩形时钟,如图2,这是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB=30 cm,则BC长为________cm.(结果保留根号)
【答案】30
知识点二 矩形的对称性
阅读课本本课时“做一做”至“练习”,回答下列问题.
1.思考:我们知道平行四边形是中心对称图形(见本章2.3节中的内容),那么矩形是中心对称图形吗 为什么
2.课堂活动:(1)我们使用的作业本都是矩形的,试折一折你的作业本,使得折痕两边的部分完全重合,能做到吗 这样的折痕有几条
(2)观察课本“图2-45”,矩形的对称轴交矩形的两边于点E、F,或者M、N两点,这些点分别是矩形四条边上的什么点
【答案】1.是的,因为矩形具有平行四边形的所有性质.
2.(1)可以,这样的折痕有两条.
(2)中点.
归纳总结 矩形 中心对称图形,对称中心为 ; 轴对称图形,对称轴有 条,即为每一组 的连线.
【答案】是 对角线的交点 也是 2 对边中点
知识点三 利用矩形的性质验证直角三角形的性质
阅读课本本课时“练习2”的内容,回答下列问题.
1.如图,若四边形ABCD为矩形,则对角线AC与BD互相平分且相等.讨论:
(1)△ACD为 三角形,OD为△ACD 线.
(2)OC,OA,OD,OB有什么关系
2.揭示概念:直角三角形斜边上的中线等于 .
【答案】1.(1)直角 斜边上的中
(2)相等.
2.斜边的一半
合作探究
任务驱动一 矩形的性质
1.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是 ( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
2.如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
【答案】1.D
2.证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°.
∵EF⊥DF,∴∠EFD=90°,
∴∠EFB+∠CFD=90°.
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD(ASA),
∴BF=CD.
任务驱动二 矩形的折叠问题
3.如图,在一张矩形纸片ABCD中,AD=4 cm,E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为 ( )
A.2 cm B.2 cm
C.4 cm D.4 cm
4.如果将长为6 cm,宽为5 cm的矩形纸片折叠一次,那么这条折痕的长不可能是 ( )
A.8 cm B.5cm
C.5.5 cm D.1 cm
【答案】3.B
4.A
任务驱动三 矩形中的分类讨论
5.在矩形ABCD中,AB=8,AD=7,点E在AB边上,AE=5.若P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .
【答案】5.5或4.
提示:如图,
当AP=AE=5时,∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=AE=5;
当P1E=AE=5时,∵BE=AB-AE=8-5=3,∠B=90°,
∴P1B==4,
∴底边AP1==4.
综上所述,等腰三角形AEP的底边长为5或4.
2
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
