9.1.2 三角形的内角和与外角和 第1课时 学案(含答案) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 第1课时 学案(含答案) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:13:28 | ||
图片预览


文档简介
9.1.2 三角形的内角和与外角和 第1课时
素养目标
1.经历探索证明三角形内角和定理的过程,能利用平行线的性质推出这一定理.
2.能推出直角三角形的两内角互余.
3.能应用三角形的内角和定理解决一些简单问题.
◎重点:证明三角形的内角和定理,推出直角三角形的两内角互余.
预习导学
知识点一 三角形内角和定理
请你阅读课本本节开始至“等量代换”的内容,思考:三角形的内角和是多少度 如何证明这一结论
温馨提示:准备若干三角形的纸片.
动手操作:小学我们学过用剪和拼的方法求三角形的内角和,你有哪些拼图的方法可以求出三角形的内角和 动手拼一拼,试一试.
证明定理:根据你所拼出的图形,画出图形证明三角形内角和定理.
得出结论:三角形的内角和是 .
【答案】解:答案不唯一,如下.
证明定理 答案不唯一,学生只要选出一种拼图方法证明即可.如下.
证明:如图,以点C为顶点,CA为一边作∠ACM=∠A,
由此可以得出:AB∥CM(内错角相等,两直线平行),
∴∠B+∠BCM=180°,
∴∠B+∠3+∠2=180°,即∠A+∠B+∠BCA=180°.
得出结论 180°
对点自测 在△ABC中,若∠A=80°,∠C=20°,则∠B= ;若∠A=80°,∠B=∠C,则∠C= .
【答案】80° 50°
知识点二 三角形内角和定理的推论
证明定理:在△ABC中,若∠A=90°,则∠B与∠C有什么关系 证明你的结论.
得出结论:直角三角形的两个锐角 .
【答案】证明定理 解:∠B与∠C互余.
证明:∵∠A+∠B+∠C=180°,∠A=90°,∴∠B+∠C=180°-∠A=180°-90°=90°.
得出结论 互余
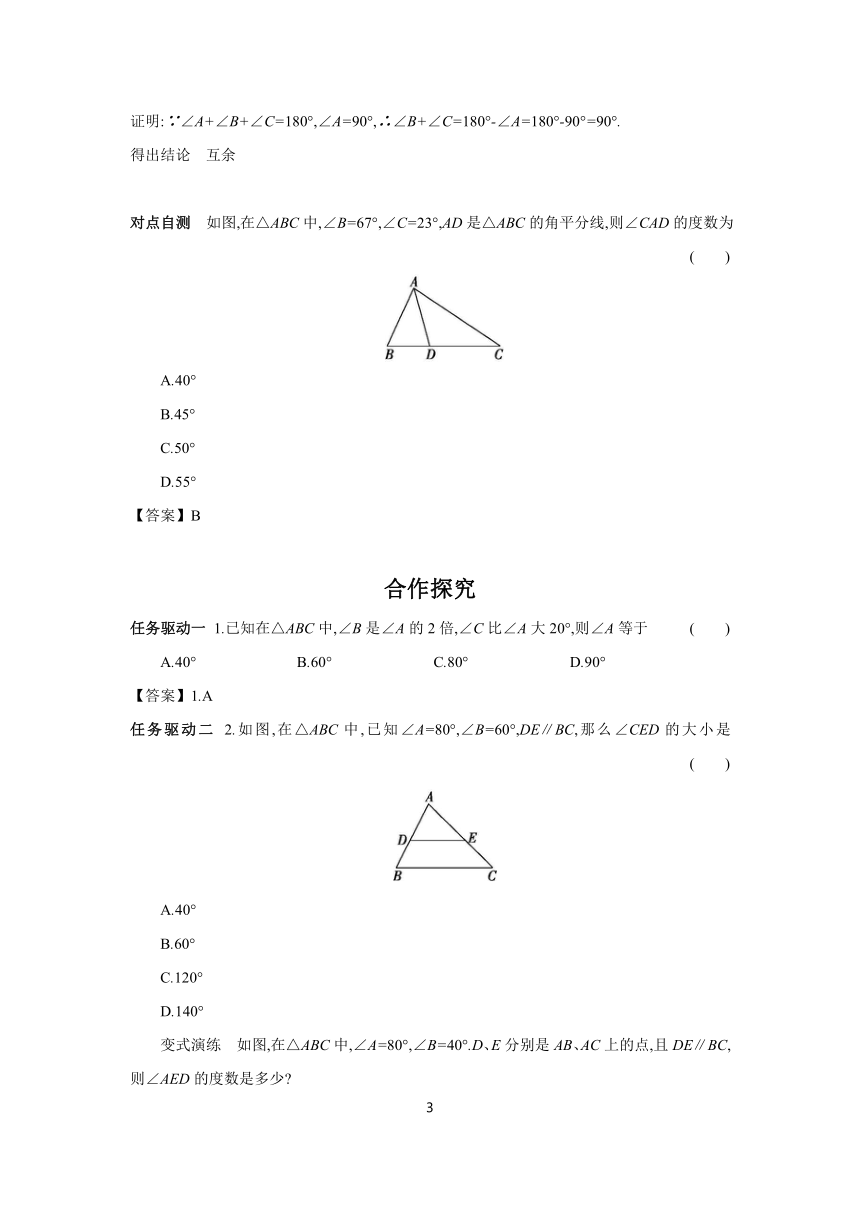
对点自测 如图,在△ABC中,∠B=67°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为 ( )
A.40°
B.45°
C.50°
D.55°
【答案】B
合作探究
任务驱动一 1.已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于 ( )
A.40° B.60° C.80° D.90°
【答案】1.A
任务驱动二 2.如图,在△ABC中,已知∠A=80°,∠B=60°,DE∥BC,那么∠CED的大小是 ( )
A.40°
B.60°
C.120°
D.140°
变式演练 如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB、AC上的点,且DE∥BC,则∠AED的度数是多少
方法归纳交流 解题时,要挖掘出隐含在题干中的已知条件:三角形的内角和是 .
【答案】2.D
变式演练
解:∵DE∥BC(已知),∠B=40°(已知),
∴∠ADE=∠B=40°(两直线平行,同位角相等).
又∵∠A=80°,
∴在△ADE中,∠AED=180°-∠A-∠ADE=60°(三角形内角和定理).
方法归纳交流 180°
任务驱动三 3.将一副直角三角板按如图所示的方式放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 ( )
A.45° B.60° C.75° D.85°
【答案】3.A
任务驱动四 4.如图,BO、CO分别平分∠ABC和∠ACB.
(1)若∠A=60°,求∠O的度数.
(2)若∠ABC+∠ACB=116°,则∠BOC= .
(3)若∠A=100°,120°,∠O又是多少度
方法归纳交流 通过上面的计算,你知道∠A与∠BOC有什么大小关系吗 你能尝试加以说明吗
【答案】4.解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠1=∠2,∠3=∠4.
(1)∵∠A=60°,
∴∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,∴∠O=120°.
(2)122°
(3)若∠A=100°,∠O=140°;
若∠A=120°,∠O=150°.
方法归纳交流
解:∠BOC=90°+∠A.
根据角平分线的定义得∠OBC+∠OCB=(∠ABC+∠ACB),
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A.
2
素养目标
1.经历探索证明三角形内角和定理的过程,能利用平行线的性质推出这一定理.
2.能推出直角三角形的两内角互余.
3.能应用三角形的内角和定理解决一些简单问题.
◎重点:证明三角形的内角和定理,推出直角三角形的两内角互余.
预习导学
知识点一 三角形内角和定理
请你阅读课本本节开始至“等量代换”的内容,思考:三角形的内角和是多少度 如何证明这一结论
温馨提示:准备若干三角形的纸片.
动手操作:小学我们学过用剪和拼的方法求三角形的内角和,你有哪些拼图的方法可以求出三角形的内角和 动手拼一拼,试一试.
证明定理:根据你所拼出的图形,画出图形证明三角形内角和定理.
得出结论:三角形的内角和是 .
【答案】解:答案不唯一,如下.
证明定理 答案不唯一,学生只要选出一种拼图方法证明即可.如下.
证明:如图,以点C为顶点,CA为一边作∠ACM=∠A,
由此可以得出:AB∥CM(内错角相等,两直线平行),
∴∠B+∠BCM=180°,
∴∠B+∠3+∠2=180°,即∠A+∠B+∠BCA=180°.
得出结论 180°
对点自测 在△ABC中,若∠A=80°,∠C=20°,则∠B= ;若∠A=80°,∠B=∠C,则∠C= .
【答案】80° 50°
知识点二 三角形内角和定理的推论
证明定理:在△ABC中,若∠A=90°,则∠B与∠C有什么关系 证明你的结论.
得出结论:直角三角形的两个锐角 .
【答案】证明定理 解:∠B与∠C互余.
证明:∵∠A+∠B+∠C=180°,∠A=90°,∴∠B+∠C=180°-∠A=180°-90°=90°.
得出结论 互余
对点自测 如图,在△ABC中,∠B=67°,∠C=23°,AD是△ABC的角平分线,则∠CAD的度数为 ( )
A.40°
B.45°
C.50°
D.55°
【答案】B
合作探究
任务驱动一 1.已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于 ( )
A.40° B.60° C.80° D.90°
【答案】1.A
任务驱动二 2.如图,在△ABC中,已知∠A=80°,∠B=60°,DE∥BC,那么∠CED的大小是 ( )
A.40°
B.60°
C.120°
D.140°
变式演练 如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB、AC上的点,且DE∥BC,则∠AED的度数是多少
方法归纳交流 解题时,要挖掘出隐含在题干中的已知条件:三角形的内角和是 .
【答案】2.D
变式演练
解:∵DE∥BC(已知),∠B=40°(已知),
∴∠ADE=∠B=40°(两直线平行,同位角相等).
又∵∠A=80°,
∴在△ADE中,∠AED=180°-∠A-∠ADE=60°(三角形内角和定理).
方法归纳交流 180°
任务驱动三 3.将一副直角三角板按如图所示的方式放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 ( )
A.45° B.60° C.75° D.85°
【答案】3.A
任务驱动四 4.如图,BO、CO分别平分∠ABC和∠ACB.
(1)若∠A=60°,求∠O的度数.
(2)若∠ABC+∠ACB=116°,则∠BOC= .
(3)若∠A=100°,120°,∠O又是多少度
方法归纳交流 通过上面的计算,你知道∠A与∠BOC有什么大小关系吗 你能尝试加以说明吗
【答案】4.解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠1=∠2,∠3=∠4.
(1)∵∠A=60°,
∴∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,∴∠O=120°.
(2)122°
(3)若∠A=100°,∠O=140°;
若∠A=120°,∠O=150°.
方法归纳交流
解:∠BOC=90°+∠A.
根据角平分线的定义得∠OBC+∠OCB=(∠ABC+∠ACB),
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A.
2
