2023-2024学年初中数学华东师大版七年级下册第7章 一次方程组 复习课 学案(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版七年级下册第7章 一次方程组 复习课 学案(含答案) | 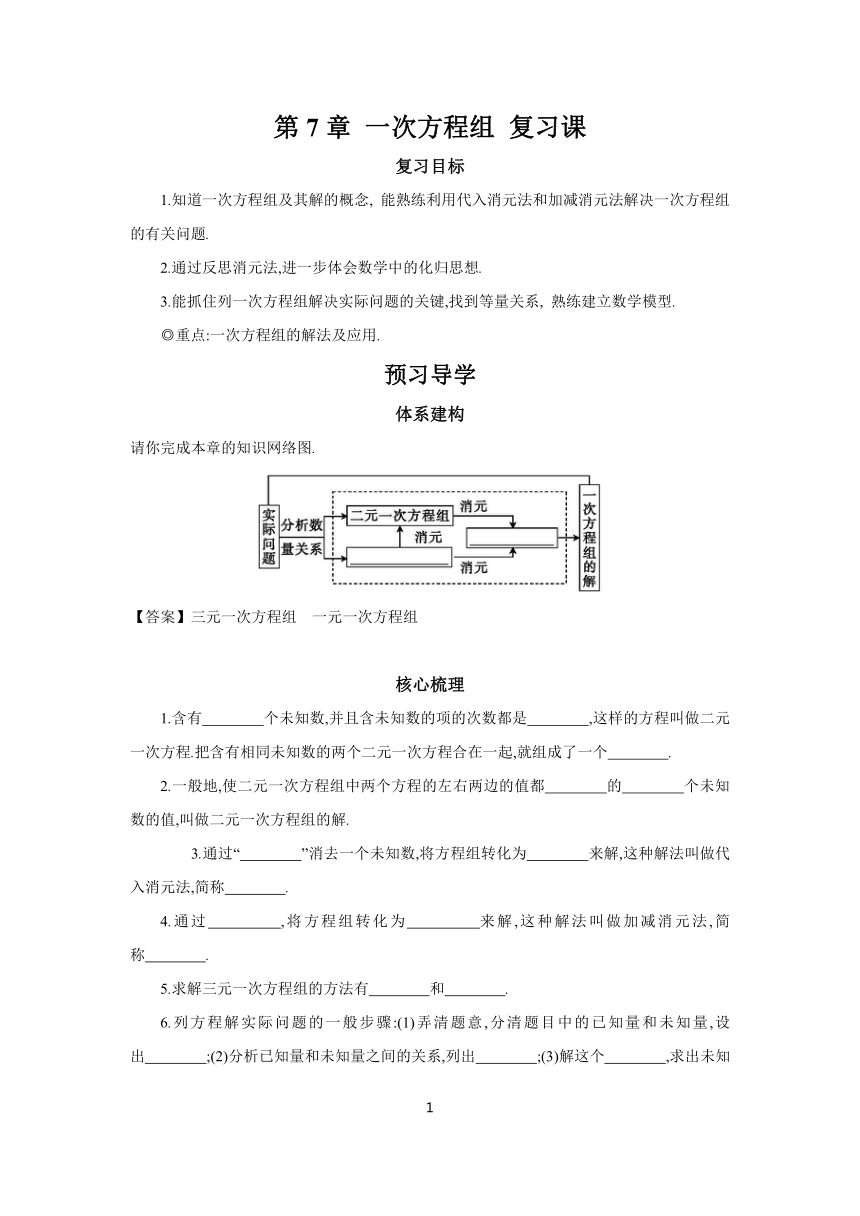 | |
| 格式 | docx | ||
| 文件大小 | 56.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:20:05 | ||
图片预览


文档简介
第7章 一次方程组 复习课
复习目标
1.知道一次方程组及其解的概念, 能熟练利用代入消元法和加减消元法解决一次方程组的有关问题.
2.通过反思消元法,进一步体会数学中的化归思想.
3.能抓住列一次方程组解决实际问题的关键,找到等量关系, 熟练建立数学模型.
◎重点:一次方程组的解法及应用.
预习导学
体系建构
请你完成本章的知识网络图.
【答案】三元一次方程组 一元一次方程组
核心梳理
1.含有 个未知数,并且含未知数的项的次数都是 ,这样的方程叫做二元一次方程.把含有相同未知数的两个二元一次方程合在一起,就组成了一个 .
2.一般地,使二元一次方程组中两个方程的左右两边的值都 的 个未知数的值,叫做二元一次方程组的解.
3.通过“ ”消去一个未知数,将方程组转化为 来解,这种解法叫做代入消元法,简称 .
4.通过 ,将方程组转化为 来解,这种解法叫做加减消元法,简称 .
5.求解三元一次方程组的方法有 和 .
6.列方程解实际问题的一般步骤:(1)弄清题意,分清题目中的已知量和未知量,设出 ;(2)分析已知量和未知量之间的关系,列出 ;(3)解这个 ,求出未知数的值;(4)检验结果是否符合题意,写出 .
【答案】1.两 1 二元一次方程组
2.相等 两
3.代入 一元一次方程 代入法
4.将两个方程的两边分别相加(或相减)消去一个未知数 一元一次方程 加减法
5.代入消元法 加减消元法
6.(1)未知数
(2)方程组
(3)方程组
(4)答案
合作探究
专题一 二元一次方程组及其解的概念
1.下列方程组是二元一次方程组的是( )
A. B.
C. D.
2.已知是关于x、y的方程组的解,则a-b的值为( )
A.1 B.2 C.3.5 D.4
3.若2xm+2n+1=3ym-n-2-1是关于x、y的二元一次方程,则m= ,n= .
方法归纳交流 二元一次方程必须满足三个条件:①含有两个未知数;②含未知数的项的最高次数为1;③ 方程.
【答案】1.D 2.C 3.2 -1
方法归纳交流 整式
专题二 二元一次方程组的解法
4.解二元一次方程组:
(1)(2)
(3)==1.
方法归纳交流 二元一次方程组的解法有 和 两种,解题时根据方程组的特点灵活选用不同解法.
【答案】4.解:(1)将①代入②,得2x-3(3x-5)=1,解得x=2.
把x=2代入①得y=1,所以
(2)①-②×2得x=-1,把x=-1代入②得y=2,所以
(3)原方程组可化为
②×2-①得5y=7,y=1.4,把y=1.4代入②,得x=0.8,所以
方法归纳交流 代入消元法 加减消元法
专题三 利用一次方程组解决实际问题
5.随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式.黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,如果黄先生乘汽车到福州,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克
6.某汽车运输公司计划装运甲、乙两种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只能装一种蔬菜),下表所示为装运甲、乙两种蔬菜的重量及利润.
甲 乙
每辆汽车能满装的吨数 1 1.5
每吨蔬菜可获利润/百元 7 4
若用8辆汽车装运甲、乙两种蔬菜共11吨到A地销售,问装运甲、乙两种蔬菜的汽车应各安排多少辆 此时共可获利多少元
方法归纳交流 找 是列方程组解应用题的关键.
【答案】5.解:设飞机和汽车每小时二氧化碳的排放量分别为x千克和y千克,
依题意得解得
所以3x-9y=54.
答:他此行将减少二氧化碳排放量54千克.
6.解:设装甲种蔬菜需安排汽车x辆,装乙种蔬菜需安排y辆,根据题意,
得解得
则共可获利1×2×700+1.5×6×400=5000(元).
答:略.
方法归纳交流 等量关系
专题四 整体代入法解方程组
7.解方程组:
方法归纳交流 把 看做一个整体后,解方程组的过程简化了.一般情况下,当两个方程中含有相同的代数式时,可以把这个相同的部分看做一个整体.
变式演练 解方程组:
【答案】7.解:将①代入②,得2x-3=1,解得x=2.把x=2代入①,得y=-1.所以
方法归纳交流 x-y
变式演练
解:由①得x+y=③, 将③代入②,得x=4.把x=4代入③,得y=-.所以
专题五 三元一次方程组的解法
8.解方程组
方法归纳交流 解三元一次方程组时,通常先把三元一次方程组转化为二元一次方程组,再把二元一次方程组转化为 来解.
【答案】8.解:①+②得5x-z=14,①+③得4x+3z=15,组成方程组得解得x=3,z=1,把x=3,z=1代入③得y=8,所以原方程组的解是
方法归纳交流 一元一次方程
2
复习目标
1.知道一次方程组及其解的概念, 能熟练利用代入消元法和加减消元法解决一次方程组的有关问题.
2.通过反思消元法,进一步体会数学中的化归思想.
3.能抓住列一次方程组解决实际问题的关键,找到等量关系, 熟练建立数学模型.
◎重点:一次方程组的解法及应用.
预习导学
体系建构
请你完成本章的知识网络图.
【答案】三元一次方程组 一元一次方程组
核心梳理
1.含有 个未知数,并且含未知数的项的次数都是 ,这样的方程叫做二元一次方程.把含有相同未知数的两个二元一次方程合在一起,就组成了一个 .
2.一般地,使二元一次方程组中两个方程的左右两边的值都 的 个未知数的值,叫做二元一次方程组的解.
3.通过“ ”消去一个未知数,将方程组转化为 来解,这种解法叫做代入消元法,简称 .
4.通过 ,将方程组转化为 来解,这种解法叫做加减消元法,简称 .
5.求解三元一次方程组的方法有 和 .
6.列方程解实际问题的一般步骤:(1)弄清题意,分清题目中的已知量和未知量,设出 ;(2)分析已知量和未知量之间的关系,列出 ;(3)解这个 ,求出未知数的值;(4)检验结果是否符合题意,写出 .
【答案】1.两 1 二元一次方程组
2.相等 两
3.代入 一元一次方程 代入法
4.将两个方程的两边分别相加(或相减)消去一个未知数 一元一次方程 加减法
5.代入消元法 加减消元法
6.(1)未知数
(2)方程组
(3)方程组
(4)答案
合作探究
专题一 二元一次方程组及其解的概念
1.下列方程组是二元一次方程组的是( )
A. B.
C. D.
2.已知是关于x、y的方程组的解,则a-b的值为( )
A.1 B.2 C.3.5 D.4
3.若2xm+2n+1=3ym-n-2-1是关于x、y的二元一次方程,则m= ,n= .
方法归纳交流 二元一次方程必须满足三个条件:①含有两个未知数;②含未知数的项的最高次数为1;③ 方程.
【答案】1.D 2.C 3.2 -1
方法归纳交流 整式
专题二 二元一次方程组的解法
4.解二元一次方程组:
(1)(2)
(3)==1.
方法归纳交流 二元一次方程组的解法有 和 两种,解题时根据方程组的特点灵活选用不同解法.
【答案】4.解:(1)将①代入②,得2x-3(3x-5)=1,解得x=2.
把x=2代入①得y=1,所以
(2)①-②×2得x=-1,把x=-1代入②得y=2,所以
(3)原方程组可化为
②×2-①得5y=7,y=1.4,把y=1.4代入②,得x=0.8,所以
方法归纳交流 代入消元法 加减消元法
专题三 利用一次方程组解决实际问题
5.随着人们环保意识的增强,“低碳生活”成为人们提倡的生活方式.黄先生要从某地到福州,若乘飞机需要3小时,乘汽车需要9小时.这两种交通工具每小时排放的二氧化碳总量为70千克,已知飞机每小时二氧化碳的排放量比汽车多44千克,如果黄先生乘汽车到福州,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克
6.某汽车运输公司计划装运甲、乙两种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只能装一种蔬菜),下表所示为装运甲、乙两种蔬菜的重量及利润.
甲 乙
每辆汽车能满装的吨数 1 1.5
每吨蔬菜可获利润/百元 7 4
若用8辆汽车装运甲、乙两种蔬菜共11吨到A地销售,问装运甲、乙两种蔬菜的汽车应各安排多少辆 此时共可获利多少元
方法归纳交流 找 是列方程组解应用题的关键.
【答案】5.解:设飞机和汽车每小时二氧化碳的排放量分别为x千克和y千克,
依题意得解得
所以3x-9y=54.
答:他此行将减少二氧化碳排放量54千克.
6.解:设装甲种蔬菜需安排汽车x辆,装乙种蔬菜需安排y辆,根据题意,
得解得
则共可获利1×2×700+1.5×6×400=5000(元).
答:略.
方法归纳交流 等量关系
专题四 整体代入法解方程组
7.解方程组:
方法归纳交流 把 看做一个整体后,解方程组的过程简化了.一般情况下,当两个方程中含有相同的代数式时,可以把这个相同的部分看做一个整体.
变式演练 解方程组:
【答案】7.解:将①代入②,得2x-3=1,解得x=2.把x=2代入①,得y=-1.所以
方法归纳交流 x-y
变式演练
解:由①得x+y=③, 将③代入②,得x=4.把x=4代入③,得y=-.所以
专题五 三元一次方程组的解法
8.解方程组
方法归纳交流 解三元一次方程组时,通常先把三元一次方程组转化为二元一次方程组,再把二元一次方程组转化为 来解.
【答案】8.解:①+②得5x-z=14,①+③得4x+3z=15,组成方程组得解得x=3,z=1,把x=3,z=1代入③得y=8,所以原方程组的解是
方法归纳交流 一元一次方程
2
