17.2.1 平面直角坐标系 学案(含答案)2023-2024学年初中数学华东师大版八年级下册
文档属性
| 名称 | 17.2.1 平面直角坐标系 学案(含答案)2023-2024学年初中数学华东师大版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 86.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览


文档简介
17.2.1 平面直角坐标系
素养目标
1.知道什么是平面直角坐标系以及横轴、纵轴、原点、坐标等有关概念.
2.能正确画出直角坐标系,以及根据点的坐标找出它的位置,并由点的位置确定它的坐标.
3.通过自己动手画图达到熟练的程度,并充分感受直角坐标系上的点和有序实数对是一一对应的含义.
◎重点:根据点的坐标找出它的位置,并由点的位置确定它的坐标.
预习导学
知识点一 平面直角坐标系
阅读本课时教材“回忆”,回答下列问题.
1.在电影票上,“12排13号”与“13排12号”中的“12”的含义 .(填“相同”或“不同”)
2.在教室里,怎样找一个同学的座位
3.电影院里的座位要由 个数确定下来.
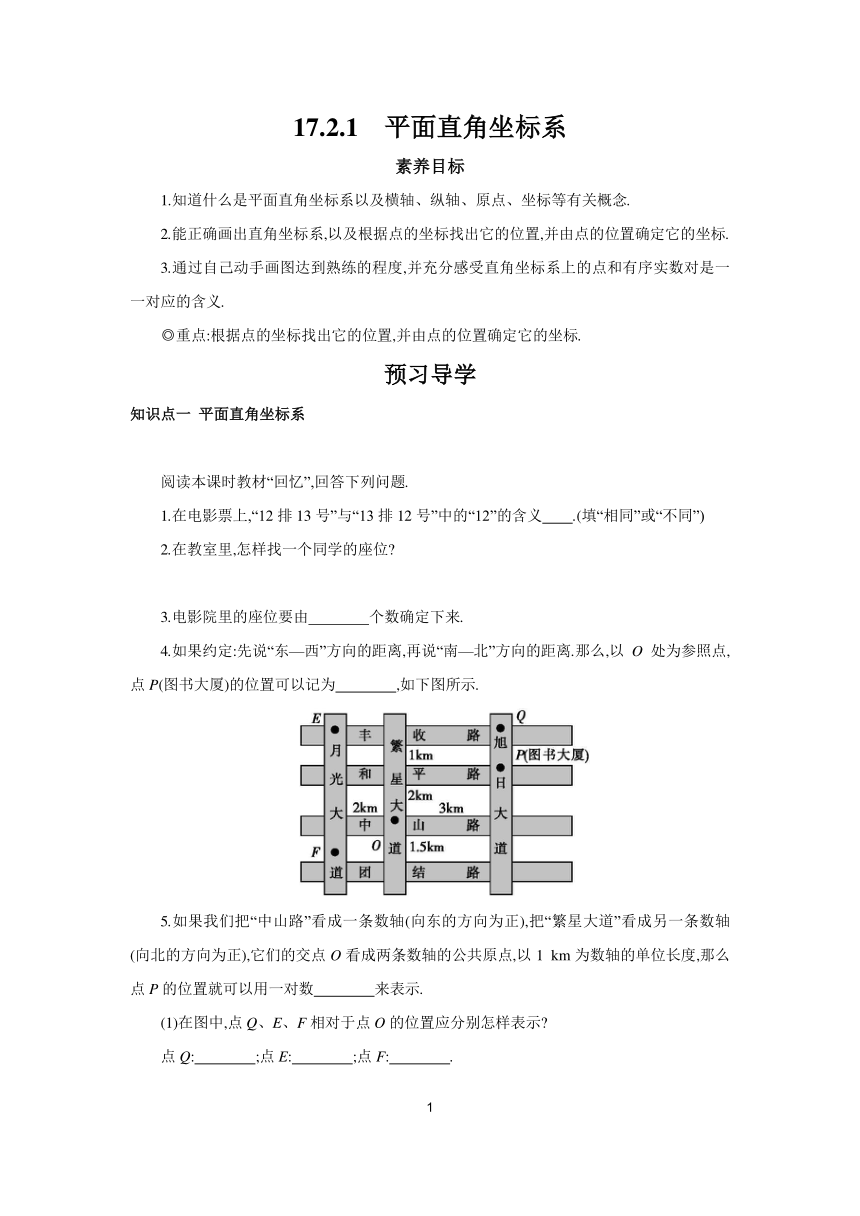
4.如果约定:先说“东—西”方向的距离,再说“南—北”方向的距离.那么,以O处为参照点,点P(图书大厦)的位置可以记为 ,如下图所示.
5.如果我们把“中山路”看成一条数轴(向东的方向为正),把“繁星大道”看成另一条数轴(向北的方向为正),它们的交点O看成两条数轴的公共原点,以1 km为数轴的单位长度,那么点P的位置就可以用一对数 来表示.
(1)在图中,点Q、E、F相对于点O的位置应分别怎样表示
点Q: ;点E: ;点F: .
(2)(3,-1.5)表示 位置;(-2,2)表示 位置.
(3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗 举例说明.
归纳总结 在平面上画两条 重合、互相 且具有 单位长度的数轴(教材“图17.2.2”),这就建立了平面 .通常把其中水平的一条数轴叫做x轴或 轴,取向 为正方向;铅直的数轴叫做y轴或 轴,取向 为正方向;两数轴的交点O叫做坐标 .
【答案】1.不同
2.首先找到第几排,再找这一排中的第几个座位.
3.两
4.(东3 km,北2 km)
5.(3,2)
(1)(东3 km,北3 km),即Q(3,3) (西2 km,北3 km),即E(-2,3) (西2 km,南1.5 km),即F(-2,-1.5)
(2)旭日大道与团结路交叉口 月光大道与和平路交叉口
(3)把中山路和繁星大道看成数轴后,就相当于把街道图无限延伸了,街道上任何一点都可以用一对数来表示.例如:月光大道和中山路交叉口可以表示为(-2,0).
归纳总结 原点 垂直 相同 直角坐标系 横 右 纵 上 原点
知识点二 点的坐标与象限
阅读本课时教材“回忆”下面至“练习”以上的部分,完成下列填空.
1.建立了平面直角坐标系后,两条坐标轴把平面分成4个区域,分别称为第一、二、三、四象限,坐标轴 (填“是”或“不”)属于任何一个象限.
2.第一象限( , ),第二象限( , ),第三象限( , ),第四象限( , )(填出“+”“-”号).
3.两条坐标轴上的点的坐标特点是:x轴上的点的纵坐标等于 ,反过来,纵坐标等于 的点都在x轴上;y轴上的点的横坐标等于 ,反过来,横坐标等于 的点都在y轴上.
4.若点在第一、三象限的角平分线上,它的 等于 ;若点在第二、四象限的角平分线上,它的横坐标与纵坐标 .
5.若两个点关于x轴对称,则 坐标相等, 坐标互为相反数;若两个点关于y轴对称,则 坐标相等, 坐标互为相反数;若两个点关于原点对称,则横坐标、纵坐标 .
归纳总结 1.在平面直角坐标系中,任意一点都可以用 来表示. 坐标在前, 坐标在后.
2.我们在坐标平面上可以看到:对于平面上的任意一点,都有唯一 (即这个点的坐标)与它对应;反过来,对任意一对有序实数,平面上都有唯一的 与它对应.这就是说,在平面直角坐标系中的 和 也是一一对应的.
【答案】1.不
2.+ + - + - - + -
3.0 0 0 0
4.纵坐标 横坐标 互为相反数
5.横 纵 纵 横 都互为相反数
归纳总结
1.一对有序实数 横 纵
2.一对有序实数 点 点 有序实数对
对点自测 已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P的坐标是 ( )
A.(-3,4) B.(3,4)
C.(-4,3) D.(4,3)
【答案】B
合作探究
任务驱动一 如图,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 .
【答案】(1,2)
任务驱动二 已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且M'到y轴的距离等于4,那么点M'的坐标是 ( )
A.(4,2)或(-4,2)
B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2)
D.(4,-2)或(-1,-2)
变式演练 如图,如果“”所在位置的坐标为(-1,-2),“”所在位置的坐标为(-3,1),那么,“”所在位置的坐标为 .
【答案】B
变式演练 (2,-2)
任务驱动三 (1)点A(2,-3)在第 象限.
(2)若点C(a-1,-b+3)在x轴上,则b= ;若点D(-3a-1,-2b+3)在y轴上,则a= .
(3)点P(5,-3)关于x轴对称的点的坐标是 ;点P(3,-5)关于y轴对称的点的坐标是 ;点P(-2,-4)关于原点对称的点的坐标是 .
【答案】(1)四
(2)3 -
(3)(5,3) (-3,-5) (2,4)
任务驱动四 (1)已知点A与点B(-1,6)关于x轴对称,求点A关于原点对称的点C的坐标.(2)到x轴的距离为2,到y轴的距离为3的点有几个 写出它们的坐标.
方法归纳交流 1.点(a,b)关于x轴、y轴、原点的对称点的坐标分别是 .
2.在坐标系中,点P(a,b)到x轴的距离为 ,到y轴的距离为 .
【答案】解:(1)因为点A与点B(-1,6)关于x轴对称,所以点A(-1,-6),点C(1,6).
(2)在每个象限内都有一个满足条件的点,故有4个点,它们的坐标分别是(3,2)、(-3,2)、(-3,-2)、(3,-2).
方法归纳交流
1.(a,-b)、(-a,b)、(-a,-b)
2.|b| |a|
2
素养目标
1.知道什么是平面直角坐标系以及横轴、纵轴、原点、坐标等有关概念.
2.能正确画出直角坐标系,以及根据点的坐标找出它的位置,并由点的位置确定它的坐标.
3.通过自己动手画图达到熟练的程度,并充分感受直角坐标系上的点和有序实数对是一一对应的含义.
◎重点:根据点的坐标找出它的位置,并由点的位置确定它的坐标.
预习导学
知识点一 平面直角坐标系
阅读本课时教材“回忆”,回答下列问题.
1.在电影票上,“12排13号”与“13排12号”中的“12”的含义 .(填“相同”或“不同”)
2.在教室里,怎样找一个同学的座位
3.电影院里的座位要由 个数确定下来.
4.如果约定:先说“东—西”方向的距离,再说“南—北”方向的距离.那么,以O处为参照点,点P(图书大厦)的位置可以记为 ,如下图所示.
5.如果我们把“中山路”看成一条数轴(向东的方向为正),把“繁星大道”看成另一条数轴(向北的方向为正),它们的交点O看成两条数轴的公共原点,以1 km为数轴的单位长度,那么点P的位置就可以用一对数 来表示.
(1)在图中,点Q、E、F相对于点O的位置应分别怎样表示
点Q: ;点E: ;点F: .
(2)(3,-1.5)表示 位置;(-2,2)表示 位置.
(3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗 举例说明.
归纳总结 在平面上画两条 重合、互相 且具有 单位长度的数轴(教材“图17.2.2”),这就建立了平面 .通常把其中水平的一条数轴叫做x轴或 轴,取向 为正方向;铅直的数轴叫做y轴或 轴,取向 为正方向;两数轴的交点O叫做坐标 .
【答案】1.不同
2.首先找到第几排,再找这一排中的第几个座位.
3.两
4.(东3 km,北2 km)
5.(3,2)
(1)(东3 km,北3 km),即Q(3,3) (西2 km,北3 km),即E(-2,3) (西2 km,南1.5 km),即F(-2,-1.5)
(2)旭日大道与团结路交叉口 月光大道与和平路交叉口
(3)把中山路和繁星大道看成数轴后,就相当于把街道图无限延伸了,街道上任何一点都可以用一对数来表示.例如:月光大道和中山路交叉口可以表示为(-2,0).
归纳总结 原点 垂直 相同 直角坐标系 横 右 纵 上 原点
知识点二 点的坐标与象限
阅读本课时教材“回忆”下面至“练习”以上的部分,完成下列填空.
1.建立了平面直角坐标系后,两条坐标轴把平面分成4个区域,分别称为第一、二、三、四象限,坐标轴 (填“是”或“不”)属于任何一个象限.
2.第一象限( , ),第二象限( , ),第三象限( , ),第四象限( , )(填出“+”“-”号).
3.两条坐标轴上的点的坐标特点是:x轴上的点的纵坐标等于 ,反过来,纵坐标等于 的点都在x轴上;y轴上的点的横坐标等于 ,反过来,横坐标等于 的点都在y轴上.
4.若点在第一、三象限的角平分线上,它的 等于 ;若点在第二、四象限的角平分线上,它的横坐标与纵坐标 .
5.若两个点关于x轴对称,则 坐标相等, 坐标互为相反数;若两个点关于y轴对称,则 坐标相等, 坐标互为相反数;若两个点关于原点对称,则横坐标、纵坐标 .
归纳总结 1.在平面直角坐标系中,任意一点都可以用 来表示. 坐标在前, 坐标在后.
2.我们在坐标平面上可以看到:对于平面上的任意一点,都有唯一 (即这个点的坐标)与它对应;反过来,对任意一对有序实数,平面上都有唯一的 与它对应.这就是说,在平面直角坐标系中的 和 也是一一对应的.
【答案】1.不
2.+ + - + - - + -
3.0 0 0 0
4.纵坐标 横坐标 互为相反数
5.横 纵 纵 横 都互为相反数
归纳总结
1.一对有序实数 横 纵
2.一对有序实数 点 点 有序实数对
对点自测 已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P的坐标是 ( )
A.(-3,4) B.(3,4)
C.(-4,3) D.(4,3)
【答案】B
合作探究
任务驱动一 如图,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 .
【答案】(1,2)
任务驱动二 已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且M'到y轴的距离等于4,那么点M'的坐标是 ( )
A.(4,2)或(-4,2)
B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2)
D.(4,-2)或(-1,-2)
变式演练 如图,如果“”所在位置的坐标为(-1,-2),“”所在位置的坐标为(-3,1),那么,“”所在位置的坐标为 .
【答案】B
变式演练 (2,-2)
任务驱动三 (1)点A(2,-3)在第 象限.
(2)若点C(a-1,-b+3)在x轴上,则b= ;若点D(-3a-1,-2b+3)在y轴上,则a= .
(3)点P(5,-3)关于x轴对称的点的坐标是 ;点P(3,-5)关于y轴对称的点的坐标是 ;点P(-2,-4)关于原点对称的点的坐标是 .
【答案】(1)四
(2)3 -
(3)(5,3) (-3,-5) (2,4)
任务驱动四 (1)已知点A与点B(-1,6)关于x轴对称,求点A关于原点对称的点C的坐标.(2)到x轴的距离为2,到y轴的距离为3的点有几个 写出它们的坐标.
方法归纳交流 1.点(a,b)关于x轴、y轴、原点的对称点的坐标分别是 .
2.在坐标系中,点P(a,b)到x轴的距离为 ,到y轴的距离为 .
【答案】解:(1)因为点A与点B(-1,6)关于x轴对称,所以点A(-1,-6),点C(1,6).
(2)在每个象限内都有一个满足条件的点,故有4个点,它们的坐标分别是(3,2)、(-3,2)、(-3,-2)、(3,-2).
方法归纳交流
1.(a,-b)、(-a,b)、(-a,-b)
2.|b| |a|
2
