2023-2024学年初中数学华东师大版八年级下册第17章 函数及其图象 复习课 学案 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第17章 函数及其图象 复习课 学案 (含答案) | 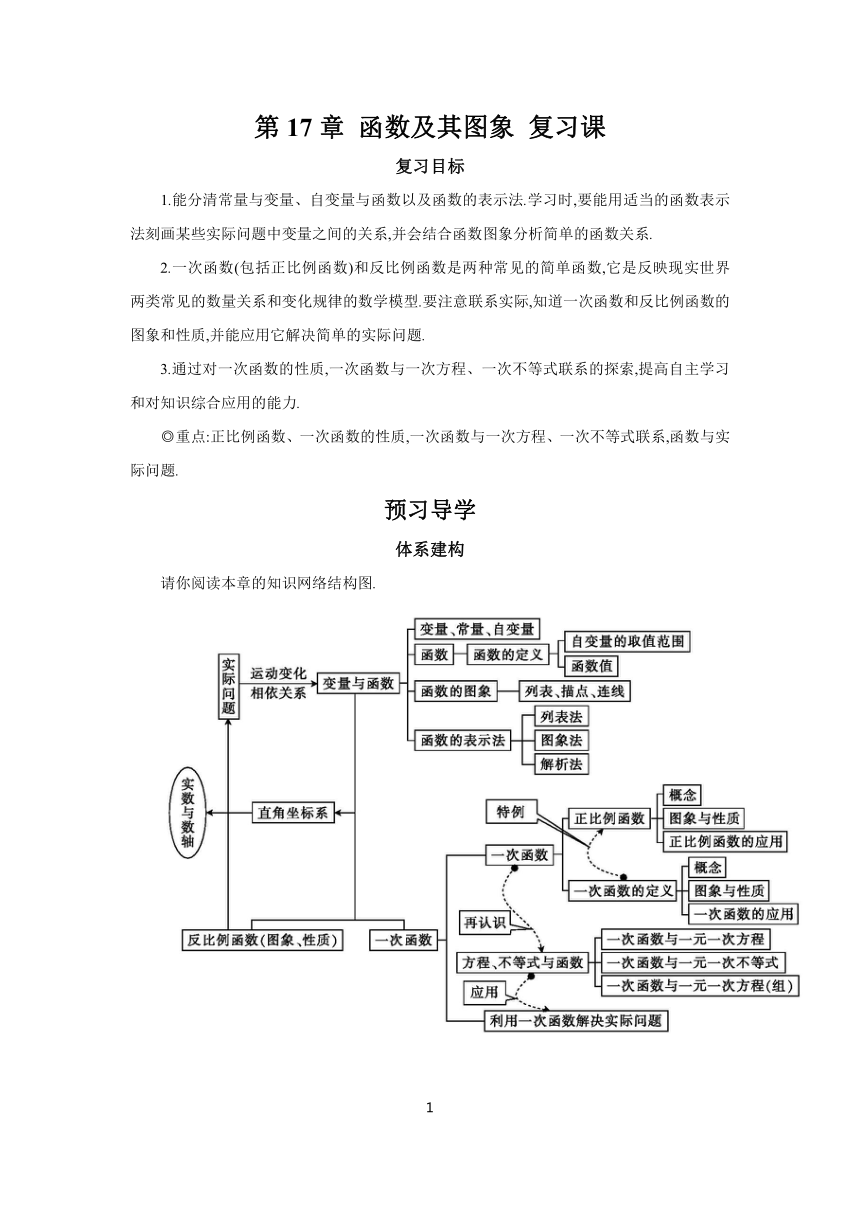 | |
| 格式 | docx | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:53:16 | ||
图片预览




文档简介
第17章 函数及其图象 复习课
复习目标
1.能分清常量与变量、自变量与函数以及函数的表示法.学习时,要能用适当的函数表示法刻画某些实际问题中变量之间的关系,并会结合函数图象分析简单的函数关系.
2.一次函数(包括正比例函数)和反比例函数是两种常见的简单函数,它是反映现实世界两类常见的数量关系和变化规律的数学模型.要注意联系实际,知道一次函数和反比例函数的图象和性质,并能应用它解决简单的实际问题.
3.通过对一次函数的性质,一次函数与一次方程、一次不等式联系的探索,提高自主学习和对知识综合应用的能力.
◎重点:正比例函数、一次函数的性质,一次函数与一次方程、一次不等式联系,函数与实际问题.
预习导学
体系建构
请你阅读本章的知识网络结构图.
核心梳理
1.变量与函数:在某一变化过程中,可以取不同数值的量,叫做 ;数值始终保持不变的量,我们称之为 .
2.表示函数关系的方法通常有三种:(1) ,(2) ,(3) .
3.平面直角坐标系的定义:在平面内画两条互相垂直并且原点重合的数轴,这样就建立了 ,其中水平的数轴叫做 ,垂直的数轴叫做 ,两轴的交点O称为 .
4.直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系.
直线y=kx+b(k≠0) 直线y=kx(k≠0);
当b>0时,把直线y=kx向 平移 个单位长度,可得直线y=kx+b;
当b<0时,把直线y=kx向 平移 个单位长度,可得直线y=kx+b.
5.一般地,如果两个变量x、y之间的关系可表示成 的形式,那么称y是x的反比例函数,反比例函数共有三种表达方式: .
注意:反比例函数的自变量x不能为 .
【答案】核心梳理
1.变量 常量
2.解析法 列表法 图象法
3.平面直角坐标系 x轴或横轴 y轴或纵轴 原点
4.平行 上 b 下 |b|
5.y=(k≠0) xy=k,y=kx-1,y=(k≠0)
0
合作探究
专题一 函数的定义、自变量的取值范围及从图象中获取信息
1.在下列关于x、y两个变量的图象中,不能表示y是x的函数的是 ( )
A B C D
2.在函数y=中,自变量的取值范围是 .
方法归纳交流 在中,x的取值范围是 ,因为在分母上,所以此题中x的取值范围是 .
3.在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别是 、 (填写序号).
(2)请你为剩下的函数图象写出一个合适的情境.
【答案】1.C
2.x>2
方法归纳交流
x>2 x>2
3.解:(1)∵情境a:小芳离开家不久,即离家一段路程,此时①②③都符合,
发现把作业本忘在家里,于是返回了家里找到了作业本,即又返回家,离家的距离是0,此时②③都符合,
又去学校,即离家越来越远,此时只有③返回,
∴只有③符合情境a;
∵情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进,即离家越来越远,且没有停留,
∴只有①符合,故答案为③,①.
(2)情境是小芳离开家不久,休息了一会儿,又走回了家.
专题二 一次函数的图象
4.不论b取什么值,直线y=3x+b必经过 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
5.下列各点,在一次函数y=2x+6的图象上的是 ( )
A.(-5,4) B.(-3.5,1)
C.(4,20) D.(-3,0)
6.如图,下面有三个关系式和三个图象,哪一个关系式与哪一个图象能够表示同一个一次函数
(1)x+y=3;
(2)y=1+x;
(3)y=2x.
方法归纳交流 一次函数y=kx+b中,当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 ;当b=0时,图象过坐标 .
【答案】4.B 5.D
6.解:式子(1)与图2表示同一个函数;式子(2)与图1表示同一个函数;式子(3)与图3表示同一个函数.
方法归纳交流
增大 减少 原点
专题三 一次函数的性质
7.若点(-3,y1)、(2,y2)都在直线y=-x+12上,则y1与y2的大小关系是 ( )
A.y1>y2 B.y1=y2
C.y18.若一次函数y=(4-m)x+2的函数值y随x的增大而减小,则m的取值范围是 ( )
A.m<4 B.m>4
C.m<2 D.m>2
9.已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方
(3)当m、n为何值时,函数图象经过原点
方法归纳交流 本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.它的图象为一条直线,当k>0时,图象经过第 象限,y随x的增大而 ;当k<0时,图象经过第 象限,y随x的增大而 ;当 时,图象与y轴的交点在x轴的上方;当b=0时,图象过坐标 ;当 时,图象与y轴的交点在x轴的下方.
【答案】7.A 8.B
9.解:(1)当6+3m<0,即m<-2,y随x的增大而减小,
所以当m<-2,n为任何实数时,y随x的增大而减小;
(2)当6+3m≠0,n-4<0时,函数的图象与y轴的交点在x轴的下方,
解不等式,得m≠-2,n<4,
所以当m≠2,n<4时,函数的图象与y轴的交点在x轴的下方.
(3)当6+3m≠0,n-4=0,函数图象经过原点,
解不等式、方程,得m≠-2,n=4,
所以当m≠-2,n=4时,函数图象经过原点.
方法归纳交流
一、三 增大 二、四 减小 b>0 原点 b<0
专题四 待定系数法
10.已知一次函数y=kx+5的图象经过点(-1,2),则k= .
11.已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k= ,b= .
12.如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位长度后刚好在反比例函数y=上.
(1)求出一次函数的关系式.
(2)求出反比例函数的关系式.
方法归纳交流 1.把点A、B的坐标分别代入一次函数表达式 中,列出关于 的方程组,通过解方程组来求它们的值即求出一次函数的关系式.
2.将平移后的点A的坐标代入反比例函数表达式 ,解方程即可求得 的值.根据图象信息要注意自变量的取值范围 .
【答案】10.3
11.2 10
12.解:(1)根据图象知,A(-4,0),B(0,2),则
解得所以一次函数关系式是y=x+2.
(2)把点A(-4,0)向上平移1个单位长度后的坐标为(-4,1).
∵平移后的点A正好在反比例函数y=上,∴1=,
解得k2=-4,∴该反比例函数关系式为y=-(x<0).
方法归纳交流
1.y=k1x+b k1、b
2.y= k2 x<0
专题五 一次函数与一次方程、一次不等式的关系
13.已知一次函数y=-x-(a-2),当a 时,函数的图象与y轴的交点在x轴的下方.
14.如图,直线y=ax+b,方程ax+b=1的解x= .
15.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1A.x>1 B.x>2
C.x<1 D.x<2
方法归纳交流 y1【答案】13.>2 14.4 15.C
方法归纳交流
y1=k1x+a y2=k2x+b x
专题六 反比例函数的概念与图象的性质
16.下列函数中,y是x的反比例函数的是 ( )
A.x(y-1)=1
B.y=
C.y=
D.y=
17.已知矩形的面积为8,则它的一组邻边长y与x之间的函数图象大致是 ( )
A B C D
18.在反比例函数y=的图象的每一条曲线上,y都随x的增大而减小,则m的取值范围是 .
方法归纳交流 在反比例函数y=中,当 时,y都随x的增大而减小;当 时,y都随x的增大而增大.
【答案】16.D 17.B
18.m<1
方法归纳交流
k>0 k<0
2
复习目标
1.能分清常量与变量、自变量与函数以及函数的表示法.学习时,要能用适当的函数表示法刻画某些实际问题中变量之间的关系,并会结合函数图象分析简单的函数关系.
2.一次函数(包括正比例函数)和反比例函数是两种常见的简单函数,它是反映现实世界两类常见的数量关系和变化规律的数学模型.要注意联系实际,知道一次函数和反比例函数的图象和性质,并能应用它解决简单的实际问题.
3.通过对一次函数的性质,一次函数与一次方程、一次不等式联系的探索,提高自主学习和对知识综合应用的能力.
◎重点:正比例函数、一次函数的性质,一次函数与一次方程、一次不等式联系,函数与实际问题.
预习导学
体系建构
请你阅读本章的知识网络结构图.
核心梳理
1.变量与函数:在某一变化过程中,可以取不同数值的量,叫做 ;数值始终保持不变的量,我们称之为 .
2.表示函数关系的方法通常有三种:(1) ,(2) ,(3) .
3.平面直角坐标系的定义:在平面内画两条互相垂直并且原点重合的数轴,这样就建立了 ,其中水平的数轴叫做 ,垂直的数轴叫做 ,两轴的交点O称为 .
4.直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系.
直线y=kx+b(k≠0) 直线y=kx(k≠0);
当b>0时,把直线y=kx向 平移 个单位长度,可得直线y=kx+b;
当b<0时,把直线y=kx向 平移 个单位长度,可得直线y=kx+b.
5.一般地,如果两个变量x、y之间的关系可表示成 的形式,那么称y是x的反比例函数,反比例函数共有三种表达方式: .
注意:反比例函数的自变量x不能为 .
【答案】核心梳理
1.变量 常量
2.解析法 列表法 图象法
3.平面直角坐标系 x轴或横轴 y轴或纵轴 原点
4.平行 上 b 下 |b|
5.y=(k≠0) xy=k,y=kx-1,y=(k≠0)
0
合作探究
专题一 函数的定义、自变量的取值范围及从图象中获取信息
1.在下列关于x、y两个变量的图象中,不能表示y是x的函数的是 ( )
A B C D
2.在函数y=中,自变量的取值范围是 .
方法归纳交流 在中,x的取值范围是 ,因为在分母上,所以此题中x的取值范围是 .
3.在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别是 、 (填写序号).
(2)请你为剩下的函数图象写出一个合适的情境.
【答案】1.C
2.x>2
方法归纳交流
x>2 x>2
3.解:(1)∵情境a:小芳离开家不久,即离家一段路程,此时①②③都符合,
发现把作业本忘在家里,于是返回了家里找到了作业本,即又返回家,离家的距离是0,此时②③都符合,
又去学校,即离家越来越远,此时只有③返回,
∴只有③符合情境a;
∵情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进,即离家越来越远,且没有停留,
∴只有①符合,故答案为③,①.
(2)情境是小芳离开家不久,休息了一会儿,又走回了家.
专题二 一次函数的图象
4.不论b取什么值,直线y=3x+b必经过 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
5.下列各点,在一次函数y=2x+6的图象上的是 ( )
A.(-5,4) B.(-3.5,1)
C.(4,20) D.(-3,0)
6.如图,下面有三个关系式和三个图象,哪一个关系式与哪一个图象能够表示同一个一次函数
(1)x+y=3;
(2)y=1+x;
(3)y=2x.
方法归纳交流 一次函数y=kx+b中,当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 ;当b=0时,图象过坐标 .
【答案】4.B 5.D
6.解:式子(1)与图2表示同一个函数;式子(2)与图1表示同一个函数;式子(3)与图3表示同一个函数.
方法归纳交流
增大 减少 原点
专题三 一次函数的性质
7.若点(-3,y1)、(2,y2)都在直线y=-x+12上,则y1与y2的大小关系是 ( )
A.y1>y2 B.y1=y2
C.y1
A.m<4 B.m>4
C.m<2 D.m>2
9.已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方
(3)当m、n为何值时,函数图象经过原点
方法归纳交流 本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.它的图象为一条直线,当k>0时,图象经过第 象限,y随x的增大而 ;当k<0时,图象经过第 象限,y随x的增大而 ;当 时,图象与y轴的交点在x轴的上方;当b=0时,图象过坐标 ;当 时,图象与y轴的交点在x轴的下方.
【答案】7.A 8.B
9.解:(1)当6+3m<0,即m<-2,y随x的增大而减小,
所以当m<-2,n为任何实数时,y随x的增大而减小;
(2)当6+3m≠0,n-4<0时,函数的图象与y轴的交点在x轴的下方,
解不等式,得m≠-2,n<4,
所以当m≠2,n<4时,函数的图象与y轴的交点在x轴的下方.
(3)当6+3m≠0,n-4=0,函数图象经过原点,
解不等式、方程,得m≠-2,n=4,
所以当m≠-2,n=4时,函数图象经过原点.
方法归纳交流
一、三 增大 二、四 减小 b>0 原点 b<0
专题四 待定系数法
10.已知一次函数y=kx+5的图象经过点(-1,2),则k= .
11.已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k= ,b= .
12.如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位长度后刚好在反比例函数y=上.
(1)求出一次函数的关系式.
(2)求出反比例函数的关系式.
方法归纳交流 1.把点A、B的坐标分别代入一次函数表达式 中,列出关于 的方程组,通过解方程组来求它们的值即求出一次函数的关系式.
2.将平移后的点A的坐标代入反比例函数表达式 ,解方程即可求得 的值.根据图象信息要注意自变量的取值范围 .
【答案】10.3
11.2 10
12.解:(1)根据图象知,A(-4,0),B(0,2),则
解得所以一次函数关系式是y=x+2.
(2)把点A(-4,0)向上平移1个单位长度后的坐标为(-4,1).
∵平移后的点A正好在反比例函数y=上,∴1=,
解得k2=-4,∴该反比例函数关系式为y=-(x<0).
方法归纳交流
1.y=k1x+b k1、b
2.y= k2 x<0
专题五 一次函数与一次方程、一次不等式的关系
13.已知一次函数y=-x-(a-2),当a 时,函数的图象与y轴的交点在x轴的下方.
14.如图,直线y=ax+b,方程ax+b=1的解x= .
15.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1
C.x<1 D.x<2
方法归纳交流 y1
方法归纳交流
y1=k1x+a y2=k2x+b x
专题六 反比例函数的概念与图象的性质
16.下列函数中,y是x的反比例函数的是 ( )
A.x(y-1)=1
B.y=
C.y=
D.y=
17.已知矩形的面积为8,则它的一组邻边长y与x之间的函数图象大致是 ( )
A B C D
18.在反比例函数y=的图象的每一条曲线上,y都随x的增大而减小,则m的取值范围是 .
方法归纳交流 在反比例函数y=中,当 时,y都随x的增大而减小;当 时,y都随x的增大而增大.
【答案】16.D 17.B
18.m<1
方法归纳交流
k>0 k<0
2
