2023-2024学年初中数学华东师大版八年级下册第19章 矩形、菱形与正方形 复习课 学案 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第19章 矩形、菱形与正方形 复习课 学案 (含答案) | 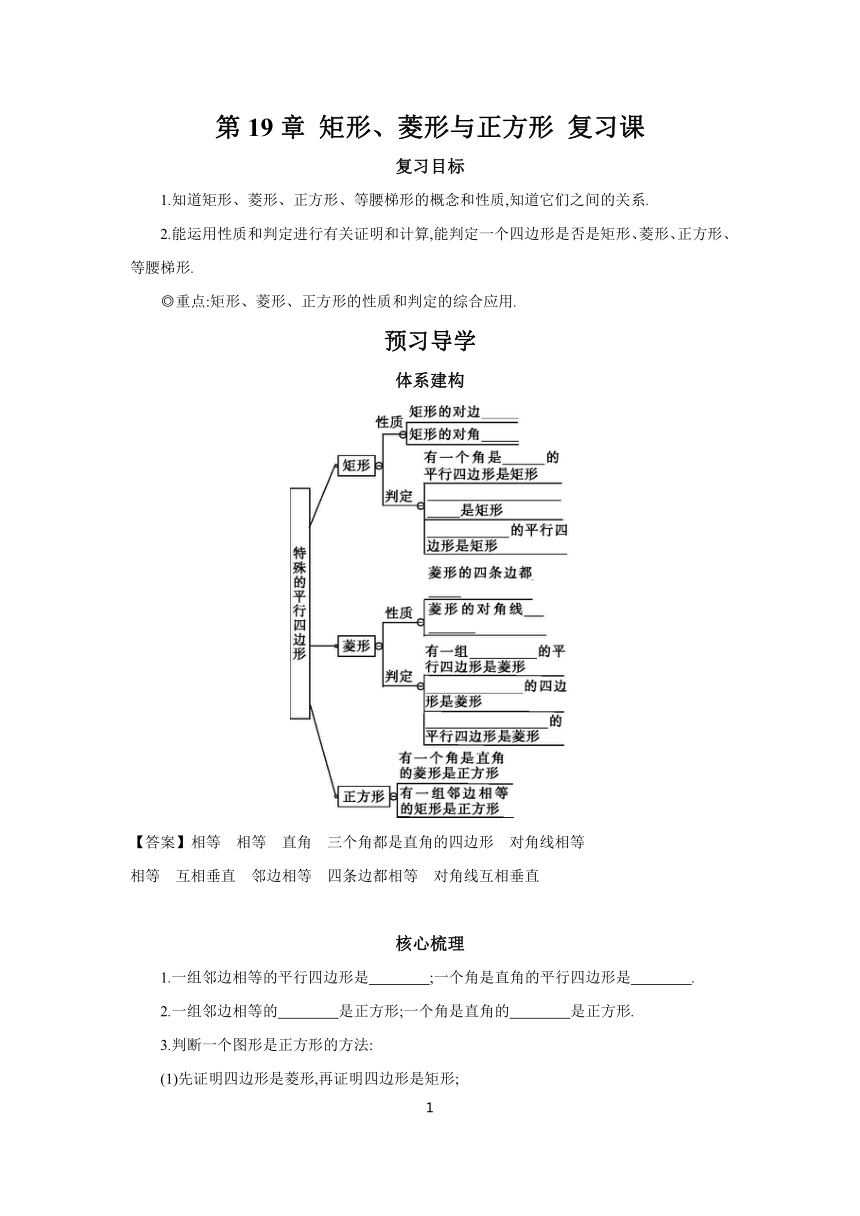 | |
| 格式 | docx | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:54:06 | ||
图片预览


文档简介
第19章 矩形、菱形与正方形 复习课
复习目标
1.知道矩形、菱形、正方形、等腰梯形的概念和性质,知道它们之间的关系.
2.能运用性质和判定进行有关证明和计算,能判定一个四边形是否是矩形、菱形、正方形、等腰梯形.
◎重点:矩形、菱形、正方形的性质和判定的综合应用.
预习导学
体系建构
【答案】相等 相等 直角 三个角都是直角的四边形 对角线相等
相等 互相垂直 邻边相等 四条边都相等 对角线互相垂直
核心梳理
1.一组邻边相等的平行四边形是 ;一个角是直角的平行四边形是 .
2.一组邻边相等的 是正方形;一个角是直角的 是正方形.
3.判断一个图形是正方形的方法:
(1)先证明四边形是菱形,再证明四边形是矩形;
(2)先证明四边形是矩形,再证明四边形是菱形.
【答案】1.菱形 矩形
2.矩形 菱形
合作探究
专题一 矩形的性质和判定
1.如图,在矩形ABCD中,E是BC的中点,矩形ABCD的周长是20 cm,AE=5 cm,则AB的长为 cm.
2.如图,在△ABC中,点D在AB上,AD=BD=CD且DE、DF分别平分∠BDC、∠ADC.
求证:四边形CEDF是矩形.
方法归纳交流 矩形的判定中,除了“对角线相等的平行四边形是矩形”外,其他判定都需要满足一个角是直角.
【答案】1.4
2.证明:∵DE、DF分别平分∠BDC、∠ADC,
∴∠FDC=∠ADC,∠CDE=∠BDC.∵∠ADB=180°,∴∠EDF=90°.∵AD=BD=CD,∴∠A=∠ACD,∠B=∠BCD.∵∠A+∠B+∠ACB=180°,∴∠ACB=90°.∵DA=DC,DF平分∠ADC,∴DF⊥AC,∴四边形CEDF是矩形.
专题二 菱形的性质和判定
3.如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC∶BD=1∶2,则AO∶BO= ,菱形ABCD的面积S= .
4.如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于点E.
(1)请你判断四边形OCED的形状,并说明理由.
(2)若AB=6,BC=8,求四边形OCED的面积.
【答案】3.1∶2 16
4.解:(1)四边形OCED的形状是菱形.
理由如下:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形.
∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OD=OC,∴四边形CODE是菱形.
(2)∵AB=6,BC=8,∴矩形ABCD的面积=6×8=48.
∵S△ODC=S矩形ABCD=12,∴四边形OCED的面积=2S△ODC=24.
专题三 正方形的性质和判定
5.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
6.如图,点A'、B'、C'、D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.求证:四边形A'B'C'D'为正方形.
方法归纳交流 注意全等三角形的性质在正方形的判定中的应用.
【答案】5.D
6.证明:∵四边形ABCD为正方形,∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.又∵AA'=BB'=CC'=DD',∴D'A=A'B=B'C=C'D,∴D'A'=A'B'=B'C'=C'D'.∵△AA'D'≌△DD'C'.∴∠AD'A'=∠DC'D'.∵∠DD'C'+∠DC'D'=90°,∴∠DD'C'+∠AD'A'=90°,∴∠A'D'C'=180°-(∠DD'C'+∠AD'A')=90°,∴四边形A'B'C'D'为正方形.
专题四 各种判定方法、性质的综合应用
7.如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是 ( )
A.BE=AF
B.∠DAF=∠BEC
C.∠AFB+∠BEC=90°
D.AG⊥BE
8.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形.(只写结论,不需证明)
【答案】7.C
8.解:(1)证明:在矩形ABCD中,AB=CD,∠A=∠D=90°.
又∵M是AD的中点,∴AM=DM,∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:E、F、N分别是BM、CM、CB的中点,∴NF∥ME,NF=ME,
∴四边形MENF是平行四边形.由(1)得BM=CM,∴ME=MF,∴ MENF是菱形.
(3)2∶1.
2
复习目标
1.知道矩形、菱形、正方形、等腰梯形的概念和性质,知道它们之间的关系.
2.能运用性质和判定进行有关证明和计算,能判定一个四边形是否是矩形、菱形、正方形、等腰梯形.
◎重点:矩形、菱形、正方形的性质和判定的综合应用.
预习导学
体系建构
【答案】相等 相等 直角 三个角都是直角的四边形 对角线相等
相等 互相垂直 邻边相等 四条边都相等 对角线互相垂直
核心梳理
1.一组邻边相等的平行四边形是 ;一个角是直角的平行四边形是 .
2.一组邻边相等的 是正方形;一个角是直角的 是正方形.
3.判断一个图形是正方形的方法:
(1)先证明四边形是菱形,再证明四边形是矩形;
(2)先证明四边形是矩形,再证明四边形是菱形.
【答案】1.菱形 矩形
2.矩形 菱形
合作探究
专题一 矩形的性质和判定
1.如图,在矩形ABCD中,E是BC的中点,矩形ABCD的周长是20 cm,AE=5 cm,则AB的长为 cm.
2.如图,在△ABC中,点D在AB上,AD=BD=CD且DE、DF分别平分∠BDC、∠ADC.
求证:四边形CEDF是矩形.
方法归纳交流 矩形的判定中,除了“对角线相等的平行四边形是矩形”外,其他判定都需要满足一个角是直角.
【答案】1.4
2.证明:∵DE、DF分别平分∠BDC、∠ADC,
∴∠FDC=∠ADC,∠CDE=∠BDC.∵∠ADB=180°,∴∠EDF=90°.∵AD=BD=CD,∴∠A=∠ACD,∠B=∠BCD.∵∠A+∠B+∠ACB=180°,∴∠ACB=90°.∵DA=DC,DF平分∠ADC,∴DF⊥AC,∴四边形CEDF是矩形.
专题二 菱形的性质和判定
3.如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC∶BD=1∶2,则AO∶BO= ,菱形ABCD的面积S= .
4.如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于点E.
(1)请你判断四边形OCED的形状,并说明理由.
(2)若AB=6,BC=8,求四边形OCED的面积.
【答案】3.1∶2 16
4.解:(1)四边形OCED的形状是菱形.
理由如下:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形.
∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD,∴OD=OC,∴四边形CODE是菱形.
(2)∵AB=6,BC=8,∴矩形ABCD的面积=6×8=48.
∵S△ODC=S矩形ABCD=12,∴四边形OCED的面积=2S△ODC=24.
专题三 正方形的性质和判定
5.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
6.如图,点A'、B'、C'、D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.求证:四边形A'B'C'D'为正方形.
方法归纳交流 注意全等三角形的性质在正方形的判定中的应用.
【答案】5.D
6.证明:∵四边形ABCD为正方形,∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.又∵AA'=BB'=CC'=DD',∴D'A=A'B=B'C=C'D,∴D'A'=A'B'=B'C'=C'D'.∵△AA'D'≌△DD'C'.∴∠AD'A'=∠DC'D'.∵∠DD'C'+∠DC'D'=90°,∴∠DD'C'+∠AD'A'=90°,∴∠A'D'C'=180°-(∠DD'C'+∠AD'A')=90°,∴四边形A'B'C'D'为正方形.
专题四 各种判定方法、性质的综合应用
7.如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是 ( )
A.BE=AF
B.∠DAF=∠BEC
C.∠AFB+∠BEC=90°
D.AG⊥BE
8.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形.(只写结论,不需证明)
【答案】7.C
8.解:(1)证明:在矩形ABCD中,AB=CD,∠A=∠D=90°.
又∵M是AD的中点,∴AM=DM,∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:E、F、N分别是BM、CM、CB的中点,∴NF∥ME,NF=ME,
∴四边形MENF是平行四边形.由(1)得BM=CM,∴ME=MF,∴ MENF是菱形.
(3)2∶1.
2
