2023-2024学年初中数学华东师大版八年级下册第20章 数据的整理与初步处理 复习课 学案(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第20章 数据的整理与初步处理 复习课 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:54:31 | ||
图片预览

文档简介
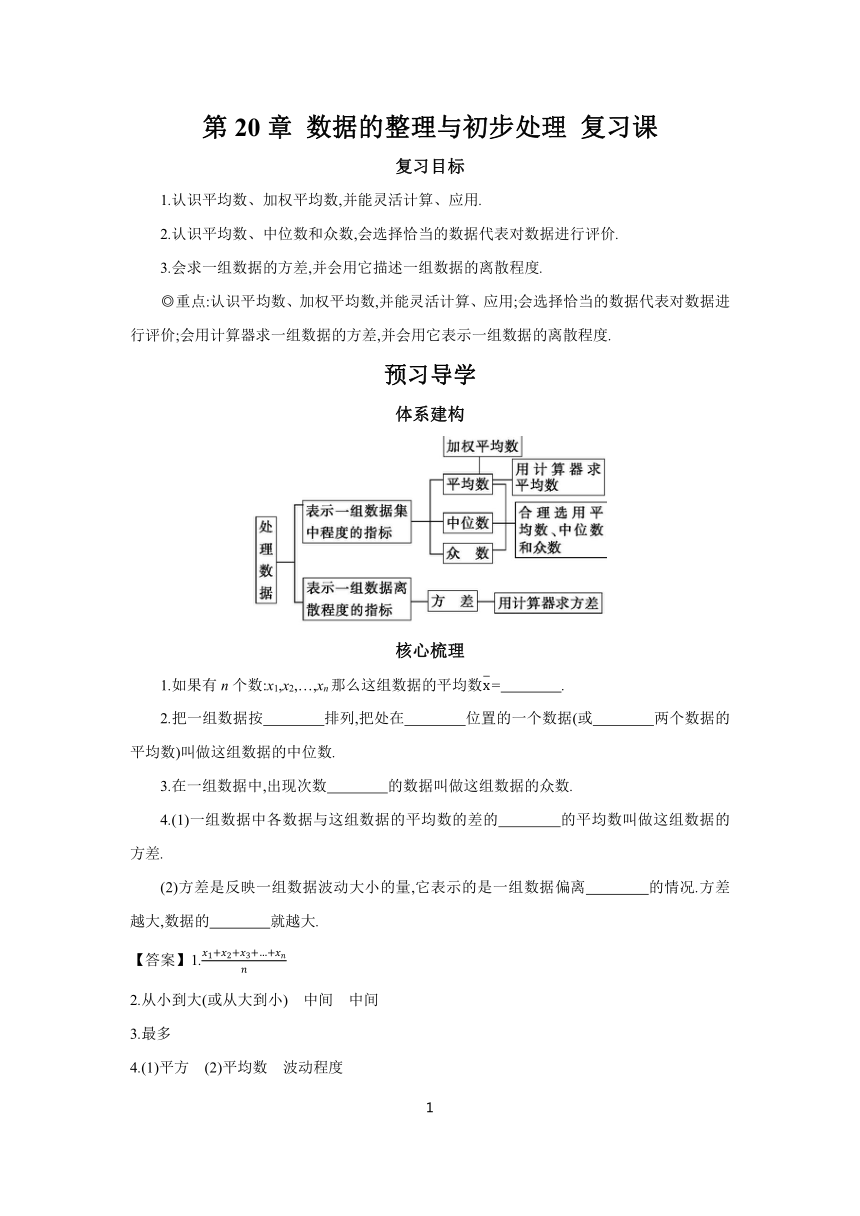
第20章 数据的整理与初步处理 复习课
复习目标
1.认识平均数、加权平均数,并能灵活计算、应用.
2.认识平均数、中位数和众数,会选择恰当的数据代表对数据进行评价.
3.会求一组数据的方差,并会用它描述一组数据的离散程度.
◎重点:认识平均数、加权平均数,并能灵活计算、应用;会选择恰当的数据代表对数据进行评价;会用计算器求一组数据的方差,并会用它表示一组数据的离散程度.
预习导学
体系建构
核心梳理
1.如果有n个数:x1,x2,…,xn那么这组数据的平均数= .
2.把一组数据按 排列,把处在 位置的一个数据(或 两个数据的平均数)叫做这组数据的中位数.
3.在一组数据中,出现次数 的数据叫做这组数据的众数.
4.(1)一组数据中各数据与这组数据的平均数的差的 的平均数叫做这组数据的方差.
(2)方差是反映一组数据波动大小的量,它表示的是一组数据偏离 的情况.方差越大,数据的 就越大.
【答案】1.
2.从小到大(或从大到小) 中间 中间
3.最多
4.(1)平方 (2)平均数 波动程度
合作探究
专题一 平均数、中位数和众数的选用
1.小亮和小莹自制了一个标靶进行投标比赛,两人各投了10次,如图所示的是他们投标成绩的统计图.
(1)根据图中信息计算小亮与小莹的平均数、中位数、众数.
(2)分别用平均数和中位数解释谁的成绩比较好.
方法归纳交流 平均数、中位数、众数都可以作为一组数据的代表,其中 能够从总体角度代表数据; 能反映数据的居中信息; 代表出现次数最多的数据.
【答案】1.解:(1)根据题意得小亮的环数为9,5,7,8,7,6,8,6,7,7.
平均数为(9+5+7+8+7+6+8+6+7+7)=7,中位数为7,众数为7;
小莹的环数为3,4,6,9,5,7,8,9,9,10.
平均数为(3+4+6+9+5+7+8+9+9+10)=7,中位数为7.5,众数为9.
(2)平均数相等说明:两人整体水平相当,成绩一样好;小莹的中位数大说明:小莹的成绩比小亮好.
方法归纳交流
平均数 中位数 众数
专题二 方差的计算与应用
2.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩(单位:环)如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲、乙的平均成绩.
(2)分别计算甲、乙六次测试成绩的方差.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
方法归纳交流 方差能够反映数据的波动大小,方差越小,数据的波动就 当两组数据的平均数相同时,我们常常根据 的大小来选取.
【答案】2.解:(1)甲的平均成绩:(10+8+9+8+10+9)÷6=9.
乙的平均成绩:(10+7+10+10+9+8)÷6=9.
(2)=[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]
=(1+1+0+1+1+0)=.
=[(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2]
=(1+4+1+1+0+1)=.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
方法归纳交流
越小 方差
2
复习目标
1.认识平均数、加权平均数,并能灵活计算、应用.
2.认识平均数、中位数和众数,会选择恰当的数据代表对数据进行评价.
3.会求一组数据的方差,并会用它描述一组数据的离散程度.
◎重点:认识平均数、加权平均数,并能灵活计算、应用;会选择恰当的数据代表对数据进行评价;会用计算器求一组数据的方差,并会用它表示一组数据的离散程度.
预习导学
体系建构
核心梳理
1.如果有n个数:x1,x2,…,xn那么这组数据的平均数= .
2.把一组数据按 排列,把处在 位置的一个数据(或 两个数据的平均数)叫做这组数据的中位数.
3.在一组数据中,出现次数 的数据叫做这组数据的众数.
4.(1)一组数据中各数据与这组数据的平均数的差的 的平均数叫做这组数据的方差.
(2)方差是反映一组数据波动大小的量,它表示的是一组数据偏离 的情况.方差越大,数据的 就越大.
【答案】1.
2.从小到大(或从大到小) 中间 中间
3.最多
4.(1)平方 (2)平均数 波动程度
合作探究
专题一 平均数、中位数和众数的选用
1.小亮和小莹自制了一个标靶进行投标比赛,两人各投了10次,如图所示的是他们投标成绩的统计图.
(1)根据图中信息计算小亮与小莹的平均数、中位数、众数.
(2)分别用平均数和中位数解释谁的成绩比较好.
方法归纳交流 平均数、中位数、众数都可以作为一组数据的代表,其中 能够从总体角度代表数据; 能反映数据的居中信息; 代表出现次数最多的数据.
【答案】1.解:(1)根据题意得小亮的环数为9,5,7,8,7,6,8,6,7,7.
平均数为(9+5+7+8+7+6+8+6+7+7)=7,中位数为7,众数为7;
小莹的环数为3,4,6,9,5,7,8,9,9,10.
平均数为(3+4+6+9+5+7+8+9+9+10)=7,中位数为7.5,众数为9.
(2)平均数相等说明:两人整体水平相当,成绩一样好;小莹的中位数大说明:小莹的成绩比小亮好.
方法归纳交流
平均数 中位数 众数
专题二 方差的计算与应用
2.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩(单位:环)如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲 10 8 9 8 10 9
乙 10 7 10 10 9 8
(1)根据表格中的数据,计算出甲、乙的平均成绩.
(2)分别计算甲、乙六次测试成绩的方差.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
方法归纳交流 方差能够反映数据的波动大小,方差越小,数据的波动就 当两组数据的平均数相同时,我们常常根据 的大小来选取.
【答案】2.解:(1)甲的平均成绩:(10+8+9+8+10+9)÷6=9.
乙的平均成绩:(10+7+10+10+9+8)÷6=9.
(2)=[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]
=(1+1+0+1+1+0)=.
=[(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2]
=(1+4+1+1+0+1)=.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
方法归纳交流
越小 方差
2
