第三章平面上直线的位置关系和度量关系复习(二)(题目无答案)
文档属性
| 名称 | 第三章平面上直线的位置关系和度量关系复习(二)(题目无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-08 08:11:00 | ||
图片预览

文档简介
一、梳理知识:
(一)平行线:
1、平面上两条直线的位置关系: 、 、 。
2、平行线的概念:同一平面内没有 的两条直线叫做平行线。
3、关于平行线的几个结论:
平行公理:过直线外一点 与已知直线平行。
平行线的传递性:如果两条直线都与第三条直线 ,那么这两条直线也
。
设 a、b、c 是三条直线,如 a∥b, b∥ c, 则 。
4、平行线的性质与判定:
平 行 线 的 性 质 平 行 线 的 判 定
同位角相等
两直线平行 两直线平行
同旁内角互补
因为:AB∥CD
A 1 B 所以 ∠1=∠2 A 1 B 因 ∠1=∠2 所以AB∥CD
3 4 所以AB∥CD
C 4 2 D C 2 3 D =180°所以AB∥CD
°
5、归纳判断两直线平行的方法:
(1)三条判定定理 (2)平行线的概念 (3)平行线的传递性 (4)垂线的性质一
(二)关于垂线:
1、概念:
两直线相交如有一角是 ,这两条直线叫做 。
点到直线的距离是指 的长度。
两平行线间的距离是指两平行线的 。
叫两平行线的公垂线段。
2、 垂线的性质:
(1)在平面内,垂直于同一条直线的两条直线
(2)在平面内,若一直线垂直于两条 中的一条,则这条直线
必 另一条。
(3)在平面内,过一点 与已知直线垂直。
(4)直线外一点与直线上各点连结的所有线段中, 最短。
(5)两平行线的所有公垂线段都 。或两平行线间的距离处处 。
二、规律方法探索:
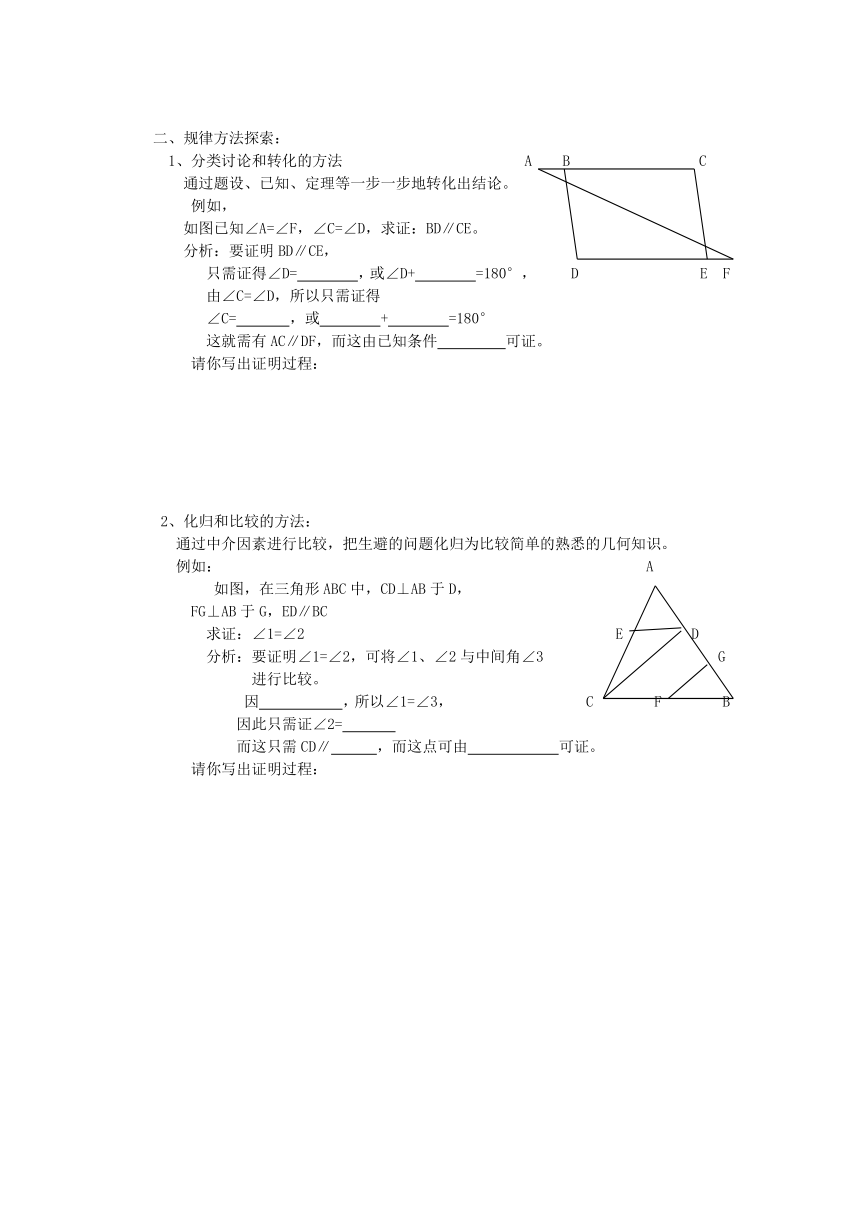
1、分类讨论和转化的方法 A B C
通过题设、已知、定理等一步一步地转化出结论。
例如,
如图已知∠A=∠F,∠C=∠D,求证:BD∥CE。
分析:要证明BD∥CE,
只需证得∠D= ,或∠D+ =180°, D E F
由∠C=∠D,所以只需证得
∠C= ,或 + =180°
这就需有AC∥DF,而这由已知条件 可证。
请你写出证明过程:
2、化归和比较的方法:
通过中介因素进行比较,把生避的问题化归为比较简单的熟悉的几何知识。
例如: A
如图,在三角形ABC中,CD⊥AB于D,
FG⊥AB于G,ED∥BC
求证:∠1=∠2 E D
分析:要证明∠1=∠2,可将∠1、∠2与中间角∠3 G
进行比较。
因 ,所以∠1=∠3, C F B
因此只需证∠2=
而这只需CD∥ ,而这点可由 可证。
请你写出证明过程:
三、做一做:
一、相信你的选择(每题3分,共24分)
1.邻补角是指( )
A.和为的两个角 B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角。
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段 B.直线外一点到这条直线的垂线段的长度
C.直线外一点与这条直线上任一点所连接的线段
D.直线外一点与这条直线上任一点所连接的线段的长度
3.在同一平面内,两条直线的位置关系是( )
A.平行或垂直 B.平行或相交 C.垂直或相交 D.平行、垂直或相交
4.在同一平面内有三条直线,如果其中有两条且只有两条平行,那么它们( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
5.在同一平面内,直线,相交于点,又,则直线和的位置关系是( )
A.平行 B.相交 C.垂直 D.平行或垂直
二、试试你的身手(每题3分,共24分)
1.如图1,已知,则_____,_____.
2.两个邻补角的角平分线的位置关系是__ ___.
3.如图2,在中,,,图中与互余的角有_____个.
4.如图3,已知直线相交于点,平分,,,则_____,_____,_____.
5.如图4,若,则_____;若,则_____;若,则_____.(填平行线)
三、挑战你的技能(共52分)
3、如图 已知AB∥CD,BE∥AD,∠DCE=78°
求∠A、∠B、∠D的度数。
2.如图14,,为的中点.
(1)过作,与交于点;
(2)与平行吗?为什么?
A
如图,已知∠1+∠2= 180°, 3=∠B,
试判断∠AED与∠ACB的关系,请说明理由。
D 3 E
F 1
B G C
如图,把一张长方形ABCD沿EF折叠,若∠EFG=50°,
求 ∠DGC、∠BGD的度数。 E
A D
G
B F C
D′ C′
3、举出日常生活中利用“垂线段最短”的例子。(测量跳远的成绩、在地面上测量三角形地形的一边上的高、测量楼上到地面的距离等。)
四、范例分析
(先引导学生分析,然后写出解答。)
解:(1)因为 AB∥CD(已知)
所以 ∠B=∠DCE(两直线平行,同位角相等)
又因为 ∠DCE=78°(已知)
所以 ∠B=78°(等量代换)。
(2)因为 AD∥BE(已知)
所以 ∠B+∠A=180°(两直线平行,同旁内角互补)
又因为 ∠B=78°(已证)
所以 ∠A=180°-78°=102°(等式的性质)。
(3)因为 AD∥BE(已知)
所以 ∠D=∠DCE(两直线平行,内错角相等)
又因为 ∠DCE=78°(已知)
所以 ∠D=78°(等量代换)。
}+
图4
图2
图3
图1
图8
图14
(一)平行线:
1、平面上两条直线的位置关系: 、 、 。
2、平行线的概念:同一平面内没有 的两条直线叫做平行线。
3、关于平行线的几个结论:
平行公理:过直线外一点 与已知直线平行。
平行线的传递性:如果两条直线都与第三条直线 ,那么这两条直线也
。
设 a、b、c 是三条直线,如 a∥b, b∥ c, 则 。
4、平行线的性质与判定:
平 行 线 的 性 质 平 行 线 的 判 定
同位角相等
两直线平行 两直线平行
同旁内角互补
因为:AB∥CD
A 1 B 所以 ∠1=∠2 A 1 B 因 ∠1=∠2 所以AB∥CD
3 4 所以AB∥CD
C 4 2 D C 2 3 D =180°所以AB∥CD
°
5、归纳判断两直线平行的方法:
(1)三条判定定理 (2)平行线的概念 (3)平行线的传递性 (4)垂线的性质一
(二)关于垂线:
1、概念:
两直线相交如有一角是 ,这两条直线叫做 。
点到直线的距离是指 的长度。
两平行线间的距离是指两平行线的 。
叫两平行线的公垂线段。
2、 垂线的性质:
(1)在平面内,垂直于同一条直线的两条直线
(2)在平面内,若一直线垂直于两条 中的一条,则这条直线
必 另一条。
(3)在平面内,过一点 与已知直线垂直。
(4)直线外一点与直线上各点连结的所有线段中, 最短。
(5)两平行线的所有公垂线段都 。或两平行线间的距离处处 。
二、规律方法探索:
1、分类讨论和转化的方法 A B C
通过题设、已知、定理等一步一步地转化出结论。
例如,
如图已知∠A=∠F,∠C=∠D,求证:BD∥CE。
分析:要证明BD∥CE,
只需证得∠D= ,或∠D+ =180°, D E F
由∠C=∠D,所以只需证得
∠C= ,或 + =180°
这就需有AC∥DF,而这由已知条件 可证。
请你写出证明过程:
2、化归和比较的方法:
通过中介因素进行比较,把生避的问题化归为比较简单的熟悉的几何知识。
例如: A
如图,在三角形ABC中,CD⊥AB于D,
FG⊥AB于G,ED∥BC
求证:∠1=∠2 E D
分析:要证明∠1=∠2,可将∠1、∠2与中间角∠3 G
进行比较。
因 ,所以∠1=∠3, C F B
因此只需证∠2=
而这只需CD∥ ,而这点可由 可证。
请你写出证明过程:
三、做一做:
一、相信你的选择(每题3分,共24分)
1.邻补角是指( )
A.和为的两个角 B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角。
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段 B.直线外一点到这条直线的垂线段的长度
C.直线外一点与这条直线上任一点所连接的线段
D.直线外一点与这条直线上任一点所连接的线段的长度
3.在同一平面内,两条直线的位置关系是( )
A.平行或垂直 B.平行或相交 C.垂直或相交 D.平行、垂直或相交
4.在同一平面内有三条直线,如果其中有两条且只有两条平行,那么它们( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
5.在同一平面内,直线,相交于点,又,则直线和的位置关系是( )
A.平行 B.相交 C.垂直 D.平行或垂直
二、试试你的身手(每题3分,共24分)
1.如图1,已知,则_____,_____.
2.两个邻补角的角平分线的位置关系是__ ___.
3.如图2,在中,,,图中与互余的角有_____个.
4.如图3,已知直线相交于点,平分,,,则_____,_____,_____.
5.如图4,若,则_____;若,则_____;若,则_____.(填平行线)
三、挑战你的技能(共52分)
3、如图 已知AB∥CD,BE∥AD,∠DCE=78°
求∠A、∠B、∠D的度数。
2.如图14,,为的中点.
(1)过作,与交于点;
(2)与平行吗?为什么?
A
如图,已知∠1+∠2= 180°, 3=∠B,
试判断∠AED与∠ACB的关系,请说明理由。
D 3 E
F 1
B G C
如图,把一张长方形ABCD沿EF折叠,若∠EFG=50°,
求 ∠DGC、∠BGD的度数。 E
A D
G
B F C
D′ C′
3、举出日常生活中利用“垂线段最短”的例子。(测量跳远的成绩、在地面上测量三角形地形的一边上的高、测量楼上到地面的距离等。)
四、范例分析
(先引导学生分析,然后写出解答。)
解:(1)因为 AB∥CD(已知)
所以 ∠B=∠DCE(两直线平行,同位角相等)
又因为 ∠DCE=78°(已知)
所以 ∠B=78°(等量代换)。
(2)因为 AD∥BE(已知)
所以 ∠B+∠A=180°(两直线平行,同旁内角互补)
又因为 ∠B=78°(已证)
所以 ∠A=180°-78°=102°(等式的性质)。
(3)因为 AD∥BE(已知)
所以 ∠D=∠DCE(两直线平行,内错角相等)
又因为 ∠DCE=78°(已知)
所以 ∠D=78°(等量代换)。
}+
图4
图2
图3
图1
图8
图14
