广东省江门市新会尚雅学校2023-2024学年九年级下学期开学考试数学试题(无答案)
文档属性
| 名称 | 广东省江门市新会尚雅学校2023-2024学年九年级下学期开学考试数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 729.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 20:59:56 | ||
图片预览

文档简介
2023-2024学年第二学期
九年级数学期初大练习(B)
一、选择题
1.在实数,,,3.14中,无理数是( )
A. B. C. D.3.14
2.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3.在下列二次根式中,的取值范围是的是( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.不透明的盒子放有三张大小、形状及质地相同的卡片,卡片上分别写有李白《峨眉山月歌》,李白《渡荆门送别》和王维《寄荆州张丞相》三首诗,小明从盒子中随机抽取两张卡片,卡片上诗的作者都是李白的概率是( )
A. B. C. D.
6.不等式组的解集在数轴上表示为( )
A. B.
C. D.
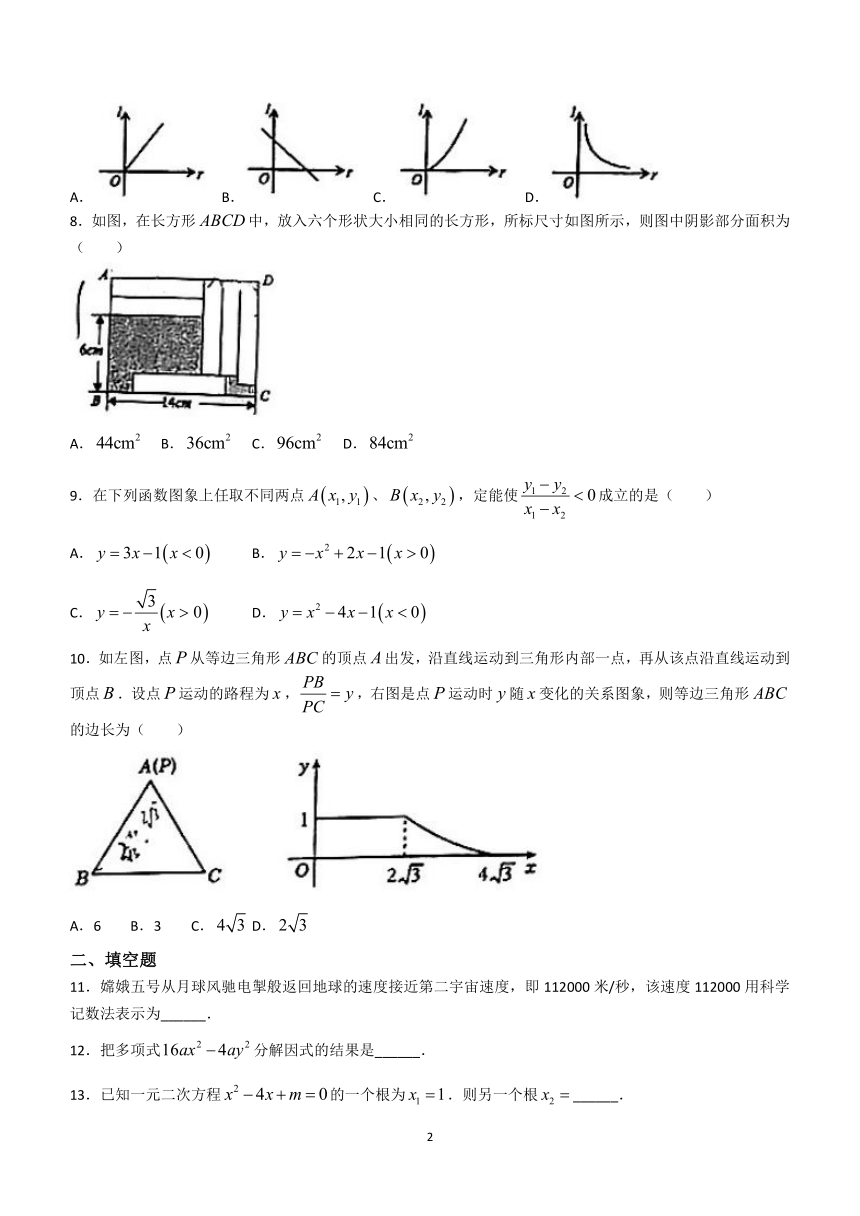
7.若一个圆锥侧面展开图的圆心角是270°,圆锥母线与底面半径之间的函数关系图象大致是( )
A. B. C. D.
8.如图,在长方形中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A. B. C. D.
9.在下列函数图象上任取不同两点、,定能使成立的是( )
A. B.
C. D.
10.如左图,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点.设点运动的路程为,,右图是点运动时随变化的关系图象,则等边三角形的边长为( )
A.6 B.3 C. D.
二、填空题
11.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,该速度112000用科学记数法表示为______.
12.把多项式分解因式的结果是______.
13.已知一元二次方程的一个根为.则另一个根______.
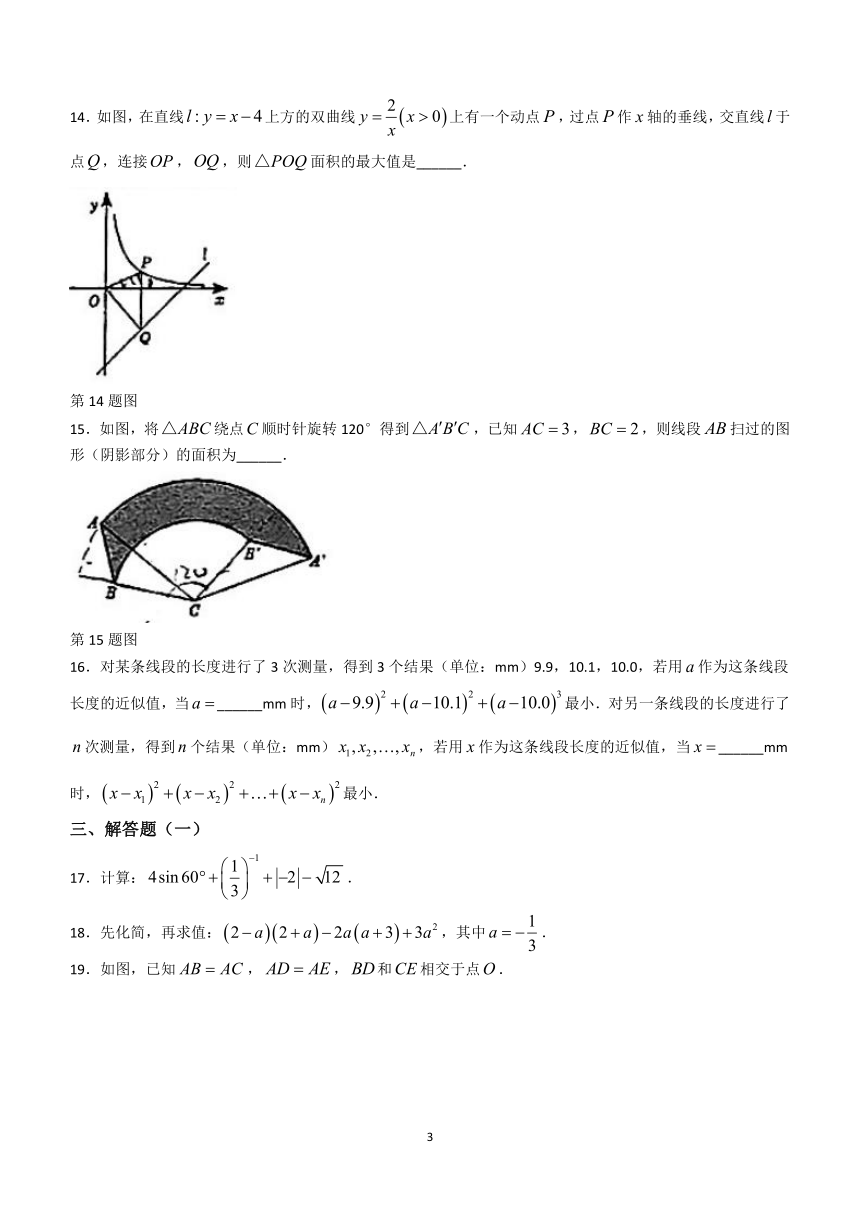
14.如图,在直线上方的双曲线上有一个动点,过点作轴的垂线,交直线于点,连接,,则面积的最大值是______.
第14题图
15.如图,将绕点顺时针旋转120°得到,已知,,则线段扫过的图形(阴影部分)的面积为______.
第15题图
16.对某条线段的长度进行了3次测量,得到3个结果(单位:mm)9.9,10.1,10.0,若用作为这条线段长度的近似值,当______mm时,最小.对另一条线段的长度进行了次测量,得到个结果(单位:mm),若用作为这条线段长度的近似值,当______mm时,最小.
三、解答题(一)
17.计算:.
18.先化简,再求值:,其中.
19.如图,已知,,和相交于点.
(1)求证:;
(2)判断的形状,并说明理由.
20.尺规作图.已知,点是上一点.
(1)过点作;
(2)在直线上求作一点,使点到,的距离相等;
(3)求证:.
四、解答题(二)
21.第19届亚运会,吉祥物为“宸宸”、“琼琼”、“莲莲”,今年学校准备举行“第19届亚运会”知识竞赛活动,拟购买30套吉祥物“宸宸”、“琼琼”、“莲莲”作为竞赛奖品.某商店有甲、乙两种规格,其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,且总费用不得超过2400元,试求一下该校一共有多少种购买方案?
22.如图,中,,是边上的一点,且,是上的一点,以为直径的经过点.
(1)求证:是的切线;
(2)若圆心到弦的距离为1,,求的长.
23.如图1,已知排球场的长度为18m,宽9m,位于球场中线处的球网的高度为2.24m.一球员定点发球技术非常稳定,当他站在底线中点处发球时,排球运动轨迹是如图2的抛物线,点为击球点,,球飞行到达最高点处时,其高度为2.6m,与的水平之距为6m,以为原点建立如图所示的平面直角坐标系(排球大小)忽略不计.
图1 图2
(1)当他站在底线中点处向正前方发球时,
①求排球飞行的高度与水平距离之间的函数关系式(不用写的取值范围).
②这次所发的球能够过网吗?如果能够过网,是否会出界?并说明理由.
(2)假设该球员改变发球方向和击球点高度时球运动轨迹的抛物线形状不变,在点处上方击球,要使球落在某一区域(以对方场地的边线底线交点为圆心,半径为1.5m的扇形)内,请直接写出击球点的高度范围______(,结果保留两位小数)
五、解答题(三)
24.【阅读理解】如图1,在矩形中,若,,由勾股定理,得,同理,故.
【探究发现】(1)如图2,四边形为平行四边形,,,则上述结论是否依然成立?请加以判断,并说明理由.
【拓展提升】(2)如图3,已知为的一条中线,,,.
求证:.
【尝试应用】(3)如图4,在矩形中,若,,点在边上,请求出的最小值.
图1 图2 图3 图4
25.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点.直线与抛物线交于,两点,与轴交于点,点的坐标为.
备用图
(1)请求出,两点的坐标及直线的函数表达式;
(2)若点是抛物线上的点,点的横坐标为,过点作轴,垂足为.与直线交于点,当点是线段的三等分点时,求点的坐标;
(3)若点是轴上的点,且,求点的坐标.
九年级数学期初大练习(B)
一、选择题
1.在实数,,,3.14中,无理数是( )
A. B. C. D.3.14
2.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3.在下列二次根式中,的取值范围是的是( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.不透明的盒子放有三张大小、形状及质地相同的卡片,卡片上分别写有李白《峨眉山月歌》,李白《渡荆门送别》和王维《寄荆州张丞相》三首诗,小明从盒子中随机抽取两张卡片,卡片上诗的作者都是李白的概率是( )
A. B. C. D.
6.不等式组的解集在数轴上表示为( )
A. B.
C. D.
7.若一个圆锥侧面展开图的圆心角是270°,圆锥母线与底面半径之间的函数关系图象大致是( )
A. B. C. D.
8.如图,在长方形中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A. B. C. D.
9.在下列函数图象上任取不同两点、,定能使成立的是( )
A. B.
C. D.
10.如左图,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点.设点运动的路程为,,右图是点运动时随变化的关系图象,则等边三角形的边长为( )
A.6 B.3 C. D.
二、填空题
11.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,该速度112000用科学记数法表示为______.
12.把多项式分解因式的结果是______.
13.已知一元二次方程的一个根为.则另一个根______.
14.如图,在直线上方的双曲线上有一个动点,过点作轴的垂线,交直线于点,连接,,则面积的最大值是______.
第14题图
15.如图,将绕点顺时针旋转120°得到,已知,,则线段扫过的图形(阴影部分)的面积为______.
第15题图
16.对某条线段的长度进行了3次测量,得到3个结果(单位:mm)9.9,10.1,10.0,若用作为这条线段长度的近似值,当______mm时,最小.对另一条线段的长度进行了次测量,得到个结果(单位:mm),若用作为这条线段长度的近似值,当______mm时,最小.
三、解答题(一)
17.计算:.
18.先化简,再求值:,其中.
19.如图,已知,,和相交于点.
(1)求证:;
(2)判断的形状,并说明理由.
20.尺规作图.已知,点是上一点.
(1)过点作;
(2)在直线上求作一点,使点到,的距离相等;
(3)求证:.
四、解答题(二)
21.第19届亚运会,吉祥物为“宸宸”、“琼琼”、“莲莲”,今年学校准备举行“第19届亚运会”知识竞赛活动,拟购买30套吉祥物“宸宸”、“琼琼”、“莲莲”作为竞赛奖品.某商店有甲、乙两种规格,其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,且总费用不得超过2400元,试求一下该校一共有多少种购买方案?
22.如图,中,,是边上的一点,且,是上的一点,以为直径的经过点.
(1)求证:是的切线;
(2)若圆心到弦的距离为1,,求的长.
23.如图1,已知排球场的长度为18m,宽9m,位于球场中线处的球网的高度为2.24m.一球员定点发球技术非常稳定,当他站在底线中点处发球时,排球运动轨迹是如图2的抛物线,点为击球点,,球飞行到达最高点处时,其高度为2.6m,与的水平之距为6m,以为原点建立如图所示的平面直角坐标系(排球大小)忽略不计.
图1 图2
(1)当他站在底线中点处向正前方发球时,
①求排球飞行的高度与水平距离之间的函数关系式(不用写的取值范围).
②这次所发的球能够过网吗?如果能够过网,是否会出界?并说明理由.
(2)假设该球员改变发球方向和击球点高度时球运动轨迹的抛物线形状不变,在点处上方击球,要使球落在某一区域(以对方场地的边线底线交点为圆心,半径为1.5m的扇形)内,请直接写出击球点的高度范围______(,结果保留两位小数)
五、解答题(三)
24.【阅读理解】如图1,在矩形中,若,,由勾股定理,得,同理,故.
【探究发现】(1)如图2,四边形为平行四边形,,,则上述结论是否依然成立?请加以判断,并说明理由.
【拓展提升】(2)如图3,已知为的一条中线,,,.
求证:.
【尝试应用】(3)如图4,在矩形中,若,,点在边上,请求出的最小值.
图1 图2 图3 图4
25.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点.直线与抛物线交于,两点,与轴交于点,点的坐标为.
备用图
(1)请求出,两点的坐标及直线的函数表达式;
(2)若点是抛物线上的点,点的横坐标为,过点作轴,垂足为.与直线交于点,当点是线段的三等分点时,求点的坐标;
(3)若点是轴上的点,且,求点的坐标.
同课章节目录
