2024年广东省深圳市中考数学高频易错题精选练习(二)(含解析)
文档属性
| 名称 | 2024年广东省深圳市中考数学高频易错题精选练习(二)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:01:41 | ||
图片预览



文档简介
2024年广东省深圳市中考数学高频易错题精选练习(二)
一、单选题
1.若规定向东走1m 记为1m ,则8m 表示( )
A.向东走8m B.向西走8m C.向西走8m D.向北走8m
2.下列图形既是中心对称又是轴对称图形的是( )
A. B. C. D.
3.十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107 B.1.46×107 C.1.46×109 D.1.46×1010
4.在九年级体育中考中,某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):46,44,45,42,48,46,47,46.则这组数据的中位数为( )
A.42 B.45 C.46 D.48
5.爬坡时坡角与水平面夹角为,则每爬1m耗能,若某人爬了1000m,该坡角为30°,则他耗能(参考数据:,)( )
A.58J B.159J C.1025J D.1732J
6.如图,在平行四边形中,两内角的平分线交于点,,,则的长是( )
A. B. C. D.
7.如图,两条直线相交于点O,若射线OC平分平角∠AOB,∠1=56°,则∠2等于( )
A.44° B.56° C.45° D.34°
8.某中学为准备“十四岁青春仪式”,原计划由八(1)班的个小组制作面彩旗,后因个小组另有任务,其余个小组的每名学生要比原计划多做面彩旗才能完成任务,如果这个小组的人数相等,设每个小组有学生名,根据题意可列方程得( )
A. B. C. D.
9.已知正方形轨道的边长为小明站在正方形轨道边的中点处,操控一辆无人驾驶小汽车,小汽车沿着折线以每秒的速度向点(终点)移动,如果将小汽车到小明的距离设为将小汽车运动的时间设为那么与之间关系的图象大致是( )
A. B.
C. D.
10.下列计算正确的是( )
A. B.
C. D.
二、填空题
11.一个口袋中装有4个红球,3个绿球,2个黄球,每个球除颜色外其他都相同,搅匀后随机的从中摸出一个球是绿球的概率是
12.已知a2+2a=1,则代数式2a2+4a+2的值为 .
13.如图,、是上的两点,是直径,若,则 .
14.如图,在平面直角坐标系中,点,点,点,连接,过点作双曲线交线段于点(不与点、重合),已知.
(1) .
(2)若,则的取值范围是 .
15.如图,在中,,,平分交于点,于点,有下列说法:①;②;③;④若的面积为1,点是边上的中点,则的面积为,其中正确的是 .
三、解答题
16.先化简,再求值:,其中,满足.
17.计算
(1)
(2)
18.“当你背单词时,阿拉斯加的鳕鱼正跃出水面;当你算数学时,南太平洋的海鸥正掠过海岸;当你晚自习时,地球的极圈正五彩斑斓;但少年,梦要你亲自实现,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现.”这是直播带货新平台“东方甄选”带货王董宇辉在推销鳕鱼时的台词.所推销鳕鱼的成本为每袋元,当售价为每袋元时,每分钟可销售袋. 为了吸引更多顾客,“东方甄选”采取降价措施.据市场调查反映:销售单价每降元,则每分钟可多销售袋.
(1)每袋鳕鱼的售价为多少元时,每分钟的销量为袋?
(2)“东方甄选”不忘公益初心,热心教育事业,其决定从每分钟利润中捐出元帮助留守儿童,为了保证捐款后每分钟利润达到元,且要最大限度让利消费者,求此时鳕鱼的销售单价为多少元?
19.如图,在中,,,点在边上,经过点和点且与边相交于点.
(1)判断与⊙D的位置关系,并说明理由;
(2)若,求⊙D的半径.
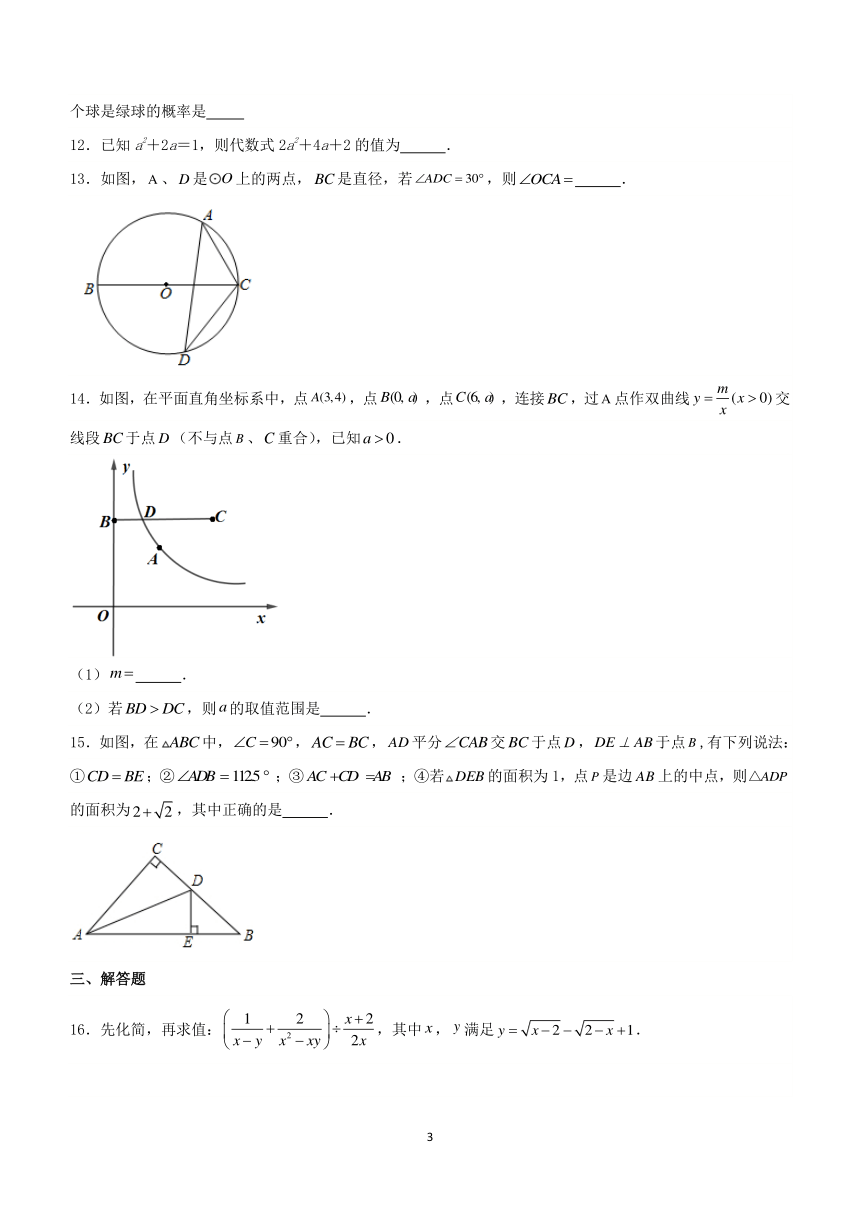
20.抛物线与x轴交于,B两点,与y轴交于点.
(1)求抛物线的解析式;
(2)①直接写出外接圆的圆心坐标;
②如图1,点E在第一象限抛物线上,连接,交于点D,连接,面积为4,求E点坐标.
(3)如图2,将直线绕点顺时针旋转后,得到的对应直线与抛物线有唯一公共点,求m与n的数量关系.
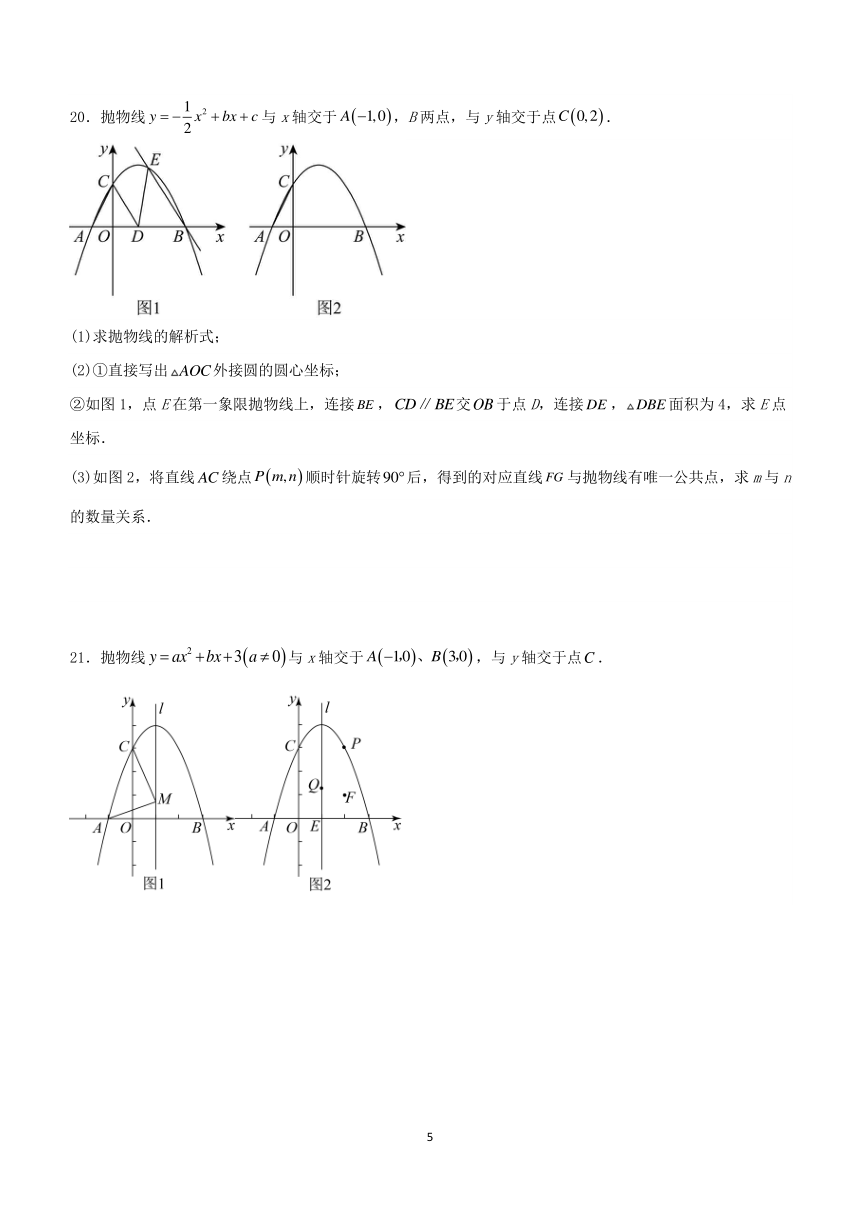
21.抛物线与x轴交于,与y轴交于点.
(1)求抛物线的表达式;
(2)如图1,M为抛物线对称轴l上一动点,连接,求的最小值及此时M点的坐标;
(3)如图2,抛物线的对称轴l与x轴交于点E,点,P为抛物线上一动点,Q为抛物线对称轴l上一动点,以点E、F、P、Q为顶点的四边形为平行四边形时,直接写出所有可能的点Q的坐标.
22.某学校九年级共400名男生,为了解实心球训练情况,从中随机抽取20名学生的实心球成绩作为样本,数据统计如下(单位:米):
9.6;5;8.6;8.3;9.5;10.3;7.2;6;5.4;7.7;7.6;5.1;12.5;5.5;7.4;7.3;8.1;10.2;9.3;4.8
根据数据绘制了如下的表格和统计图:
换算为体考分数 成绩(米) 频数
10 4
8 a
6 7
4 b
合计 20
根据上面提供的信息,回答下列问题:
(1)统计表中的_______,________;
(2)请补全条形统计图;
(3)在扇形统计图中,“8分”对应的圆心角的度数是_________;
(4)根据抽样调查结果,请估计该校九年级学生实心球体考分数不低于8分的有多少人?
参考答案
1.B
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【详解】解:根据题意知表示向西走,
故选:B.
【点睛】本题考查正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
2.D
【详解】试题解析:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误.
B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选D.
考点:1.中心对称图形;2.轴对称图形.
3.C
【详解】1460000000=1.46×109.
故选C.
点睛:对于一个绝对值较大的数,用科学记数法写成 的形式,其中,n是比原整数位数少1的数.
4.C
【分析】根据中位数的定义,把8个数据从小到大的顺序依次排列后,求第4,第5位两数的平均数即为本组数据的中位数.
【详解】解:把数据由小到大排列为:42,44,45,46,46,46,47,48
∴中位数为.
故答案为:46.
【点睛】找中位数的时候一定要先排好大小顺序,再根据奇数个数和偶数个数来确定中位数.如果是奇数个,则正中间的数字即为中位数;如果是偶数个,则找中间两个数的平均数为中位数.先将数据按从小到大顺序排列是求中位数的关键.
5.B
【分析】根据特殊角三角函数值计算求解.
【详解】
故选:B.
【点睛】本题考查特殊角三角函数值,掌握特殊角三角函数值是解题的关键.
6.B
【分析】根据平行四边形的性质及角平分线的定义、三角形内角和定理可得,再利用勾股定理即可求得的长.
【详解】解:∵四边形是平行四边形,
∴,,
∵平分,平分,
∴,,
∴,
∴,
∴是直角三角形,
∵,,
∴.
故选:B.
【点睛】本题考查平行四边形的性质,勾股定理,角平分线的定义,三角形内角和定理,直角三角形的判定.判定是直角三角形是解题的关键.
7.D
【分析】直接利用平角的定义结合垂直的定义和对顶角的性质分析得出答案.
【详解】∵射线OC平分平角∠AOB,
∴∠AOC=∠COB=90°,
∵∠1=56°,
∴∠2=90°﹣56°=34°.
故选D.
【点睛】此题主要考查了对顶角以及邻补角,正确把握相关定义是解题关键.
8.B
【分析】设每个小组有学生名,根据题意“其余个小组的每名学生要比原计划多做面彩旗才能完成任务”列出分式方程,即可求解.
【详解】解:设每个小组有学生名,根据题意可列方程得,
故选:B.
【点睛】本题考查了列分式方程,根据题意列出方程是解题的关键.
9.D
【分析】求出小汽车在AB、BC上运动时,MQ的表达式即可求解.
【详解】解:设小汽车所在的点为点Q,
①当点Q在AB上运动时,AQ=t,
则MQ2=MA2+AQ2=1+t2,
即MQ2为开口向上的抛物线,则MQ为曲线,
②当点Q在BC上运动时,
同理可得:MQ2=22+(1-t+2)2=4+(3-t)2,
MQ为曲线;
故选:D.
【点睛】本题考查了动点图象问题,解题的关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.
10.C
【详解】解:A、3a+2a=5a,故A错误;
B、4x-3x=x,故B错误;
C、正确;
D、不是同类项,不能合并,故D错误.
故选C.
11.
【分析】本题主要考查了概率公式的应用,用绿球的个数除以球的总数即可求解.
【详解】∵绿球的个数为3,球的总数为,
∴随机地从中摸出一个球是绿球的概率是,
故答案为:.
12.4
【分析】代数式2a2+4a+2化成2(a2+2a)+2,然后把a2+2a=1代入求值即可.
【详解】解:原式=2(a2+2a)+2,
把a2+2a=1代入上式,
原式=2×1+2
=4,
故答案为:4.
【点睛】本题是对代数式运算的考查,熟练掌握整体代入知识是解决本题的关键.
13.60°/60度
【分析】连接AB,如图,根据圆周角定理得到∠BAC=90°,∠B=∠ADC=30°,然后利用互余计算出∠ACB即可.
【详解】解:连接AB,如图,
∵BC是直径,
∴∠BAC=90°,
∵∠B=∠ADC=30°,
∴∠ACB=90°-∠B=90°-30°=60°,
即∠OCA=60°.
故答案为60°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
14. 12
【分析】(1)将点A坐标代入双曲线解析式即可求出m的值.
(2)由题意可用a表示出D点坐标.即可求出BD和DC的长.再由线段BC与双曲线有交点且与点B、C不重合和可列出不等式,解出不等式即可求出a的取值范围.
【详解】(1)由题意可知点A在双曲线上,
∴将点A坐标代入双曲线解析式得:,
解得:.
故答案为:12.
(2)由(1)可知该双曲线解析式为,
∵D点纵坐标为a,代入双曲线解析式得:,
即,
∴D点坐标为.
∵线段BC与双曲线有交点且与点B、C不重合,
∴,
解得:.
∵,,且.
∴.
∴.
综上可知.
故答案为:.
【点睛】本题考查利用待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征以及解不等式.利用数形结合的思想是解答本题的关键.
15.①②③
【分析】利用角平分线的性质和等腰直角三角形的性质可以证明①和②是正确的,证明,利用全等三角形的性质得到③是正确的,根据等腰直角三角形DEB的面积求出它的边长,再去算出大的等腰直角三角形ABC的边长,求出的面积证明④是错误的.
【详解】解:∵是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∵AD平分,,,
∴,
∴,故①正确;
∵AD平分,
∴,
∵,
∴在中,,故②正确;
在和中,
,
∴,
∴,
∵,
∴,故③正确;
∵是等腰直角三角形,且面积是1,
∴,,
∴,,
∵P是AB中点,
∴,
∴,故④错误.
故答案是:①②③.
【点睛】本题考查等腰直角三角形的性质,角平分线的性质和全等三角形的性质和判定,解题的关键是掌握这些性质定理结合题目条件进行证明求解.
16.,2
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,根据负数没有平方根求出与的值,代入计算即可求出值.
【详解】解:原式
,
,
∴,
即,
解得:,
原式.
【点睛】此题考查了分式的化简求值,以及二次根式有意义的条件,熟练掌握运算法则是解本题的关键.
17.(1)2;(2)
【分析】(1)根据实数的运算顺序计算即可;
(2)原式利用多项式除以单项式法则计算即可.
【详解】解:(1)
=
=2;
(2)
=
=
【点睛】此题考查了实数的混合运算,整式的除法,熟练掌握运算法则是解本题的关键.
18.(1)每袋鳕鱼的售价为元时,每分钟的销量为袋.
(2)鳕鱼的销售单价为元.
【分析】本题考查一元一次方程和一元二次方程的应用,解题的关键是根据题意,找到等量关系,列出方程,进行解答.
(1)设每袋鳕鱼的售价为元,根据题意,则,解出,即可;
(2)设此时鳕鱼的销售单价为元,根据题意,则方程为,解出方程,即可.
【详解】(1)解:设每袋鳕鱼的售价为元,每分钟的销售量为袋,
∴,
解得:,
答:每袋鳕鱼的售价为元时,每分钟的销售量为袋.
(2)解:设此时鳕鱼的销售单价为元,
∴,
解得:,,
∵要最大限度让利消费者,
∴,
答:此时鳕鱼的销售单价为元.
19.(1)AC是⊙D的切线,理由见解析;(2)⊙D的半径为6.
【分析】(1)连接AD,根据等腰三角形的性质得到∠B=∠C=30°,∠BAD=∠B=30°,求得∠ADC=60°,根据三角形的内角和得到∠DAC=180°-60°-30°=90°,于是得到AC是⊙D的切线;
(2)连接AE,推出△ADE是等边三角形,得到AE=DE,∠AED=60°,求得∠EAC=∠AED-∠C=30°,得到AE=CE=6,于是得到结论.
【详解】(1)证明:连接AD,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=60°,
∴∠DAC=180°-60°-30°=90°,
∵点A在⊙D上,
∴AC是⊙D的切线;
(2)解:连接AE,
∵AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=DE,∠AED=60°,
∴∠EAC=∠AED-∠C=30°,
∴∠EAC=∠C,
∴AE=CE=6,
∴⊙D的半径AD=6.
.
【点睛】本题考查了切线的判定和性质,等腰三角形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.
20.(1)
(2)①,②
(3)
【分析】(1)根据图象经过,,利用待定系数法求出解析式即可;
(2)①由是直角三角形得到外接圆的圆心是线段的中点,即可得到答案;②连接,,,,则,设点E的坐标为,利用列方程,求出,即可得到点E的坐标;
(3)过P作且,作轴,交x轴于N,过F作于M,连接,证明,则,得到F点坐标为,设旋转后得,则,则,,得到G点坐标为,求出直线的解析式为,由联立直线的解析式和二次函数解析式得,由直线与抛物线有唯一公共点,则,整理后即可得到答案.
【详解】(1)解:将,代入得,
,
解得,
∴抛物线的解析式为;
(2)①∵,
∴是直角三角形,
∴外接圆的圆心是线段的中点,
∵,,
∴外接圆的圆心坐标为,即;
②连接,,如图:
∵,,
∴,
设点E的坐标为,
令,即,
解得,,
∴点B的坐标为;
∴,
∵,
∴,
解得,
当时,,
∴点E的坐标为;
(3)如图,过P作且,作轴,交x轴于N,过F作于M,连接,
,
,
∵,,
∴,,
∴,
∴F点坐标为,
∵设旋转后得,则,
∴,,
∴G点坐标为,
设直线的解析式为,
则,
解得,
∴直线的解析式为,
∴由
得,
∵直线与抛物线有唯一公共点,
∴,
整理得.
即m与n的数量关系为.
【点睛】本题考查了二次函数的面积问题,待定系数法求二次函数解析式,求二次函数与坐标轴交点问题,旋转的性质,直角三角形外接圆,一元二次方程根的判别式,全等三角形的判定和性质,作出正确的辅助线,掌握二次函数的图像与性质是解题的关键.
21.(1)
(2),
(3),,
【分析】(1)待定系数法求解即可;
(2)如图1,连接,交于,连接,由题意知,抛物线的对称轴为直线,,可知当三点共线时,,此时值最小,在中,由勾股定理得,求的值,进而可得的最小值;设直线的解析式为,待定系数法求解,然后将代入求解值,进而可得的点坐标;
(3)设,以点E、F、P、Q为顶点的四边形为平行四边形时,分①为平行四边形的边;②为平行四边形的对角线两种情况求解,然后根据平行四边形对边平行且相等,对角线互相平分等性质进行求解即可.
【详解】(1)解:将代入得,,
解得,,
∴抛物线的表达式为;
(2)解:如图1,连接,交于,连接,
由题意知,抛物线的对称轴为直线,,
∴当三点共线时,,此时值最小,
当时,,
∴,
在中,由勾股定理得,
∴值最小为;
设直线的解析式为,
将,代入得,,
解得,,
∴直线的解析式为,
当时,,
∴,
∴的最小值为,;
(3)解:设,以点E、F、P、Q为顶点的四边形为平行四边形时,分两种情况求解:
①为平行四边形的边;
如图2,四边形为平行四边形,
∴,,
∴,,
∴;
如图3,四边形为平行四边形,
∴的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
②为平行四边形的对角线;
如图4,四边形为平行四边形,
的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
综上所述,以点E、F、P、Q为顶点的四边形为平行四边形时,所有可能的点Q的坐标为,,.
【点睛】本题考查了二次函数解析式,二次函数的图象与性质,二次函数与平行四边形综合,平行四边形的性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.
22.(1)6,3;(2)补全条形统计图见解析;(3);(4)该校九年级学生实心球体考分数不低于8分的有200人.
【分析】(1)结合数据统计即可;
(2)根据(1)中的结果,补全条形统计图即可;
(3)“8分”对应的圆心角的度数等于360°乘以它所对应的百分比;
(4)用400乘以不低于8分所占的百分比即可.
【详解】解:(1)由样本可知,符合7.7≤x≤9.5的有8.6,8.3,9.5,7.7,8.1,9.3共有6个,
∴a=6,
符合3.0≤x≤5.2的有5,5.1,4.8共3个,
∴b=3,
故答案为:6,3;
(2)补全条形统计图如图:
(3)∵,
∴“8分”对应的圆心角的度数是,
故答案为:;
(4)∵(人)
∴该校九年级学生实心球体考分数不低于8分的有200人.
【点睛】本题考查条形统计图和扇形统计图,用样本估计总体等.理解统计图表中的数量关系是正确计算的前提.
一、单选题
1.若规定向东走1m 记为1m ,则8m 表示( )
A.向东走8m B.向西走8m C.向西走8m D.向北走8m
2.下列图形既是中心对称又是轴对称图形的是( )
A. B. C. D.
3.十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107 B.1.46×107 C.1.46×109 D.1.46×1010
4.在九年级体育中考中,某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):46,44,45,42,48,46,47,46.则这组数据的中位数为( )
A.42 B.45 C.46 D.48
5.爬坡时坡角与水平面夹角为,则每爬1m耗能,若某人爬了1000m,该坡角为30°,则他耗能(参考数据:,)( )
A.58J B.159J C.1025J D.1732J
6.如图,在平行四边形中,两内角的平分线交于点,,,则的长是( )
A. B. C. D.
7.如图,两条直线相交于点O,若射线OC平分平角∠AOB,∠1=56°,则∠2等于( )
A.44° B.56° C.45° D.34°
8.某中学为准备“十四岁青春仪式”,原计划由八(1)班的个小组制作面彩旗,后因个小组另有任务,其余个小组的每名学生要比原计划多做面彩旗才能完成任务,如果这个小组的人数相等,设每个小组有学生名,根据题意可列方程得( )
A. B. C. D.
9.已知正方形轨道的边长为小明站在正方形轨道边的中点处,操控一辆无人驾驶小汽车,小汽车沿着折线以每秒的速度向点(终点)移动,如果将小汽车到小明的距离设为将小汽车运动的时间设为那么与之间关系的图象大致是( )
A. B.
C. D.
10.下列计算正确的是( )
A. B.
C. D.
二、填空题
11.一个口袋中装有4个红球,3个绿球,2个黄球,每个球除颜色外其他都相同,搅匀后随机的从中摸出一个球是绿球的概率是
12.已知a2+2a=1,则代数式2a2+4a+2的值为 .
13.如图,、是上的两点,是直径,若,则 .
14.如图,在平面直角坐标系中,点,点,点,连接,过点作双曲线交线段于点(不与点、重合),已知.
(1) .
(2)若,则的取值范围是 .
15.如图,在中,,,平分交于点,于点,有下列说法:①;②;③;④若的面积为1,点是边上的中点,则的面积为,其中正确的是 .
三、解答题
16.先化简,再求值:,其中,满足.
17.计算
(1)
(2)
18.“当你背单词时,阿拉斯加的鳕鱼正跃出水面;当你算数学时,南太平洋的海鸥正掠过海岸;当你晚自习时,地球的极圈正五彩斑斓;但少年,梦要你亲自实现,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现.”这是直播带货新平台“东方甄选”带货王董宇辉在推销鳕鱼时的台词.所推销鳕鱼的成本为每袋元,当售价为每袋元时,每分钟可销售袋. 为了吸引更多顾客,“东方甄选”采取降价措施.据市场调查反映:销售单价每降元,则每分钟可多销售袋.
(1)每袋鳕鱼的售价为多少元时,每分钟的销量为袋?
(2)“东方甄选”不忘公益初心,热心教育事业,其决定从每分钟利润中捐出元帮助留守儿童,为了保证捐款后每分钟利润达到元,且要最大限度让利消费者,求此时鳕鱼的销售单价为多少元?
19.如图,在中,,,点在边上,经过点和点且与边相交于点.
(1)判断与⊙D的位置关系,并说明理由;
(2)若,求⊙D的半径.
20.抛物线与x轴交于,B两点,与y轴交于点.
(1)求抛物线的解析式;
(2)①直接写出外接圆的圆心坐标;
②如图1,点E在第一象限抛物线上,连接,交于点D,连接,面积为4,求E点坐标.
(3)如图2,将直线绕点顺时针旋转后,得到的对应直线与抛物线有唯一公共点,求m与n的数量关系.
21.抛物线与x轴交于,与y轴交于点.
(1)求抛物线的表达式;
(2)如图1,M为抛物线对称轴l上一动点,连接,求的最小值及此时M点的坐标;
(3)如图2,抛物线的对称轴l与x轴交于点E,点,P为抛物线上一动点,Q为抛物线对称轴l上一动点,以点E、F、P、Q为顶点的四边形为平行四边形时,直接写出所有可能的点Q的坐标.
22.某学校九年级共400名男生,为了解实心球训练情况,从中随机抽取20名学生的实心球成绩作为样本,数据统计如下(单位:米):
9.6;5;8.6;8.3;9.5;10.3;7.2;6;5.4;7.7;7.6;5.1;12.5;5.5;7.4;7.3;8.1;10.2;9.3;4.8
根据数据绘制了如下的表格和统计图:
换算为体考分数 成绩(米) 频数
10 4
8 a
6 7
4 b
合计 20
根据上面提供的信息,回答下列问题:
(1)统计表中的_______,________;
(2)请补全条形统计图;
(3)在扇形统计图中,“8分”对应的圆心角的度数是_________;
(4)根据抽样调查结果,请估计该校九年级学生实心球体考分数不低于8分的有多少人?
参考答案
1.B
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【详解】解:根据题意知表示向西走,
故选:B.
【点睛】本题考查正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
2.D
【详解】试题解析:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误.
B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选D.
考点:1.中心对称图形;2.轴对称图形.
3.C
【详解】1460000000=1.46×109.
故选C.
点睛:对于一个绝对值较大的数,用科学记数法写成 的形式,其中,n是比原整数位数少1的数.
4.C
【分析】根据中位数的定义,把8个数据从小到大的顺序依次排列后,求第4,第5位两数的平均数即为本组数据的中位数.
【详解】解:把数据由小到大排列为:42,44,45,46,46,46,47,48
∴中位数为.
故答案为:46.
【点睛】找中位数的时候一定要先排好大小顺序,再根据奇数个数和偶数个数来确定中位数.如果是奇数个,则正中间的数字即为中位数;如果是偶数个,则找中间两个数的平均数为中位数.先将数据按从小到大顺序排列是求中位数的关键.
5.B
【分析】根据特殊角三角函数值计算求解.
【详解】
故选:B.
【点睛】本题考查特殊角三角函数值,掌握特殊角三角函数值是解题的关键.
6.B
【分析】根据平行四边形的性质及角平分线的定义、三角形内角和定理可得,再利用勾股定理即可求得的长.
【详解】解:∵四边形是平行四边形,
∴,,
∵平分,平分,
∴,,
∴,
∴,
∴是直角三角形,
∵,,
∴.
故选:B.
【点睛】本题考查平行四边形的性质,勾股定理,角平分线的定义,三角形内角和定理,直角三角形的判定.判定是直角三角形是解题的关键.
7.D
【分析】直接利用平角的定义结合垂直的定义和对顶角的性质分析得出答案.
【详解】∵射线OC平分平角∠AOB,
∴∠AOC=∠COB=90°,
∵∠1=56°,
∴∠2=90°﹣56°=34°.
故选D.
【点睛】此题主要考查了对顶角以及邻补角,正确把握相关定义是解题关键.
8.B
【分析】设每个小组有学生名,根据题意“其余个小组的每名学生要比原计划多做面彩旗才能完成任务”列出分式方程,即可求解.
【详解】解:设每个小组有学生名,根据题意可列方程得,
故选:B.
【点睛】本题考查了列分式方程,根据题意列出方程是解题的关键.
9.D
【分析】求出小汽车在AB、BC上运动时,MQ的表达式即可求解.
【详解】解:设小汽车所在的点为点Q,
①当点Q在AB上运动时,AQ=t,
则MQ2=MA2+AQ2=1+t2,
即MQ2为开口向上的抛物线,则MQ为曲线,
②当点Q在BC上运动时,
同理可得:MQ2=22+(1-t+2)2=4+(3-t)2,
MQ为曲线;
故选:D.
【点睛】本题考查了动点图象问题,解题的关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.
10.C
【详解】解:A、3a+2a=5a,故A错误;
B、4x-3x=x,故B错误;
C、正确;
D、不是同类项,不能合并,故D错误.
故选C.
11.
【分析】本题主要考查了概率公式的应用,用绿球的个数除以球的总数即可求解.
【详解】∵绿球的个数为3,球的总数为,
∴随机地从中摸出一个球是绿球的概率是,
故答案为:.
12.4
【分析】代数式2a2+4a+2化成2(a2+2a)+2,然后把a2+2a=1代入求值即可.
【详解】解:原式=2(a2+2a)+2,
把a2+2a=1代入上式,
原式=2×1+2
=4,
故答案为:4.
【点睛】本题是对代数式运算的考查,熟练掌握整体代入知识是解决本题的关键.
13.60°/60度
【分析】连接AB,如图,根据圆周角定理得到∠BAC=90°,∠B=∠ADC=30°,然后利用互余计算出∠ACB即可.
【详解】解:连接AB,如图,
∵BC是直径,
∴∠BAC=90°,
∵∠B=∠ADC=30°,
∴∠ACB=90°-∠B=90°-30°=60°,
即∠OCA=60°.
故答案为60°.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
14. 12
【分析】(1)将点A坐标代入双曲线解析式即可求出m的值.
(2)由题意可用a表示出D点坐标.即可求出BD和DC的长.再由线段BC与双曲线有交点且与点B、C不重合和可列出不等式,解出不等式即可求出a的取值范围.
【详解】(1)由题意可知点A在双曲线上,
∴将点A坐标代入双曲线解析式得:,
解得:.
故答案为:12.
(2)由(1)可知该双曲线解析式为,
∵D点纵坐标为a,代入双曲线解析式得:,
即,
∴D点坐标为.
∵线段BC与双曲线有交点且与点B、C不重合,
∴,
解得:.
∵,,且.
∴.
∴.
综上可知.
故答案为:.
【点睛】本题考查利用待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征以及解不等式.利用数形结合的思想是解答本题的关键.
15.①②③
【分析】利用角平分线的性质和等腰直角三角形的性质可以证明①和②是正确的,证明,利用全等三角形的性质得到③是正确的,根据等腰直角三角形DEB的面积求出它的边长,再去算出大的等腰直角三角形ABC的边长,求出的面积证明④是错误的.
【详解】解:∵是等腰直角三角形,
∴,
∵,
∴,
∴是等腰直角三角形,
∴,
∵AD平分,,,
∴,
∴,故①正确;
∵AD平分,
∴,
∵,
∴在中,,故②正确;
在和中,
,
∴,
∴,
∵,
∴,故③正确;
∵是等腰直角三角形,且面积是1,
∴,,
∴,,
∵P是AB中点,
∴,
∴,故④错误.
故答案是:①②③.
【点睛】本题考查等腰直角三角形的性质,角平分线的性质和全等三角形的性质和判定,解题的关键是掌握这些性质定理结合题目条件进行证明求解.
16.,2
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,根据负数没有平方根求出与的值,代入计算即可求出值.
【详解】解:原式
,
,
∴,
即,
解得:,
原式.
【点睛】此题考查了分式的化简求值,以及二次根式有意义的条件,熟练掌握运算法则是解本题的关键.
17.(1)2;(2)
【分析】(1)根据实数的运算顺序计算即可;
(2)原式利用多项式除以单项式法则计算即可.
【详解】解:(1)
=
=2;
(2)
=
=
【点睛】此题考查了实数的混合运算,整式的除法,熟练掌握运算法则是解本题的关键.
18.(1)每袋鳕鱼的售价为元时,每分钟的销量为袋.
(2)鳕鱼的销售单价为元.
【分析】本题考查一元一次方程和一元二次方程的应用,解题的关键是根据题意,找到等量关系,列出方程,进行解答.
(1)设每袋鳕鱼的售价为元,根据题意,则,解出,即可;
(2)设此时鳕鱼的销售单价为元,根据题意,则方程为,解出方程,即可.
【详解】(1)解:设每袋鳕鱼的售价为元,每分钟的销售量为袋,
∴,
解得:,
答:每袋鳕鱼的售价为元时,每分钟的销售量为袋.
(2)解:设此时鳕鱼的销售单价为元,
∴,
解得:,,
∵要最大限度让利消费者,
∴,
答:此时鳕鱼的销售单价为元.
19.(1)AC是⊙D的切线,理由见解析;(2)⊙D的半径为6.
【分析】(1)连接AD,根据等腰三角形的性质得到∠B=∠C=30°,∠BAD=∠B=30°,求得∠ADC=60°,根据三角形的内角和得到∠DAC=180°-60°-30°=90°,于是得到AC是⊙D的切线;
(2)连接AE,推出△ADE是等边三角形,得到AE=DE,∠AED=60°,求得∠EAC=∠AED-∠C=30°,得到AE=CE=6,于是得到结论.
【详解】(1)证明:连接AD,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=60°,
∴∠DAC=180°-60°-30°=90°,
∵点A在⊙D上,
∴AC是⊙D的切线;
(2)解:连接AE,
∵AD=DE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=DE,∠AED=60°,
∴∠EAC=∠AED-∠C=30°,
∴∠EAC=∠C,
∴AE=CE=6,
∴⊙D的半径AD=6.
.
【点睛】本题考查了切线的判定和性质,等腰三角形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.
20.(1)
(2)①,②
(3)
【分析】(1)根据图象经过,,利用待定系数法求出解析式即可;
(2)①由是直角三角形得到外接圆的圆心是线段的中点,即可得到答案;②连接,,,,则,设点E的坐标为,利用列方程,求出,即可得到点E的坐标;
(3)过P作且,作轴,交x轴于N,过F作于M,连接,证明,则,得到F点坐标为,设旋转后得,则,则,,得到G点坐标为,求出直线的解析式为,由联立直线的解析式和二次函数解析式得,由直线与抛物线有唯一公共点,则,整理后即可得到答案.
【详解】(1)解:将,代入得,
,
解得,
∴抛物线的解析式为;
(2)①∵,
∴是直角三角形,
∴外接圆的圆心是线段的中点,
∵,,
∴外接圆的圆心坐标为,即;
②连接,,如图:
∵,,
∴,
设点E的坐标为,
令,即,
解得,,
∴点B的坐标为;
∴,
∵,
∴,
解得,
当时,,
∴点E的坐标为;
(3)如图,过P作且,作轴,交x轴于N,过F作于M,连接,
,
,
∵,,
∴,,
∴,
∴F点坐标为,
∵设旋转后得,则,
∴,,
∴G点坐标为,
设直线的解析式为,
则,
解得,
∴直线的解析式为,
∴由
得,
∵直线与抛物线有唯一公共点,
∴,
整理得.
即m与n的数量关系为.
【点睛】本题考查了二次函数的面积问题,待定系数法求二次函数解析式,求二次函数与坐标轴交点问题,旋转的性质,直角三角形外接圆,一元二次方程根的判别式,全等三角形的判定和性质,作出正确的辅助线,掌握二次函数的图像与性质是解题的关键.
21.(1)
(2),
(3),,
【分析】(1)待定系数法求解即可;
(2)如图1,连接,交于,连接,由题意知,抛物线的对称轴为直线,,可知当三点共线时,,此时值最小,在中,由勾股定理得,求的值,进而可得的最小值;设直线的解析式为,待定系数法求解,然后将代入求解值,进而可得的点坐标;
(3)设,以点E、F、P、Q为顶点的四边形为平行四边形时,分①为平行四边形的边;②为平行四边形的对角线两种情况求解,然后根据平行四边形对边平行且相等,对角线互相平分等性质进行求解即可.
【详解】(1)解:将代入得,,
解得,,
∴抛物线的表达式为;
(2)解:如图1,连接,交于,连接,
由题意知,抛物线的对称轴为直线,,
∴当三点共线时,,此时值最小,
当时,,
∴,
在中,由勾股定理得,
∴值最小为;
设直线的解析式为,
将,代入得,,
解得,,
∴直线的解析式为,
当时,,
∴,
∴的最小值为,;
(3)解:设,以点E、F、P、Q为顶点的四边形为平行四边形时,分两种情况求解:
①为平行四边形的边;
如图2,四边形为平行四边形,
∴,,
∴,,
∴;
如图3,四边形为平行四边形,
∴的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
②为平行四边形的对角线;
如图4,四边形为平行四边形,
的中点坐标为,则,
当时,,则,
∴,
解得,,
∴;
综上所述,以点E、F、P、Q为顶点的四边形为平行四边形时,所有可能的点Q的坐标为,,.
【点睛】本题考查了二次函数解析式,二次函数的图象与性质,二次函数与平行四边形综合,平行四边形的性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.
22.(1)6,3;(2)补全条形统计图见解析;(3);(4)该校九年级学生实心球体考分数不低于8分的有200人.
【分析】(1)结合数据统计即可;
(2)根据(1)中的结果,补全条形统计图即可;
(3)“8分”对应的圆心角的度数等于360°乘以它所对应的百分比;
(4)用400乘以不低于8分所占的百分比即可.
【详解】解:(1)由样本可知,符合7.7≤x≤9.5的有8.6,8.3,9.5,7.7,8.1,9.3共有6个,
∴a=6,
符合3.0≤x≤5.2的有5,5.1,4.8共3个,
∴b=3,
故答案为:6,3;
(2)补全条形统计图如图:
(3)∵,
∴“8分”对应的圆心角的度数是,
故答案为:;
(4)∵(人)
∴该校九年级学生实心球体考分数不低于8分的有200人.
【点睛】本题考查条形统计图和扇形统计图,用样本估计总体等.理解统计图表中的数量关系是正确计算的前提.
同课章节目录
