2024年山东省济南市中考数学高频易错题精选练习(一)(含解析)
文档属性
| 名称 | 2024年山东省济南市中考数学高频易错题精选练习(一)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:25:58 | ||
图片预览

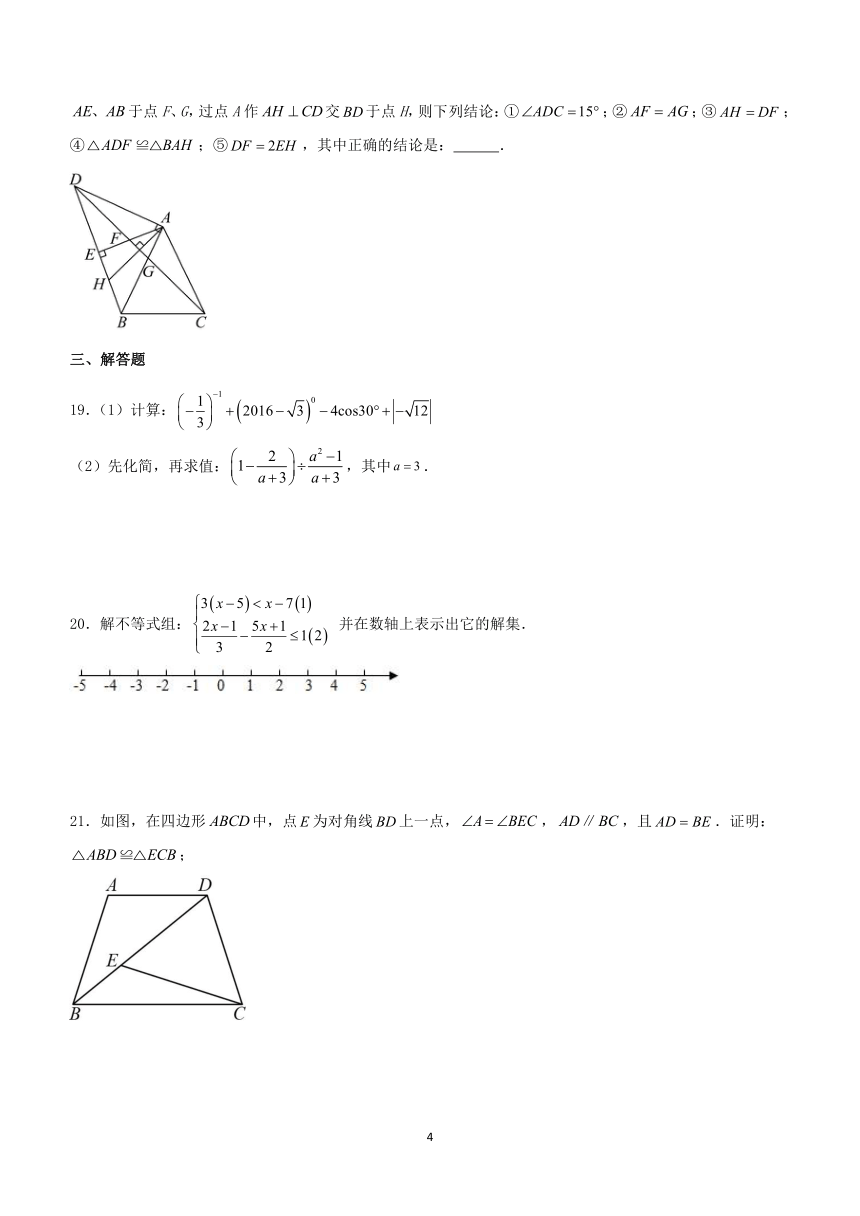
文档简介
2024年山东省济南市中考数学高频易错题精选练习(一)
一、单选题
1.下列各式中,正确的是( )
A. B. C. D.
2.如图所示的几何体的主视图是( )
A. B. C. D.
3.中国的陆地面积约为9600000km2,将数字9600000用科学记数法表示为a×10n,其中n的值为( )
A.6 B.7 C.8 D.9
4.从1,2,3,4,5这五个数中任选两个数,其和为偶数的概率为( )
A. B. C. D.
5.化简的结果是( )
A. B. C. D.
6.如图,为测量一根与地面垂直的旗杆的高度,在距离旗杆底端10米的处测得旗杆顶端的仰角,则旗杆的高度为( )
A.米 B.米 C.米 D.米
7.下面图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
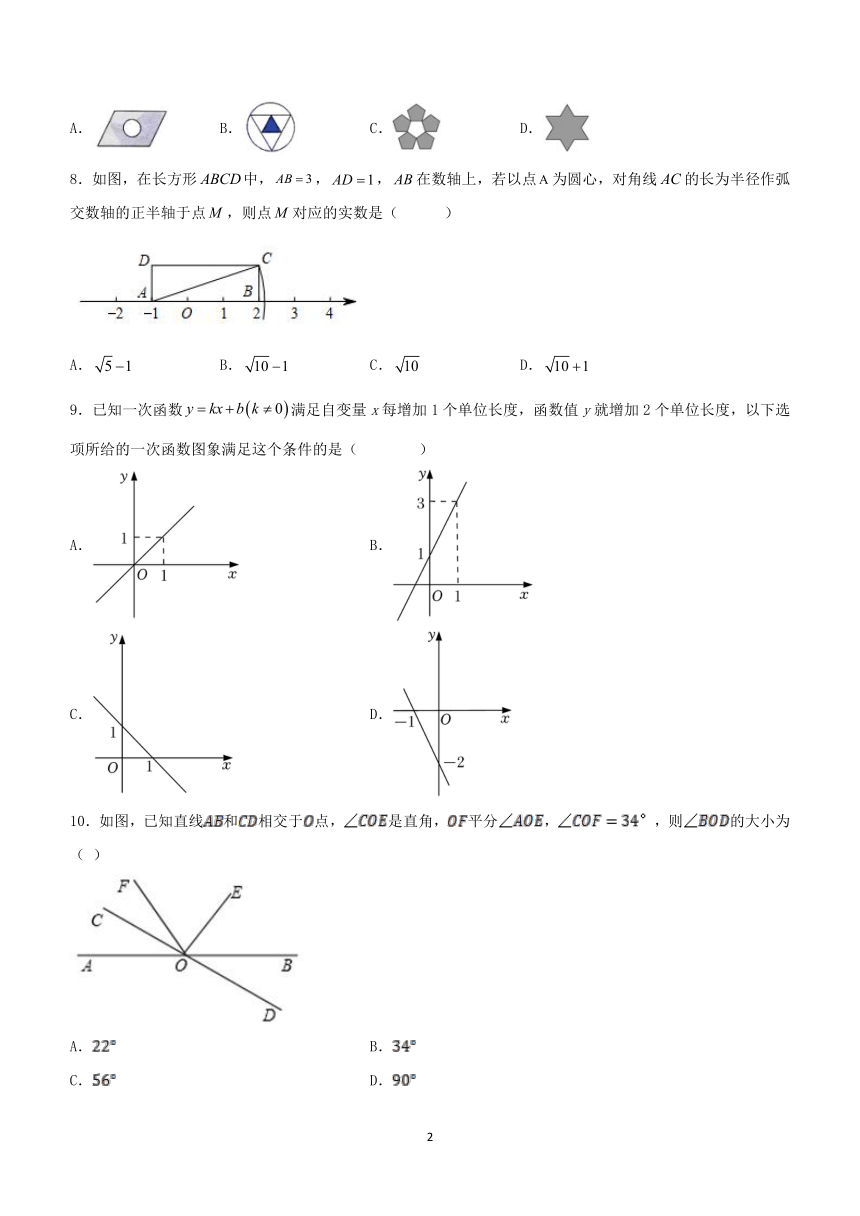
8.如图,在长方形中,,,在数轴上,若以点为圆心,对角线的长为半径作弧交数轴的正半轴于点,则点对应的实数是( )
A. B. C. D.
9.已知一次函数满足自变量x每增加1个单位长度,函数值y就增加2个单位长度,以下选项所给的一次函数图象满足这个条件的是( )
A. B.
C. D.
10.如图,已知直线和相交于点,是直角,平分,,则的大小为( )
A. B.
C. D.
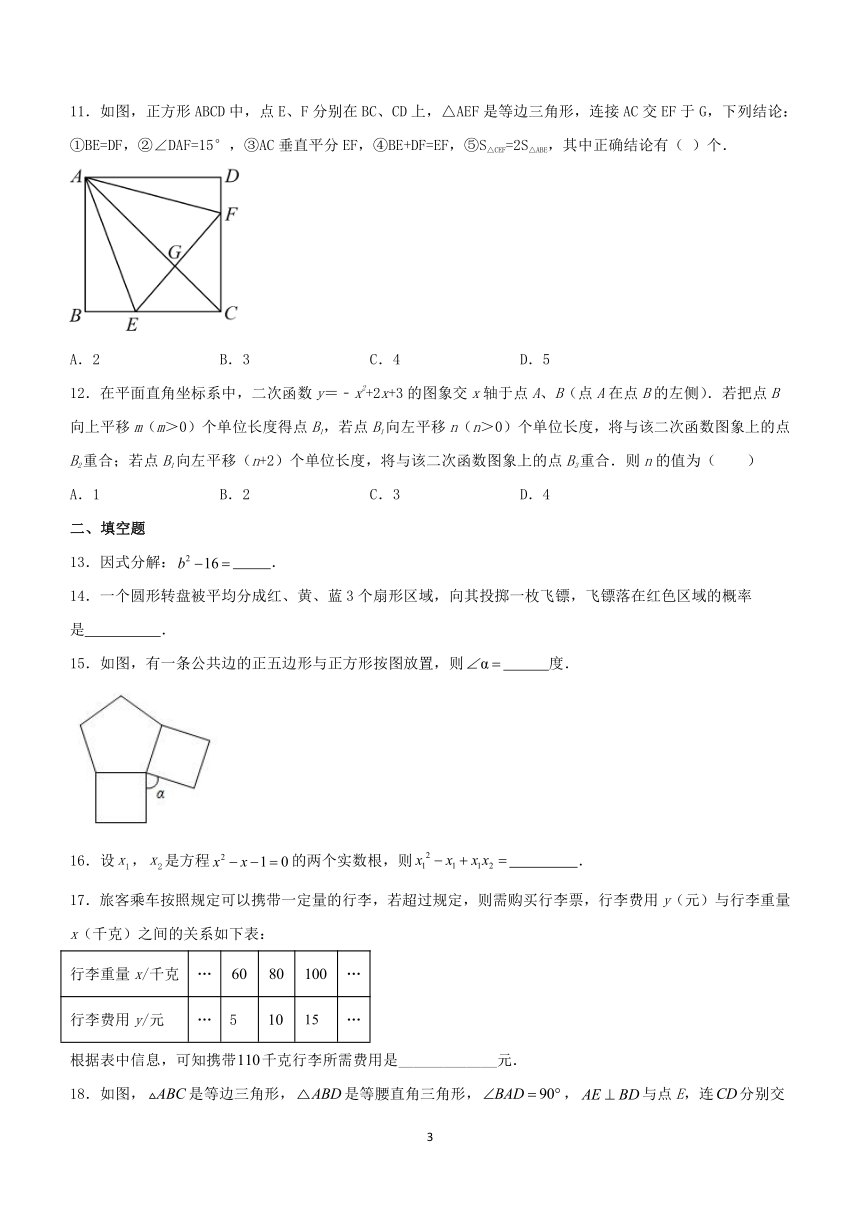
11.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE,其中正确结论有( )个.
A.2 B.3 C.4 D.5
12.在平面直角坐标系中,二次函数y=﹣x2+2x+3的图象交x轴于点A、B(点A在点B的左侧).若把点B向上平移m(m>0)个单位长度得点B1,若点B1向左平移n(n>0)个单位长度,将与该二次函数图象上的点B2重合;若点B1向左平移(n+2)个单位长度,将与该二次函数图象上的点B3重合.则n的值为( )
A.1 B.2 C.3 D.4
二、填空题
13.因式分解: .
14.一个圆形转盘被平均分成红、黄、蓝3个扇形区域,向其投掷一枚飞镖,飞镖落在红色区域的概率是 .
15.如图,有一条公共边的正五边形与正方形按图放置,则 度.
16.设,是方程的两个实数根,则 .
17.旅客乘车按照规定可以携带一定量的行李,若超过规定,则需购买行李票,行李费用y(元)与行李重量x(千克)之间的关系如下表:
行李重量x/千克 … …
行李费用y/元 … 5 …
根据表中信息,可知携带千克行李所需费用是_____________元.
18.如图,是等边三角形,是等腰直角三角形,,与点E,连分别交于点F、G,过点A作交于点H,则下列结论:①;②;③;④;⑤,其中正确的结论是: .
三、解答题
19.(1)计算:
(2)先化简,再求值:,其中.
20.解不等式组: 并在数轴上表示出它的解集.
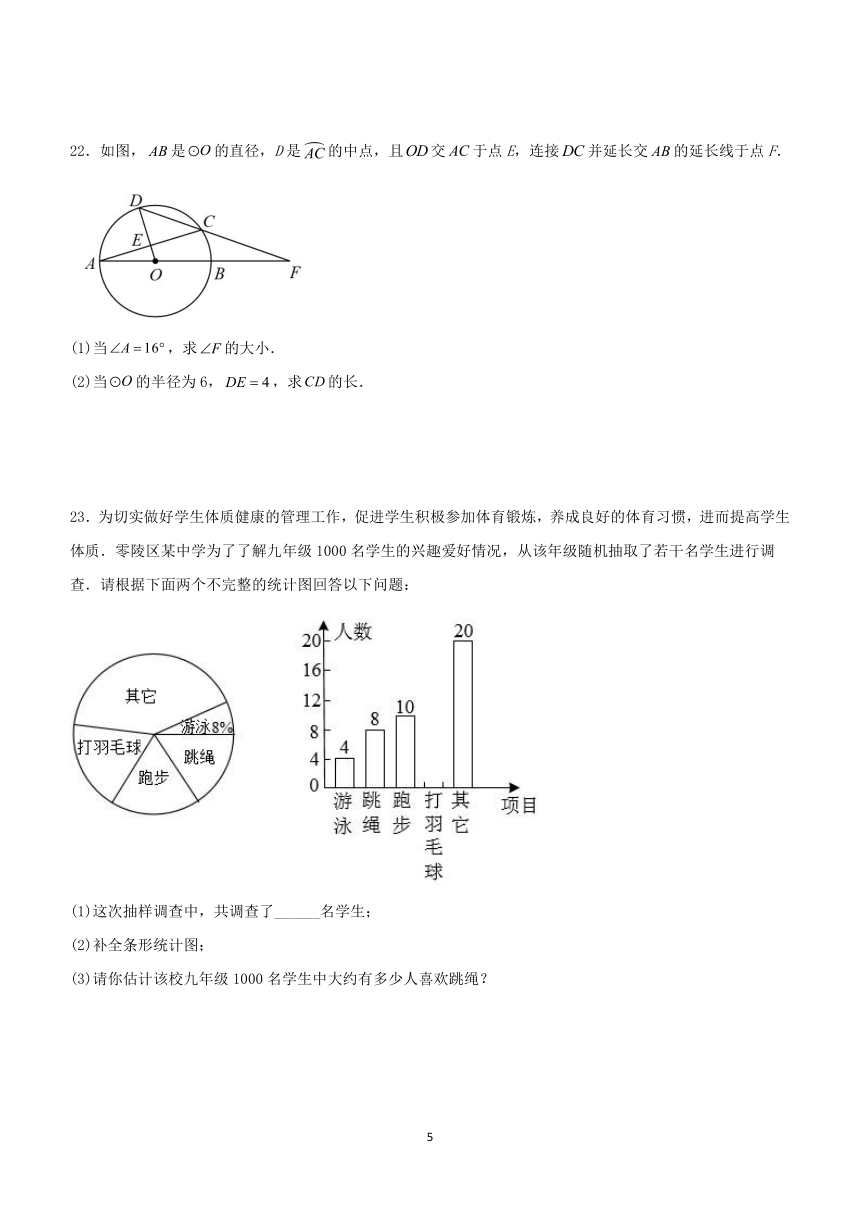
21.如图,在四边形中,点为对角线上一点,,,且.证明:;
22.如图,是的直径,D是的中点,且交于点E,连接并延长交的延长线于点F.
(1)当,求的大小.
(2)当的半径为6,,求的长.
23.为切实做好学生体质健康的管理工作,促进学生积极参加体育锻炼,养成良好的体育习惯,进而提高学生体质.零陵区某中学为了了解九年级1000名学生的兴趣爱好情况,从该年级随机抽取了若干名学生进行调查.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了______名学生;
(2)补全条形统计图;
(3)请你估计该校九年级1000名学生中大约有多少人喜欢跳绳?
24.为了做好新冠疫情的防控工作,某超市计划购进A,B两种消毒液出售,A种消毒液比B种消毒液每瓶进价少3元,已知用1600元购进的A种消毒液的数量是1100元购进的B种消毒液数量的2倍.
(1)求A,B两种消毒液每瓶进价各是多少元?
(2)疫情进入了防控常态,该超市老板决定用不超过1960元购进A、B两种消毒液共200瓶,已知A种消毒液售价为14元,B种消毒液售价为18元,请设计出该超市售完该批消毒液后获得最大利润的购进方案,并求出最大利润.
25.如图,一次函数的图象与轴交于点A,正方形ABCD的顶点B在轴上,点D在直线上,且AO=OB,反比例函数()经过点C.
(1)求一次函数和反比例函数的解析式;
(2)点P是轴上一动点,当的周长最小时,求出P点的坐标;
(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.
26.【操作】如图①,在矩形中,为对角线上一点(不与点重合),将沿射线方向平移到的位置,的对应点为.已知(不需要证明).
【探究】过图①中的点作交延长线于点,连接,其它条件不变,如图②.求证:.
【拓展】将图②中的沿翻折得到,连接,其它条件不变,如图③.当最短时,若,,直接写出的长和此时四边形的周长.
27.如图1,已知抛物线与x轴相交于两点,并与直线交于两点,其中点C是直线与y轴的交点,连接.
(1)点B的坐标是 ;点C的坐标是 ;
(2)求抛物线的解析式;
(3)设点E是线段上的一个动点(不与点B、C重合),直线轴,交抛物线与点F,问点E运动到何处时,线段的长最大?并求出的长的最大值;
(4)如图2,点D是抛物线的顶点,判断直线是否是经过A、B、C三点的圆的切线,并说明理由.
参考答案
1.D
【详解】A、=2,故本选项错误;
B、=3,故本选项错误;
C、=9,故本选项错误;
D、=13,故本选项正确.
故选D.
2.B
【分析】根据从正面看得到的图形是主视图,可得答案.
【详解】解:从正面看到的图形如下:
故选:B.
【点睛】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
3.A
【分析】根据科学记数法的定义进行判断可得正确答案.
【详解】解:9600000=,
n的值为6.
所以A选项是正确的.
【点睛】本题主要考查科学记数法表示较大的数时,其一般形式为,(其中1≤|a|<10,n为整数).
4.B
【分析】根据列表法求概率即可求解.
【详解】解:列表如下,
1 2 3 4 5
1 3 4 5 6
2 3 5 6 7
3 4 5 7 8
4 5 6 7 9
5 6 7 8 9
共有20种等可能结果,其中和为偶数的有8种,
则其和为偶数的概率为
故选B
【点睛】本题考查了列表法求概率,掌握求概率的方法是解题的关键.
5.A
【分析】直接将括号里面通分,进而分解因式,再利用分式的除法运算法则计算得出答案.
【详解】解:
=
=
=.
故选:A.
【点睛】此题主要考查了分式的混合运算,熟练掌握运算法则是解题关键.
6.D
【分析】根据题意得:BH=10米,,然后再在中,利用正切函数,即可求得旗杆的高度.
【详解】解:∵,,
∴为直角三角形,
∴,
∴,
又∵BH=10米,
∴米,
故选:D.
【点睛】本题主要考查了解直角三角形的应用,要根据所求和已知的条件正确的选用合适的三角形函数进行求解,难度一般.
7.D
【分析】平面内一个图形绕着某个点旋转后,如果与初始图形重合,那么这个图形叫做中心对称图形;一个图形沿着某一条直线折叠,如果直线两旁的部分重合,那么这个图形叫做轴对称图形;根据这两个概念对四个选项进行一一判断即可得出答案.
【详解】解:A、是中心对称图形但不是轴对称图形,故该选项不符合题意;
B、是轴对称图形但不是中心对称图形,故该选项不符合题意;
C、是轴对称图形但不是中心对称图形,故该选项不符合题意;
D、既是中心对称图形又是轴对称图形,故该选项符合题意;
故选:D.
【点睛】此题考查了中心对称图形与轴对称图形,熟练掌握中心对称图形与轴对称图形的概念是解答此题的关键.
8.B
【分析】在中根据勾股定理求出的长度,进而得到的长度,再根据点表示的数为,可得点表示的数.
【详解】在长方形中,,,
,,
在中,由勾股定理得:
,
以点为圆心,对角线的长为半径作弧交数轴的正半轴于点,
,
点表示的数为:.
故选:B.
【点睛】本题考查了勾股定理的应用以及如何在数轴上表示一个无理数,会用勾股定理是解题的关键.
9.B
【分析】根据题意和一次函数的性质,可以判断哪个选项中的图象符合题意.
【详解】解:∵一次函数y=kx+b(k≠0)满足自变量x每增加1个单位长度,函数值y就增加2个单位长度,
∴y随x的增大而增大,排除C、D,
A选项,自变量x每增加1个单位长度,函数值y就增加1个单位长度,不符合题意,
B选项,自变量x每增加1个单位长度,函数值y就增加2个单位长度,符合题意,
故选:B.
【点睛】本题考查一次函数的性质、一次函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
10.A
【详解】因为是直角,所以
又因为平分,所以
因为所以所以.
11.C
【详解】解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,∴AE=EF=AF,∠EAF=60°.∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,AE =AF,AB=AD,∴Rt△ABE≌Rt△ADF(HL).
∴BE=DF.故结论①正确.
由Rt△ABE≌Rt△ADF得,∠BAE=∠DAF,
∴∠DAF+∠DAF=30°.即∠DAF=15°.故结论②正确.
∵BC=CD,∴BC-BE=CD-DF,CE=CF.
∵AE=AF,∴AC垂直平分EF.故结论③正确.
设EC=x,由勾股定理,得EF=,CG=,AG=,
∴AC=.∴AB=.∴BE=.
∴BE+DF.故结论④错误.
∵,,
∴.故结论⑤正确.
综上所述,正确的有4个,
故选:C.
12.A
【分析】根据题意写出B2,B3的坐标,再由对称轴方程列出n的方程,求得n即可得到答案.
【详解】解:(1)y=0,则﹣x2+2x+3=0,解得,x1=3,x2=﹣1,
∴B(3,0),
由题意得,B1(3,m),B2(3﹣n,m),B3(1﹣n,m),
函数图象的对称轴为直线x==1,
∵点B2,B3在二次函数图象上且纵坐标相同,
∴=1,
∴n=1,
故选:A.
【点睛】本题主要考查了二次函数的图象与性质,求函数与坐标轴的交点坐标,平移的性质,表示出B1(3,m),B2(3-n,m),B3(1-n,m)是解题的关键.
13.
【分析】直接利用平方差公式进行分解即可.
【详解】解:,
故答案为:.
【点睛】此题主要考查了平方差公式分解因式,关键是熟练掌握平方差公式.
14..
【详解】试题分析:根据面积法:指针指向红色区域的概率就是红色区域的面积与总面积的比即可解答.
∵圆形转盘均分成红、黄、绿3个扇形区域,其中红色区域占1份,
∴指针落在红色区域的概率是.
故答案为
考点:几何概率.
15.72
【分析】先求出正五边形和正方形的一个内角的度数,再求出答案即可.
【详解】解:正五边形的一个内角的度数是,正方形的一个内角的度数是,
所以,
故答案为:.
【点睛】本题考查了正多边形内角问题,能求出正五边形的一个内角的度数是解此题的关键.
16.0
【分析】利用方程根的定义得到x12 x1=1,利用一元二次方程根与系数的关系得到x1x2=-1,然后整体代入进行计算.
【详解】解:∵x1,x2是方程x2 x 1=0的两个实数根,
∴x12 x1=1,x1x2=-1,
则x12 x1+x1x2=1-1=0,
故答案为0.
【点睛】本题考查一元二次方程根的定义和根与系数的关系,整体思想的应用是解决问题的关键.
17.
【分析】从图中信息得知,行李费用y(元)与行李重量x(千克)之间的关系满足一次函数关系,设出关系式,根据图中信息即可求出关系式,再将代入即可知道携带千克行李所需费用.
【详解】解:设行李费用y(元)与行李重量x(千克)的一次函数关系式:,
把和代入,得
解得,所以
把代入,得
故答案为:.
【点睛】本题主要考查得是一次函数的应用,通过图上信息确定函数类型是解题的关键.
18.①③④⑤
【分析】①由等边三角形与等腰直角三角形知是等腰三角形且顶角,据此可判断; ②求出和度数,从而得出∠AGF度数,据此可判断; ③根据证明即可判断③④正确; 由, , 则即可判断⑤.
【详解】解:∵为等边三角形,为等腰直角三角形,
∴、 、,
∴是等腰三角形,且顶角,
∴,故①正确;
∵, 即,
∴,
∴,,
∴,由知,故②错误;
记与的交点为,
由且,
,
则,
在和中,
∴,
∴,故③④正确;
∵,,,
∴,
∴,
∴,故⑤正确;
正确的为①③④⑤,
故答案为:①③④⑤.
【点睛】本题考查全等三角形的判定与性质,等腰三角形的性质和判定,等边三角形的性质,直角三角形的性质,解题的关键是掌握等腰三角形的性质、全等三角形的判定与性质.
19.(1);(2),
【分析】(1)分别利用负整数指数幂和零指数幂及特殊的三角函数值计算即可;
(2)首先将括号内的式子进行通分,然后再将除法统一为乘法运算,进而约分、化简,再代值求解.
【详解】(1)
;
(2)
当时,
原式.
【点睛】本题考查了实数的混合运算,分式的化简求值,熟练掌握特殊角的三角函数值以及分式的运算法则是解答本题的关键.
20.-1≤x<4
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:解不等式(1),得:x<4,
解不等式(2),得:x≥-1,
∴不等式组的解集为-1≤x<4,
将不等式的解集表示在数轴上如下:
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
21.证明见解析
【分析】根据平行线的性质可得,然后根据直接证明得即可得结论.
【详解】证明:∵,
∴,
在与中,
,
;
【点睛】本题主要考查了平行线的判定及全等三角形的判定及性质,熟练运用全等三角形的判定及性质是解题的关键.
22.(1)
(2)
【分析】(1)先求出,再利用三角形外角的性质求解;
(2)先利用勾股定理求出,再利用勾股定理即可求出.
【详解】(1)解:如图,连接,
∵D是的中点,
∴,
∵半圆所对的圆周角是
∴,
∵
∴,
∴.
(2)∵D是的中点,
∴垂直平分,
如图,连接,
在中,,
∴在中,,
∴的长为.
【点睛】本题考查了垂径定理的推论、圆周角定理的推论、三角形外角的性质、勾股定理等内容,解题关键是牢记相关概念和计算公式.
23.(1);
(2)见解析;
(3)有160人喜欢跳绳
【分析】(1)根据扇形统计图与条形统计图中游泳人数所占的百分比求解即可;
(2)根据样本的容量结合条形统计图,即可求得打羽毛球的人数,进而补全条形统计图;
(3)根据1000乘以跳绳的人数所占样本的比例即可求得答案
【详解】(1)4÷8%=50(人)
故答案为:50
(2)游泳的人数为:(人)
如图,
(3)1000×=160(人)
答:该校九年级1000名学生中大约有160人喜欢跳绳
【点睛】本题考查了条形统计图与扇形统计图信息关联,样本估计总体,从统计图中获取信息是解题的关键.
24.(1)A种消毒液每瓶进价是8元,B种消毒液每瓶进价是11元
(2)购进A种消毒液80瓶,B种消毒液120瓶时获得最大利润,最大利润是1320元
【分析】(1)设A种消毒液x元,则B种消毒液(x+3)元,根据题意得,解得,即可得可得B种消毒液的价钱;
(2)设购进A种消毒液a瓶,B种消毒液(200-a)瓶,根据题意得,解得,设售完该批消毒液获得总利润为w元,则,根据二次函数的性质可得w随a的增大而减小,则当a=80时,w有最大值,即可得B种消毒液的瓶数,w的最大值为1320元.
【详解】(1)解:设A种消毒液每瓶进价x元,则B种消毒液每瓶进价(x+3)元,
∴B种消毒液的价钱为:(元),
则A种消毒液每瓶进价是8元,B种消毒液每瓶进价是11元.
(2)解:设购进A种消毒液a瓶,B种消毒液(200-a)瓶,
设售完该批消毒液获得总利润为w元,
∵,
∴w随a的增大而减小,
∴当a=80时,w有最大值,
则B种消毒液: (瓶),
w的最大值: (元),
则购进A种消毒液80瓶,B种消毒液120瓶时获得最大利润,最大利润是1320元.
【点睛】本题考查了分式方程的应用,一次函数的应用,解题的关键是理解题意,找出等量关系.
25.(1)y=x+2,;(2)P(,0);(3)M的坐标为(,2),(,6)或(,﹣2).
【分析】(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,利用一次函数图象上点的坐标特征、正方形的性质以及等腰三角形的性质可得出点E的坐标,由点E的坐标利用待定系数法可求出一次函数解析式,由BD∥OA,OE=OB可求出BD的长,进而可得出点D的坐标,由正方形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可求出反比例函数解析式;
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,由点D的坐标可得出点D'的坐标,由点C,D'的坐标,利用待定系数法可求出直线CD'的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)设点M的坐标为(x,y),分DP为对角线、CD为对角线及CP为对角线三种情况,利用平行四边形的性质(对角线互相平分)可求出点M的坐标,此题得解.
【详解】(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,如图1所示.
当x=0时,y=kx+2=2,∴OA=2.
∵四边形ABCD为正方形,OA=OB,∴∠BAE=90°,∠OAB=∠OBA=45°,∴∠OAE=∠OEA=45°,∴OE=OA=2,点E的坐标为(﹣2,0).
将E(﹣2,0)代入y=kx+2,得:﹣2k+2=0,解得:k=1,∴一次函数的解析式为y=x+2.
∵∠OBD=∠ABD+∠OBA=90°,∴BD∥OA.
∵OE=OB=2,∴BD=2OA=4,∴点D的坐标为(2,4).
∵四边形ABCD为正方形,∴点C的坐标为(2+2﹣0,0+4﹣2),即(4,2).
∵反比例函数y(x>0)经过点C,∴n=4×2=8,∴反比例函数解析式为y.
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,如图2所示.
∵点D的坐标为(2,4),∴点D'的坐标为(2,﹣4).
设直线CD'的解析式为y=ax+b(a≠0),将C(4,2),D'(2,﹣4)代入y=ax+b,得:,解得:,∴直线CD'的解析式为y=3x﹣10.
当y=0时,3x﹣10=0,解得:x,∴当△PCD的周长最小时,P点的坐标为(,0).
(3)设点M的坐标为(x,y),分三种情况考虑,如图3所示.
①当DP为对角线时,,解得:,∴点M1的坐标为(,2);
②当CD为对角线时,,解得:,∴点M2的坐标为(,6);
③当CP为对角线时,,解得:,∴点M3的坐标为(,﹣2).
综上所述:以点C、D、P为顶点作平行四边形,第四个顶点M的坐标为(,2),(,6)或(,﹣2).
【点睛】本题考查了待定系数法求一次函数解析式、反比例函数图象上点的坐标特征、正方形的性质、等腰三角形的性质、三角形中位线、反比例函数图象上点的坐标特征、一次函数图象上点的坐标特征以及平行四边形的性质,解题的关键是:(1)利用等腰三角形的性质及正方形的性质,求出点E,C的坐标;(2)利用两点之间线段最短,确定点P的位置;(3)分DP为对角线、CD为对角线及CP为对角线三种情况,利用平行四边形的对角线互相平分求出点M的坐标.
26.探究:见解析;拓展: 四边形的周长为
【分析】探究:证明四边形EGBC是平行四边形,推出EG=BC,利用SAS证明三角形全等即可.
拓展:如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.由题意四边形AGFC是平行四边形,推出GF=AC=,由BF=BF′,可以假设BF=x,则BG=利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′= 此时点F′与O重合,由此即可解决问题.
【详解】解:探究:由平移,
∴,即
又∵,∴四边形为平行四边形
∴
∵,∴∠CBF=∠ACB,
∵
∴∠AEG=∠ACB,
∴∠AEG=∠CBF
∴.
拓展:
如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.
∵四边形ABCD是矩形, ∴∠ABC=90°,AB=4,BC=2,
∴
∵
∴,
∴
由题意四边形AGFC是平行四边形, ∴GF=AC=,
∵BF=BF′,可以假设BF=x,则BG=
∵AC∥GF, ∴∠BOK=∠HBF′,
∵∠BKO=∠F′HB=90°,
∴△F′HB∽△BKO,
∴
∴
∴
∴
∵ >0,
∴当 时,GF′的值最小,
此时点F′与O重合,由对折得:
由矩形的性质得:
四边形BFCF′是菱形,
四边形BFCF′的周长为,
且与互相平分,
由勾股定理得:
【点睛】本题属于四边形综合题,考查了矩形的性质,翻折变换,平行四边形的判定和性质,相似三角形的判定和性质,二次函数的性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会构建二次函数解决最值问题,属于中考压轴题.
27.(1),(2);(3),的最大值为2;(4)直线是经过A、B、C三点的圆的切线,理由见解析.
【分析】(1)先令x=0,y=0,求出点C,B坐标,
(2)把点C,B坐标代入抛物线求出a,c的值即可,
(3)由点在直线上设出点E的坐标,表示出线段的长度,运用二次函数最大值的知识求出点E的位置,
(4)先判断出是经过A、B、C三点的圆的直径,确定圆心,连接圆心和切点,证明垂直即可.
【详解】解:(1)由题意知直线交x轴、y轴于点B、C两点,
,
故答答案为:
(2)经过点B,C,
∴,
解得,
∴;
(3)如图1:
设点,
∵直线轴,
∴点,
,
,
所以当时,有最大值是2,
此时,的最大值为2;
(4)如图2:
与x轴相交于两点,
令,得,
解得:,或,
,
,
,
,
,
,
,
是经过A、B、C三点的圆的直径,
设圆心Q,则,连接,过点D作轴,垂足为E,连接,
顶点坐标为,
可求,,,,,
计算得:,
,
∴直线是经过A、B、C三点的圆的切线.
【点睛】此题主要考查二次函数的综合问题,会求函数与坐标轴的交点,会用点的坐标表示线段长度,知道运用二次函数解决最值问题,熟悉圆的切线的证明是解题的关键.
一、单选题
1.下列各式中,正确的是( )
A. B. C. D.
2.如图所示的几何体的主视图是( )
A. B. C. D.
3.中国的陆地面积约为9600000km2,将数字9600000用科学记数法表示为a×10n,其中n的值为( )
A.6 B.7 C.8 D.9
4.从1,2,3,4,5这五个数中任选两个数,其和为偶数的概率为( )
A. B. C. D.
5.化简的结果是( )
A. B. C. D.
6.如图,为测量一根与地面垂直的旗杆的高度,在距离旗杆底端10米的处测得旗杆顶端的仰角,则旗杆的高度为( )
A.米 B.米 C.米 D.米
7.下面图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
8.如图,在长方形中,,,在数轴上,若以点为圆心,对角线的长为半径作弧交数轴的正半轴于点,则点对应的实数是( )
A. B. C. D.
9.已知一次函数满足自变量x每增加1个单位长度,函数值y就增加2个单位长度,以下选项所给的一次函数图象满足这个条件的是( )
A. B.
C. D.
10.如图,已知直线和相交于点,是直角,平分,,则的大小为( )
A. B.
C. D.
11.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE,其中正确结论有( )个.
A.2 B.3 C.4 D.5
12.在平面直角坐标系中,二次函数y=﹣x2+2x+3的图象交x轴于点A、B(点A在点B的左侧).若把点B向上平移m(m>0)个单位长度得点B1,若点B1向左平移n(n>0)个单位长度,将与该二次函数图象上的点B2重合;若点B1向左平移(n+2)个单位长度,将与该二次函数图象上的点B3重合.则n的值为( )
A.1 B.2 C.3 D.4
二、填空题
13.因式分解: .
14.一个圆形转盘被平均分成红、黄、蓝3个扇形区域,向其投掷一枚飞镖,飞镖落在红色区域的概率是 .
15.如图,有一条公共边的正五边形与正方形按图放置,则 度.
16.设,是方程的两个实数根,则 .
17.旅客乘车按照规定可以携带一定量的行李,若超过规定,则需购买行李票,行李费用y(元)与行李重量x(千克)之间的关系如下表:
行李重量x/千克 … …
行李费用y/元 … 5 …
根据表中信息,可知携带千克行李所需费用是_____________元.
18.如图,是等边三角形,是等腰直角三角形,,与点E,连分别交于点F、G,过点A作交于点H,则下列结论:①;②;③;④;⑤,其中正确的结论是: .
三、解答题
19.(1)计算:
(2)先化简,再求值:,其中.
20.解不等式组: 并在数轴上表示出它的解集.
21.如图,在四边形中,点为对角线上一点,,,且.证明:;
22.如图,是的直径,D是的中点,且交于点E,连接并延长交的延长线于点F.
(1)当,求的大小.
(2)当的半径为6,,求的长.
23.为切实做好学生体质健康的管理工作,促进学生积极参加体育锻炼,养成良好的体育习惯,进而提高学生体质.零陵区某中学为了了解九年级1000名学生的兴趣爱好情况,从该年级随机抽取了若干名学生进行调查.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了______名学生;
(2)补全条形统计图;
(3)请你估计该校九年级1000名学生中大约有多少人喜欢跳绳?
24.为了做好新冠疫情的防控工作,某超市计划购进A,B两种消毒液出售,A种消毒液比B种消毒液每瓶进价少3元,已知用1600元购进的A种消毒液的数量是1100元购进的B种消毒液数量的2倍.
(1)求A,B两种消毒液每瓶进价各是多少元?
(2)疫情进入了防控常态,该超市老板决定用不超过1960元购进A、B两种消毒液共200瓶,已知A种消毒液售价为14元,B种消毒液售价为18元,请设计出该超市售完该批消毒液后获得最大利润的购进方案,并求出最大利润.
25.如图,一次函数的图象与轴交于点A,正方形ABCD的顶点B在轴上,点D在直线上,且AO=OB,反比例函数()经过点C.
(1)求一次函数和反比例函数的解析式;
(2)点P是轴上一动点,当的周长最小时,求出P点的坐标;
(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.
26.【操作】如图①,在矩形中,为对角线上一点(不与点重合),将沿射线方向平移到的位置,的对应点为.已知(不需要证明).
【探究】过图①中的点作交延长线于点,连接,其它条件不变,如图②.求证:.
【拓展】将图②中的沿翻折得到,连接,其它条件不变,如图③.当最短时,若,,直接写出的长和此时四边形的周长.
27.如图1,已知抛物线与x轴相交于两点,并与直线交于两点,其中点C是直线与y轴的交点,连接.
(1)点B的坐标是 ;点C的坐标是 ;
(2)求抛物线的解析式;
(3)设点E是线段上的一个动点(不与点B、C重合),直线轴,交抛物线与点F,问点E运动到何处时,线段的长最大?并求出的长的最大值;
(4)如图2,点D是抛物线的顶点,判断直线是否是经过A、B、C三点的圆的切线,并说明理由.
参考答案
1.D
【详解】A、=2,故本选项错误;
B、=3,故本选项错误;
C、=9,故本选项错误;
D、=13,故本选项正确.
故选D.
2.B
【分析】根据从正面看得到的图形是主视图,可得答案.
【详解】解:从正面看到的图形如下:
故选:B.
【点睛】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
3.A
【分析】根据科学记数法的定义进行判断可得正确答案.
【详解】解:9600000=,
n的值为6.
所以A选项是正确的.
【点睛】本题主要考查科学记数法表示较大的数时,其一般形式为,(其中1≤|a|<10,n为整数).
4.B
【分析】根据列表法求概率即可求解.
【详解】解:列表如下,
1 2 3 4 5
1 3 4 5 6
2 3 5 6 7
3 4 5 7 8
4 5 6 7 9
5 6 7 8 9
共有20种等可能结果,其中和为偶数的有8种,
则其和为偶数的概率为
故选B
【点睛】本题考查了列表法求概率,掌握求概率的方法是解题的关键.
5.A
【分析】直接将括号里面通分,进而分解因式,再利用分式的除法运算法则计算得出答案.
【详解】解:
=
=
=.
故选:A.
【点睛】此题主要考查了分式的混合运算,熟练掌握运算法则是解题关键.
6.D
【分析】根据题意得:BH=10米,,然后再在中,利用正切函数,即可求得旗杆的高度.
【详解】解:∵,,
∴为直角三角形,
∴,
∴,
又∵BH=10米,
∴米,
故选:D.
【点睛】本题主要考查了解直角三角形的应用,要根据所求和已知的条件正确的选用合适的三角形函数进行求解,难度一般.
7.D
【分析】平面内一个图形绕着某个点旋转后,如果与初始图形重合,那么这个图形叫做中心对称图形;一个图形沿着某一条直线折叠,如果直线两旁的部分重合,那么这个图形叫做轴对称图形;根据这两个概念对四个选项进行一一判断即可得出答案.
【详解】解:A、是中心对称图形但不是轴对称图形,故该选项不符合题意;
B、是轴对称图形但不是中心对称图形,故该选项不符合题意;
C、是轴对称图形但不是中心对称图形,故该选项不符合题意;
D、既是中心对称图形又是轴对称图形,故该选项符合题意;
故选:D.
【点睛】此题考查了中心对称图形与轴对称图形,熟练掌握中心对称图形与轴对称图形的概念是解答此题的关键.
8.B
【分析】在中根据勾股定理求出的长度,进而得到的长度,再根据点表示的数为,可得点表示的数.
【详解】在长方形中,,,
,,
在中,由勾股定理得:
,
以点为圆心,对角线的长为半径作弧交数轴的正半轴于点,
,
点表示的数为:.
故选:B.
【点睛】本题考查了勾股定理的应用以及如何在数轴上表示一个无理数,会用勾股定理是解题的关键.
9.B
【分析】根据题意和一次函数的性质,可以判断哪个选项中的图象符合题意.
【详解】解:∵一次函数y=kx+b(k≠0)满足自变量x每增加1个单位长度,函数值y就增加2个单位长度,
∴y随x的增大而增大,排除C、D,
A选项,自变量x每增加1个单位长度,函数值y就增加1个单位长度,不符合题意,
B选项,自变量x每增加1个单位长度,函数值y就增加2个单位长度,符合题意,
故选:B.
【点睛】本题考查一次函数的性质、一次函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
10.A
【详解】因为是直角,所以
又因为平分,所以
因为所以所以.
11.C
【详解】解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,∴AE=EF=AF,∠EAF=60°.∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,AE =AF,AB=AD,∴Rt△ABE≌Rt△ADF(HL).
∴BE=DF.故结论①正确.
由Rt△ABE≌Rt△ADF得,∠BAE=∠DAF,
∴∠DAF+∠DAF=30°.即∠DAF=15°.故结论②正确.
∵BC=CD,∴BC-BE=CD-DF,CE=CF.
∵AE=AF,∴AC垂直平分EF.故结论③正确.
设EC=x,由勾股定理,得EF=,CG=,AG=,
∴AC=.∴AB=.∴BE=.
∴BE+DF.故结论④错误.
∵,,
∴.故结论⑤正确.
综上所述,正确的有4个,
故选:C.
12.A
【分析】根据题意写出B2,B3的坐标,再由对称轴方程列出n的方程,求得n即可得到答案.
【详解】解:(1)y=0,则﹣x2+2x+3=0,解得,x1=3,x2=﹣1,
∴B(3,0),
由题意得,B1(3,m),B2(3﹣n,m),B3(1﹣n,m),
函数图象的对称轴为直线x==1,
∵点B2,B3在二次函数图象上且纵坐标相同,
∴=1,
∴n=1,
故选:A.
【点睛】本题主要考查了二次函数的图象与性质,求函数与坐标轴的交点坐标,平移的性质,表示出B1(3,m),B2(3-n,m),B3(1-n,m)是解题的关键.
13.
【分析】直接利用平方差公式进行分解即可.
【详解】解:,
故答案为:.
【点睛】此题主要考查了平方差公式分解因式,关键是熟练掌握平方差公式.
14..
【详解】试题分析:根据面积法:指针指向红色区域的概率就是红色区域的面积与总面积的比即可解答.
∵圆形转盘均分成红、黄、绿3个扇形区域,其中红色区域占1份,
∴指针落在红色区域的概率是.
故答案为
考点:几何概率.
15.72
【分析】先求出正五边形和正方形的一个内角的度数,再求出答案即可.
【详解】解:正五边形的一个内角的度数是,正方形的一个内角的度数是,
所以,
故答案为:.
【点睛】本题考查了正多边形内角问题,能求出正五边形的一个内角的度数是解此题的关键.
16.0
【分析】利用方程根的定义得到x12 x1=1,利用一元二次方程根与系数的关系得到x1x2=-1,然后整体代入进行计算.
【详解】解:∵x1,x2是方程x2 x 1=0的两个实数根,
∴x12 x1=1,x1x2=-1,
则x12 x1+x1x2=1-1=0,
故答案为0.
【点睛】本题考查一元二次方程根的定义和根与系数的关系,整体思想的应用是解决问题的关键.
17.
【分析】从图中信息得知,行李费用y(元)与行李重量x(千克)之间的关系满足一次函数关系,设出关系式,根据图中信息即可求出关系式,再将代入即可知道携带千克行李所需费用.
【详解】解:设行李费用y(元)与行李重量x(千克)的一次函数关系式:,
把和代入,得
解得,所以
把代入,得
故答案为:.
【点睛】本题主要考查得是一次函数的应用,通过图上信息确定函数类型是解题的关键.
18.①③④⑤
【分析】①由等边三角形与等腰直角三角形知是等腰三角形且顶角,据此可判断; ②求出和度数,从而得出∠AGF度数,据此可判断; ③根据证明即可判断③④正确; 由, , 则即可判断⑤.
【详解】解:∵为等边三角形,为等腰直角三角形,
∴、 、,
∴是等腰三角形,且顶角,
∴,故①正确;
∵, 即,
∴,
∴,,
∴,由知,故②错误;
记与的交点为,
由且,
,
则,
在和中,
∴,
∴,故③④正确;
∵,,,
∴,
∴,
∴,故⑤正确;
正确的为①③④⑤,
故答案为:①③④⑤.
【点睛】本题考查全等三角形的判定与性质,等腰三角形的性质和判定,等边三角形的性质,直角三角形的性质,解题的关键是掌握等腰三角形的性质、全等三角形的判定与性质.
19.(1);(2),
【分析】(1)分别利用负整数指数幂和零指数幂及特殊的三角函数值计算即可;
(2)首先将括号内的式子进行通分,然后再将除法统一为乘法运算,进而约分、化简,再代值求解.
【详解】(1)
;
(2)
当时,
原式.
【点睛】本题考查了实数的混合运算,分式的化简求值,熟练掌握特殊角的三角函数值以及分式的运算法则是解答本题的关键.
20.-1≤x<4
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:解不等式(1),得:x<4,
解不等式(2),得:x≥-1,
∴不等式组的解集为-1≤x<4,
将不等式的解集表示在数轴上如下:
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
21.证明见解析
【分析】根据平行线的性质可得,然后根据直接证明得即可得结论.
【详解】证明:∵,
∴,
在与中,
,
;
【点睛】本题主要考查了平行线的判定及全等三角形的判定及性质,熟练运用全等三角形的判定及性质是解题的关键.
22.(1)
(2)
【分析】(1)先求出,再利用三角形外角的性质求解;
(2)先利用勾股定理求出,再利用勾股定理即可求出.
【详解】(1)解:如图,连接,
∵D是的中点,
∴,
∵半圆所对的圆周角是
∴,
∵
∴,
∴.
(2)∵D是的中点,
∴垂直平分,
如图,连接,
在中,,
∴在中,,
∴的长为.
【点睛】本题考查了垂径定理的推论、圆周角定理的推论、三角形外角的性质、勾股定理等内容,解题关键是牢记相关概念和计算公式.
23.(1);
(2)见解析;
(3)有160人喜欢跳绳
【分析】(1)根据扇形统计图与条形统计图中游泳人数所占的百分比求解即可;
(2)根据样本的容量结合条形统计图,即可求得打羽毛球的人数,进而补全条形统计图;
(3)根据1000乘以跳绳的人数所占样本的比例即可求得答案
【详解】(1)4÷8%=50(人)
故答案为:50
(2)游泳的人数为:(人)
如图,
(3)1000×=160(人)
答:该校九年级1000名学生中大约有160人喜欢跳绳
【点睛】本题考查了条形统计图与扇形统计图信息关联,样本估计总体,从统计图中获取信息是解题的关键.
24.(1)A种消毒液每瓶进价是8元,B种消毒液每瓶进价是11元
(2)购进A种消毒液80瓶,B种消毒液120瓶时获得最大利润,最大利润是1320元
【分析】(1)设A种消毒液x元,则B种消毒液(x+3)元,根据题意得,解得,即可得可得B种消毒液的价钱;
(2)设购进A种消毒液a瓶,B种消毒液(200-a)瓶,根据题意得,解得,设售完该批消毒液获得总利润为w元,则,根据二次函数的性质可得w随a的增大而减小,则当a=80时,w有最大值,即可得B种消毒液的瓶数,w的最大值为1320元.
【详解】(1)解:设A种消毒液每瓶进价x元,则B种消毒液每瓶进价(x+3)元,
∴B种消毒液的价钱为:(元),
则A种消毒液每瓶进价是8元,B种消毒液每瓶进价是11元.
(2)解:设购进A种消毒液a瓶,B种消毒液(200-a)瓶,
设售完该批消毒液获得总利润为w元,
∵,
∴w随a的增大而减小,
∴当a=80时,w有最大值,
则B种消毒液: (瓶),
w的最大值: (元),
则购进A种消毒液80瓶,B种消毒液120瓶时获得最大利润,最大利润是1320元.
【点睛】本题考查了分式方程的应用,一次函数的应用,解题的关键是理解题意,找出等量关系.
25.(1)y=x+2,;(2)P(,0);(3)M的坐标为(,2),(,6)或(,﹣2).
【分析】(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,利用一次函数图象上点的坐标特征、正方形的性质以及等腰三角形的性质可得出点E的坐标,由点E的坐标利用待定系数法可求出一次函数解析式,由BD∥OA,OE=OB可求出BD的长,进而可得出点D的坐标,由正方形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可求出反比例函数解析式;
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,由点D的坐标可得出点D'的坐标,由点C,D'的坐标,利用待定系数法可求出直线CD'的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)设点M的坐标为(x,y),分DP为对角线、CD为对角线及CP为对角线三种情况,利用平行四边形的性质(对角线互相平分)可求出点M的坐标,此题得解.
【详解】(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,如图1所示.
当x=0时,y=kx+2=2,∴OA=2.
∵四边形ABCD为正方形,OA=OB,∴∠BAE=90°,∠OAB=∠OBA=45°,∴∠OAE=∠OEA=45°,∴OE=OA=2,点E的坐标为(﹣2,0).
将E(﹣2,0)代入y=kx+2,得:﹣2k+2=0,解得:k=1,∴一次函数的解析式为y=x+2.
∵∠OBD=∠ABD+∠OBA=90°,∴BD∥OA.
∵OE=OB=2,∴BD=2OA=4,∴点D的坐标为(2,4).
∵四边形ABCD为正方形,∴点C的坐标为(2+2﹣0,0+4﹣2),即(4,2).
∵反比例函数y(x>0)经过点C,∴n=4×2=8,∴反比例函数解析式为y.
(2)作点D关于x轴的对称点D',连接CD'交x轴于点P,此时△PCD的周长取最小值,如图2所示.
∵点D的坐标为(2,4),∴点D'的坐标为(2,﹣4).
设直线CD'的解析式为y=ax+b(a≠0),将C(4,2),D'(2,﹣4)代入y=ax+b,得:,解得:,∴直线CD'的解析式为y=3x﹣10.
当y=0时,3x﹣10=0,解得:x,∴当△PCD的周长最小时,P点的坐标为(,0).
(3)设点M的坐标为(x,y),分三种情况考虑,如图3所示.
①当DP为对角线时,,解得:,∴点M1的坐标为(,2);
②当CD为对角线时,,解得:,∴点M2的坐标为(,6);
③当CP为对角线时,,解得:,∴点M3的坐标为(,﹣2).
综上所述:以点C、D、P为顶点作平行四边形,第四个顶点M的坐标为(,2),(,6)或(,﹣2).
【点睛】本题考查了待定系数法求一次函数解析式、反比例函数图象上点的坐标特征、正方形的性质、等腰三角形的性质、三角形中位线、反比例函数图象上点的坐标特征、一次函数图象上点的坐标特征以及平行四边形的性质,解题的关键是:(1)利用等腰三角形的性质及正方形的性质,求出点E,C的坐标;(2)利用两点之间线段最短,确定点P的位置;(3)分DP为对角线、CD为对角线及CP为对角线三种情况,利用平行四边形的对角线互相平分求出点M的坐标.
26.探究:见解析;拓展: 四边形的周长为
【分析】探究:证明四边形EGBC是平行四边形,推出EG=BC,利用SAS证明三角形全等即可.
拓展:如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.由题意四边形AGFC是平行四边形,推出GF=AC=,由BF=BF′,可以假设BF=x,则BG=利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′= 此时点F′与O重合,由此即可解决问题.
【详解】解:探究:由平移,
∴,即
又∵,∴四边形为平行四边形
∴
∵,∴∠CBF=∠ACB,
∵
∴∠AEG=∠ACB,
∴∠AEG=∠CBF
∴.
拓展:
如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.
∵四边形ABCD是矩形, ∴∠ABC=90°,AB=4,BC=2,
∴
∵
∴,
∴
由题意四边形AGFC是平行四边形, ∴GF=AC=,
∵BF=BF′,可以假设BF=x,则BG=
∵AC∥GF, ∴∠BOK=∠HBF′,
∵∠BKO=∠F′HB=90°,
∴△F′HB∽△BKO,
∴
∴
∴
∴
∵ >0,
∴当 时,GF′的值最小,
此时点F′与O重合,由对折得:
由矩形的性质得:
四边形BFCF′是菱形,
四边形BFCF′的周长为,
且与互相平分,
由勾股定理得:
【点睛】本题属于四边形综合题,考查了矩形的性质,翻折变换,平行四边形的判定和性质,相似三角形的判定和性质,二次函数的性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会构建二次函数解决最值问题,属于中考压轴题.
27.(1),(2);(3),的最大值为2;(4)直线是经过A、B、C三点的圆的切线,理由见解析.
【分析】(1)先令x=0,y=0,求出点C,B坐标,
(2)把点C,B坐标代入抛物线求出a,c的值即可,
(3)由点在直线上设出点E的坐标,表示出线段的长度,运用二次函数最大值的知识求出点E的位置,
(4)先判断出是经过A、B、C三点的圆的直径,确定圆心,连接圆心和切点,证明垂直即可.
【详解】解:(1)由题意知直线交x轴、y轴于点B、C两点,
,
故答答案为:
(2)经过点B,C,
∴,
解得,
∴;
(3)如图1:
设点,
∵直线轴,
∴点,
,
,
所以当时,有最大值是2,
此时,的最大值为2;
(4)如图2:
与x轴相交于两点,
令,得,
解得:,或,
,
,
,
,
,
,
,
是经过A、B、C三点的圆的直径,
设圆心Q,则,连接,过点D作轴,垂足为E,连接,
顶点坐标为,
可求,,,,,
计算得:,
,
∴直线是经过A、B、C三点的圆的切线.
【点睛】此题主要考查二次函数的综合问题,会求函数与坐标轴的交点,会用点的坐标表示线段长度,知道运用二次函数解决最值问题,熟悉圆的切线的证明是解题的关键.
同课章节目录
