2024年山东省济南市中考数学高频易错题精选练习(二)(含解析)
文档属性
| 名称 | 2024年山东省济南市中考数学高频易错题精选练习(二)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:29:30 | ||
图片预览



文档简介
2024年山东省济南市中考数学高频易错题精选练习(二)
一、单选题
1.下列函数(1)y=πx;(2)y=2x-1;(3) ;(4)y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
2.一个袋子中装有4个相同的小球,它们分别标有号码1,2,3,4,摇匀后随机取出一球,记下号码后放回:再将小球摇匀,并从袋中随机取出一球,则第二次取出的球的号码不大于第一次取出的球的号码的概率为( )
A. B. C. D.
3.一个水平放置的几何体的三视图如图所示,则这个几何体是( )
A.B.C.D.
4.改革开放之后,靠近上海的苏南地区凭借外向型产业快速发展,紧邻上海的苏州的工业经济也得以高速发展,吸引了大量人口进入,截止2019年3月苏州市常住人口为1075万人,1075用科学记数法表示为()
A. B. C. D.
5.如图,数轴上点、对应的数分别是1,2,过点作,以点为圆心,长为半径作圆弧,交于点,以原点为圆心,长为半径画弧,交数轴于点,当点在点的右侧时,点对应的数是( )
A. B. C. D.
6.如图,已知中,,F是高和的交点,,,则线段的长度为( )
A.10 B.4 C.6 D.16
7.下列常见的数学符号可以看成是轴对称图形的是( )
A. B. C. D.
8.实数a、b的相反数分别为c、d,在数轴上点A、B、C、D分别表示数a、b、c、d,我们把A、D间的距离记为, B、C间的距离记为,则的大小关系为( )
A. B. C. D.不能确定
9.如图,中,与的平分线交于点,过点作交于点,交于点,那么下列结论不正确的是( )
A. B.
C.的周长等于与的和 D.和都是等腰三角形
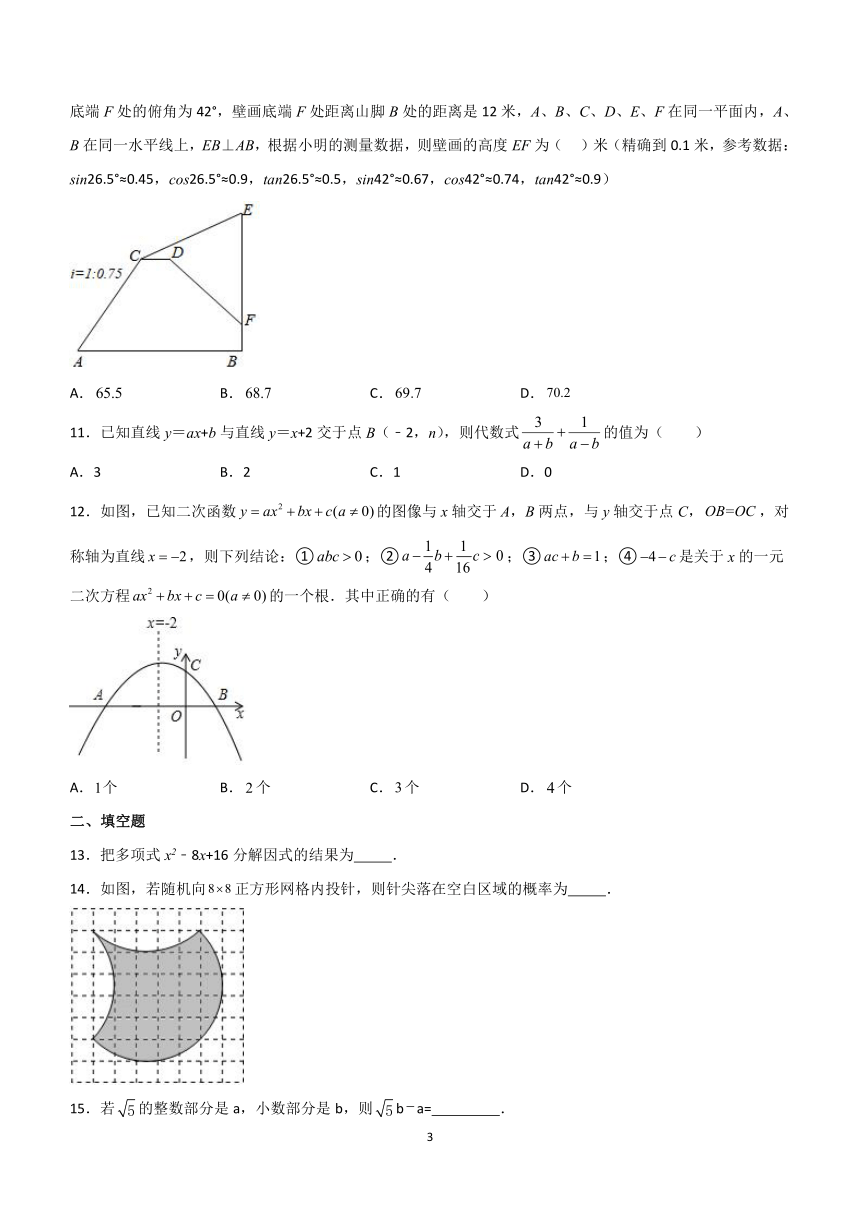
10.四面山是国家5A级风景区,里面有一个景点被誉为亚洲第一岩--土地神岩,土地神岩壁画高度从石岩F处开始一直竖直到山顶E处,为了测量土地神岩上壁画的高度,小明从山脚A处,沿坡度i=1:0.75的斜坡上行65米到达C处,在C处测得山顶E处仰角为26.5°,再往正前方水平走15米到达D处,在D处测得壁画底端F处的俯角为42°,壁画底端F处距离山脚B处的距离是12米,A、B、C、D、E、F在同一平面内,A、B在同一水平线上,EB⊥AB,根据小明的测量数据,则壁画的高度EF为( )米(精确到0.1米,参考数据:sin26.5°≈0.45,cos26.5°≈0.9,tan26.5°≈0.5,sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)
A. B. C. D.
11.已知直线y=ax+b与直线y=x+2交于点B(﹣2,n),则代数式的值为( )
A.3 B.2 C.1 D.0
12.如图,已知二次函数的图像与x轴交于A,B两点,与y轴交于点C,,对称轴为直线,则下列结论:①;②;③;④是关于x的一元二次方程的一个根.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
13.把多项式x2﹣8x+16分解因式的结果为 .
14.如图,若随机向正方形网格内投针,则针尖落在空白区域的概率为 .
15.若的整数部分是a,小数部分是b,则ba= .
16.已知关于的方程的根是,则 .
17.观察下列图形,它们是按一定规律排列的,依照此规律,第7个图形有 个.
18.如图,直角坐标系中,的顶点在轴上,,现将绕原点按顺时针方向旋转,得到,且点在轴上,则点的坐标是 .
三、解答题
19.计算:
(1)+-
(2)
20.(1)计算:(﹣)﹣2﹣6sin30°﹣(π﹣3.14)0﹣|﹣1|
(2)解不等式组:,并求出所有整数解之和.
21.在数学活动课上,小明提出这样一个问题:,E是的中点,平分,则平分,你认为小明的观点正确吗?请说明理由.
22.如图,已知点A、C分别在的边、上,且,//,与的平分线交于点D,连接.求证:平分.
23.某学校为了庆祝国庆节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元.
(1)求1盆A种花和1盆B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
24.如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(1)求反比例函数和直线EF:y=k2x+b的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b>的解集.
25.如图,一次函数的图象与反比例函数的图象相交于点两点.
(1)分别求出一次函数和反比例函数的解析式:
(2)根据图象,直接写出满足的的取值范围;
(3)连接BO并延长交双曲线于点C,连接AC,求ABC的面积.
26.已知,如图(1),a、b、c是△ABC的三边,且使得关于x的方程(b+c)x2+2ax﹣c+b=0有两个相等的实数根,同时使得关于x的方程x2+2ax+c2=0也有两个相等的实数根,D为B点关于AC的对称点.
(1)判断△ABC与四边形ABCD的形状并给出证明;
(2)P为AC上一点,且PM⊥PD,PM交BC于M,延长DP交AB于N,赛赛猜想CD、CM、CP三者之间的数量关系为CM+CD=CP,请你判断他的猜想是否正确,并给出证明;
(3)已知如图(2),Q为AB上一点,连接CQ,并将CQ逆时针旋转90°至CG,连接QG,H为GQ的中点,连接HD,试求出.
27.某市一中学组织学生参加防范电信网络诈骗知识竞赛活动.为了解活动的效果,学校从全校900名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等级:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图;
(2)这次测试成绩的中位数是什么等级?
(3)已知该市共有15000名中学生参加了这次防范电信网络诈骗知识竞赛,请你根据该学校的成绩估计该市在这次测试中成绩为优秀的人数;
(4)小王查了该市教育网站发现,全市参加本次测试的15000名学生中,成绩为优秀的有4000人,请你用所学统计知识简要说明实际优秀人数与估计优秀人数出现较大偏差的原因,并对该校在防范电信网络诈骗方面的教育给出简要的评价或建议.
参考答案
1.C
【详解】一次函数解析式形如+b,据此可知(1)y=πx,(2)y=2x-1是一次函数,共有2个,
故选C
2.D
【分析】根据题意画出树状图得出所有等情况数和第二次取出的球的号码不大于第一次取出的球的号码的情况数,然后根据概率公式即可得出答案.
【详解】解:根据题意画图如下:
由图可得,共有16种等情况数,其中第二次取出的球的号码不大于第一次取出的球的号码的有10种,
则第二次取出的球的号码不大于第一次取出的球的号码的概率为,
故答案为:D
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
3.C
【分析】由三视图还原成几何体即可判断.
【详解】解:根据所给几何体的三视图,可还原的几何体为:
故选:C.
【点睛】本题主要考查了由三视图还原几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.
4.B
【分析】根据科学记数法的定义:对于任意给定的实数,都可以写出,其中n为整数,进行求解即可得到答案.
【详解】解:1075用科学记数法可以表示为:
故选B.
【点睛】本题主要考查了科学记数法,解题的关键在于能够熟练掌握科学记数法的相关知识.
5.D
【分析】先依据勾股定理可求得的长,从而得到的长,于是可得到点M对应的数.
【详解】解:由题意得可知:,
根据勾股定理可知:
∴.
故选:D.
【点睛】本题主要考查的是实数与数轴,熟练掌握相关知识是解题的关键.
6.B
【分析】先证明,再证明,从而证明,利用全等三角形对应边相等就可得到答案.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
∵,,,
∴,
∵
∴
在和中,
,
∴,
∴.
故选:B.
【点睛】本题考查全等三角形的判定及全等三角形对应边相等的性质,解题关键在于正确寻找全等三角形.
7.A
【分析】本题考查了轴对称图形的判断,“如果一个图形沿一条直线折叠,两部分能完全重合,则这个图形叫作轴对称图形” ,据此即可求解.
【详解】解:在、、、四个数学符号中,是轴对称图形的是.
故选:A
8.B
【分析】此题考查了数轴与相反数,两点之间的距离的综合应用,根据题意得出,,把代入整理即可得出答案.
【详解】解:实数a、b的相反数分别为c、d,
,
在数轴上点A、B、C、D分别表示数a、b、c、d, A、D间的距离记为, B、C间的距离记为,
,
,
.
故选:B.
9.A
【分析】根据角平分线与平行线易得,从而可得,同理可得,由此可判断选项B、C、D正确,无法判断与的大小关系.
【详解】D.
,
是的平分线,是的平分线
,
,
和都是等腰三角形
∴D正确;
B.,都是等腰三角形
,
∴B.正确;
C.的周长
C正确;
A.不是等腰三角形
,
,
是错误的,
故选:A.
【点睛】本题考查等腰三角形的判定,掌握角平分线加平行线,可得等腰三角形这一几何模型是解题的关键.
10.C
【分析】如图,作CN⊥AB于N,延长CD交BE于M.解直角三角形分别求出MF、EM即可解决问题;
【详解】解:如图,作CN⊥AB于N,延长CD交BE于M.
在Rt△ACN中,AC=65m,CN:AN=1:0.75,
∴CN=52m,AN=39m,
∵四边形CNBM是矩形,
∴CN=BM=52m,
∵BF=12m,
∴FM=40m,
在Rt△DMF中,tan42°=,
∴DM=(m),
在Rt△CEM中,∵CM=CD+DM=m,
∴EM=CM tan26.5°=29.7(m),
∴EF=EM+FM=29.7+40=69.7(m),
故选:C.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
11.D
【分析】根据已知条件得到点B(﹣2,0),把点B(﹣2,0)代入y=ax+b得到﹣2a+b=0,代入代数式即可得到结论.
【详解】解:∵直线y=ax+b与直线y=x+2交于点B(﹣2,n),
∴n=0,
∴点B(﹣2,0),
把点B(﹣2,0)代入y=ax+b得,
﹣2a+b=0,
∴====0,
故选:D.
【点睛】本题考查了一次函数的性质,分式的化简求值,求得的关系是解题的关键.
12.C
【分析】利用抛物线开口方向得,利用对称轴方程得,利用图像与y轴交点位置得,则可对①进行判断;利用对称性可判断点A在点的左侧,当时,,可对②进行判断;利用点,,可得代入抛物线解析式可对③进行判断;利用对称性得代入抛物线解析式可对④进行判断;从而得出答案.
【详解】解:抛物线开口向下,
,
抛物线的对称轴为直线,
,
抛物线与y轴的交点在x轴上方,
,
,
故①正确;
点B到对称轴的距离大于2,
点A到对称轴的距离大于2,
点A在的左侧,
当时,,
,
,
故②正确;
,
,
,
,
故③错误;
点A与点B关于直线对称,
,
是关于x的一元二次方程的一个根,
故④正确;
故正确选项是①②④共3个.
故选C.
【点睛】此题主要考查了二次函数图像与系数的关系,抛物线与坐标轴交点,二次函数图像上点的坐标特征.熟练掌握二次函数的图像与性质是解题的关键.
13.(x﹣4)2
【分析】直接利用完全平方公式分解因式得出答案.
【详解】解:x2﹣8x+16=(x﹣4)2.
故答案为:(x﹣4)2.
【点睛】本题主要考查了分解因式,正确应用完全平方公式是解题关键.
14.
【分析】分别求出正方形的总面积和阴影部分的面积,用阴影部分的面积除以总面积即可得出概率.
【详解】解:∵,由平移可得,
∴针尖落在阴影部分的概率为.
故答案为:.
【点睛】本题考查的是几何概率,用到的知识点为:概率=相应的面积与总面积之比.
15..32
【详解】分析:先根据算术平方根的意义估算出的整数部分,即a的值,再根据b=-a故算出的小数部分b的值,然后代入ba到计算即可.
详解:∵4<5<9,
∴2<<3,
∴a=2,
∴b=-2,
∴原式=(2=32.
故答案为32.
点睛:本题考查了算术平方根的估算,熟练掌握原数=整数部分+小数部分和“夹逼法”是解答本题的关键.
16.
【分析】本题考查了求分式方程中的参数问题,把代入方程得,解方程即可求解,掌握分式方程的解法及理解方程的解的定义是解题的关键.
【详解】解:把代入方程得,,
方程两边同时乘以得,,
解得,
∵,
∴是原方程的解,
故答案为:.
17.71
【详解】观察图形、分析规律可知:各图形中“小太阳”的个数分别为:
图1:1+1;图2:2+2;图3:3+4;图4:4+8; ;图n:;
∴图7中“小太阳”的个数为:.
点睛:(1)第n个图形中第一行“小太阳”的个数为;(2)第n个图形中第二行“小太阳”的个数为.
18.
【分析】先求出AB的长,然后利用旋转的特点,得出OC、CD的长,从而得出点D的坐标.
【详解】∵△ABC是直角三角形,AO=5,OB=3,∠B=90°
∴AB=4
∵△ODC是△OAB旋转得到
∴OC=OB=3,CD=AB=4
∴D(3,4)
故答案为:(3,4)
【点睛】本题考查旋转的特点,注意旋转前后的图形是全等的.
19.(1)0
(2)
【分析】(1)根据有理数的乘方,算术平方根,立方根,求一个数的绝对值进行计算即可求解;
(2)根据有理数的乘方,算术平方根,立方根,化简的绝对值进行计算即可求解;
【详解】(1)解:原式=
;
(2)解:原式=
.
【点睛】本题考查了实数的混合运算,掌握有理数的乘方,算术平方根,立方根,化简的绝对值是解题的关键.
20.(1);(2)﹣3<x≤1,所有整数解的和:-2
【分析】(1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)求出每个不等式的解集,再确定其公共解,得到不等式组的整数解,求其和即可.
【详解】(1)(﹣)﹣2﹣6sin30°﹣(π﹣3.14)0﹣|﹣1|
=4﹣6×﹣1﹣(﹣1)
=4﹣3﹣1﹣+1
=1﹣;
(2)
解不等式①得:,
解不等式②得:,
∴原不等式组的解集是:,
∴原不等式组的整数解是﹣2,﹣1,0,1,
∴所有整数解的和:.
【点睛】本题主要考查了实数的运算,一元一次不等式组的解法,并会根据未知数的范围确定它所满足的特殊条件的值.一般方法是先解不等式组,再根据解集求出特殊值.
21.正确,理由见解析
【分析】延长交的延长线于点F,由,E是的中点,可证,从而,又由平分,易得,由三线合一可证平分.
【详解】解:如图,延长交的延长线于点F,
∵,E是的中点,
∴,
在和中,
,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴平分.
【点睛】此题考查了角平分线的定义、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
22.见解析
【分析】根据平行线的性质和角平分线的性质可得AC=AD,证明AB=AD,进而可以解决问题.
【详解】∵平分,
∴.
∵//,
∴,
∴,
∴.
∵
∴,
∴.
∵//,
∴,
∴,
∴平分.
【点睛】本题考查了等腰三角形的判定和性质,角平分线的定义,平行线的性质等知识,熟练掌握等腰三角形的判定和性质是解题的关键.
23.(1)1盆A种花的售价为3元,1盆B种花的售价是5元;(2)A种盆花最多购进66盆.
【分析】(1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据:“1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元”列方程组求解即可;
(2)首先根据“A种盆花的数量不超过B种盆花数量的2倍”确定m的取值范围,然后得出最值即可.
【详解】解:(1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据题意可得:
解得:
答:1盆A种花的售价为3元,1盆B种花的售价是5元;
(2)设购进A种花m盆,依据题意可得:
解得: 而为正整数,
∴m最多=66,
答:A种盆花最多购进66盆.
【点睛】此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键.
24.(1)反比例函数解析式为y=;直线EF的解析式为;(2);(3)<x<6.
【分析】(1)先利用矩形的性质确定C点坐标(6,4),再确定A点坐标为(3,2),根据反比例函数图象上点的坐标特征得到k1=6,即反比例函数解析式为y=;
(2)利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(,4),然后根据△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF进行计算;
(3)观察函数图象得到当<x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>.
【详解】(1)∵四边形DOBC是矩形,且点C的坐标为(6,4),
∴OB=6,OD=4,
∵点A为线段OC的中点,
∴A点坐标为(3,2),
∴k1=3×2=6,
∴反比例函数解析式为y=;
把x=6代入y=得y=1,则F点的坐标为(6,1);
把y=4代入y=得x=,则E点坐标为(,4),
把(6,1),(,4)代入y=k2x+b得,
解得,
所以直线EF的解析式为;
(2)△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF
=4×6-×4×-×6×1-×(6-)×(4-1)
=;
(3)由图象得:不等式不等式k2x+b>的解集为<x<6.
【点睛】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法确定函数解析式.
25.(1)反比例函数解析式为 ,次函数解析式为
(2)x≥4或-1≤x<0
(3)
【分析】(1)把A的坐标代入反比例函数的解析式,即可求反比例函数的解析式,把B的坐标代入求出B的坐标,把A、B的坐标代入一次函数即可求出函数的解析式;
(2)根据函数的图象和A、B的坐标即可得出答案;
(3)过C点作CDy轴,交直线AB于D,求出D的坐标,即可求得CD,然后根据 即可求出答案.
【详解】(1)解:∵反比例函数y=的图象经过点A(4,1),
∴ ,
∴反比例函数解析式为 ,
又点B(﹣1,n)在反比例函数上,
∴ ,
∴B的坐标为(-1,-4),
把A(4,1),B(﹣1,-4)代入 ,
得 ,
解得 ,
∴一次函数解析式为 ;
(2)解:由图象及交点坐标可知:
当x≥4或-1≤x<0时,k1x+b≥﹣;
(3)解:过C点作CDy轴,交直线AB于D,
∵B(-1,-4),B、C关于原点对称,
∴C(1,4),
把x=1代入y=x-3,得y=-2,
∴D(1,-2),CD=6,
∴.
【点睛】本题考查一次函数和反比例函数的交点问题,用待定系数法求一次函数的解析式,三角形的面积等知识点的综合运用,主要考查学生的计算能力和观察图形的能力,以及数形结合思想的运用.
26.(1)△ABC是等腰直角三角形.四边形ABCD是正方形;(2)猜想正确.(3)
【分析】(1)结论:△ABC是等腰直角三角形.四边形ABCD是正方形;根据根的判别式=0即可解决问题;
(2)猜想正确.如图1中,作PE⊥BC于E,PF⊥CD于F.只要证明△PEM≌△PFD即可解决问题;
(3)连接DG、CH,作QK⊥CD于K.则四边形BCKQ是矩形.只要证明△CKH≌△GDH,△DHK是等腰直角三角形即可解决问题.
【详解】解:(1)结论:△ABC是等腰直角三角形.四边形ABCD是正方形;
理由:∵关于x的方程(b+c)x2+2ax﹣c+b=0有两个相等的实数根,
∴4a2﹣4(b+c)(b﹣c)=0,
∴a2+c2=b2,
∴∠B=90°,
又∵关于x的方程x2+2ax+c2=0也有两个相等的实数根,
∴4a2﹣4c2=0,
∴a=c,
∴△ABC是等腰直角三角形,
∵D、B关于AC对称,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∵∠B=90°,
∴四边形ABCD是正方形.
(2)猜想正确.
理由:如图1中,作PE⊥BC于E,PF⊥CD于F.
∵四边形ABCD是正方形,
∴∠PCE=∠PCF=45°,
∵PE⊥CB,PF⊥CD,
∴PE=PF,
∵∠PFC=∠PEM=∠ECF=90°,PM⊥PD,
∴∠EPF=∠MPD=90°,四边形PECF是正方形,
∴∠MPE=∠DPF,
∴△PEM≌△PFD,
∴EM=DF,
∴CM+CCE﹣EM+CF+DF=2CF,
∵PC=CF,
∴CM+CD=PC.
(3)连接DG、CH,作QK⊥CD于K.则四边形BCKQ是矩形.
∵∠BCD=∠QCG=90°,
∴∠BCQ=∠DCG,
∵CB=CD,CQ=CG,
∴△CBQ≌△CDG,
∴∠CBQ=∠CDG=90°,BQ=DG=CK,
∵CQ=CG,QH=HG,
∴CH=HQ=HG,CH⊥QG,
∵∠CHO=∠GOD,∠COH=∠GOD,
∴∠HGD=∠HCK,
∴△CKH≌△GDH,
∴KH=DH,∠CHK=∠GHD,
∴∠CHG=∠KHD=90°,
∴△DHK是等腰直角三角形,
∴DK=AQ=DH,
∴.
【点睛】本题考查四边形综合题、正方形的性质和判定.等腰直角三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
27.(1)50人,画图见解析;(2)良好等级;(3)3000人;(4)见解析
【分析】(1)根据基本合格人数和已知百分比求出总人数,进而可求得合格的学生人数,计算出合格的频数即可补全频数分布直方图;
(2)根据中位数的定义判断即可;
(3)利用样本估计总体的思想解决问题即可
(4)根据样本是否具有代表性,即可说明实际优秀人数与估计人数出现较大偏差的原因,建议合理即可.
【详解】解:(1)被抽查的学生人数是30÷15%=200(人).
合格人数为200﹣30﹣80﹣40=50(人).
补全频数分布直方图如图:
(2)200个数据从小到大排列处在中间位置的两个数是第100、101位的两个数的平均数,
所以这次测试成绩的中位数会落在良好等级;
(3)(人),
答:该市获得优秀的学生有3000人;
(4)实际优秀人数与估计人数出现较大偏差的原因是该调查只抽查了全市一所中学的测试成绩,这个数据对于全市来讲不具有代表性.
建议:从数据可反映,该校的优秀率与全市的优秀率有明显差距,建议该校要对学生加强防范电信网络诈骗知识的学习.
【点睛】本题考查频数分布直方图,样本估计总体,扇形统计图,中位数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
一、单选题
1.下列函数(1)y=πx;(2)y=2x-1;(3) ;(4)y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
2.一个袋子中装有4个相同的小球,它们分别标有号码1,2,3,4,摇匀后随机取出一球,记下号码后放回:再将小球摇匀,并从袋中随机取出一球,则第二次取出的球的号码不大于第一次取出的球的号码的概率为( )
A. B. C. D.
3.一个水平放置的几何体的三视图如图所示,则这个几何体是( )
A.B.C.D.
4.改革开放之后,靠近上海的苏南地区凭借外向型产业快速发展,紧邻上海的苏州的工业经济也得以高速发展,吸引了大量人口进入,截止2019年3月苏州市常住人口为1075万人,1075用科学记数法表示为()
A. B. C. D.
5.如图,数轴上点、对应的数分别是1,2,过点作,以点为圆心,长为半径作圆弧,交于点,以原点为圆心,长为半径画弧,交数轴于点,当点在点的右侧时,点对应的数是( )
A. B. C. D.
6.如图,已知中,,F是高和的交点,,,则线段的长度为( )
A.10 B.4 C.6 D.16
7.下列常见的数学符号可以看成是轴对称图形的是( )
A. B. C. D.
8.实数a、b的相反数分别为c、d,在数轴上点A、B、C、D分别表示数a、b、c、d,我们把A、D间的距离记为, B、C间的距离记为,则的大小关系为( )
A. B. C. D.不能确定
9.如图,中,与的平分线交于点,过点作交于点,交于点,那么下列结论不正确的是( )
A. B.
C.的周长等于与的和 D.和都是等腰三角形
10.四面山是国家5A级风景区,里面有一个景点被誉为亚洲第一岩--土地神岩,土地神岩壁画高度从石岩F处开始一直竖直到山顶E处,为了测量土地神岩上壁画的高度,小明从山脚A处,沿坡度i=1:0.75的斜坡上行65米到达C处,在C处测得山顶E处仰角为26.5°,再往正前方水平走15米到达D处,在D处测得壁画底端F处的俯角为42°,壁画底端F处距离山脚B处的距离是12米,A、B、C、D、E、F在同一平面内,A、B在同一水平线上,EB⊥AB,根据小明的测量数据,则壁画的高度EF为( )米(精确到0.1米,参考数据:sin26.5°≈0.45,cos26.5°≈0.9,tan26.5°≈0.5,sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)
A. B. C. D.
11.已知直线y=ax+b与直线y=x+2交于点B(﹣2,n),则代数式的值为( )
A.3 B.2 C.1 D.0
12.如图,已知二次函数的图像与x轴交于A,B两点,与y轴交于点C,,对称轴为直线,则下列结论:①;②;③;④是关于x的一元二次方程的一个根.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
13.把多项式x2﹣8x+16分解因式的结果为 .
14.如图,若随机向正方形网格内投针,则针尖落在空白区域的概率为 .
15.若的整数部分是a,小数部分是b,则ba= .
16.已知关于的方程的根是,则 .
17.观察下列图形,它们是按一定规律排列的,依照此规律,第7个图形有 个.
18.如图,直角坐标系中,的顶点在轴上,,现将绕原点按顺时针方向旋转,得到,且点在轴上,则点的坐标是 .
三、解答题
19.计算:
(1)+-
(2)
20.(1)计算:(﹣)﹣2﹣6sin30°﹣(π﹣3.14)0﹣|﹣1|
(2)解不等式组:,并求出所有整数解之和.
21.在数学活动课上,小明提出这样一个问题:,E是的中点,平分,则平分,你认为小明的观点正确吗?请说明理由.
22.如图,已知点A、C分别在的边、上,且,//,与的平分线交于点D,连接.求证:平分.
23.某学校为了庆祝国庆节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元.
(1)求1盆A种花和1盆B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
24.如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(1)求反比例函数和直线EF:y=k2x+b的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b>的解集.
25.如图,一次函数的图象与反比例函数的图象相交于点两点.
(1)分别求出一次函数和反比例函数的解析式:
(2)根据图象,直接写出满足的的取值范围;
(3)连接BO并延长交双曲线于点C,连接AC,求ABC的面积.
26.已知,如图(1),a、b、c是△ABC的三边,且使得关于x的方程(b+c)x2+2ax﹣c+b=0有两个相等的实数根,同时使得关于x的方程x2+2ax+c2=0也有两个相等的实数根,D为B点关于AC的对称点.
(1)判断△ABC与四边形ABCD的形状并给出证明;
(2)P为AC上一点,且PM⊥PD,PM交BC于M,延长DP交AB于N,赛赛猜想CD、CM、CP三者之间的数量关系为CM+CD=CP,请你判断他的猜想是否正确,并给出证明;
(3)已知如图(2),Q为AB上一点,连接CQ,并将CQ逆时针旋转90°至CG,连接QG,H为GQ的中点,连接HD,试求出.
27.某市一中学组织学生参加防范电信网络诈骗知识竞赛活动.为了解活动的效果,学校从全校900名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等级:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图;
(2)这次测试成绩的中位数是什么等级?
(3)已知该市共有15000名中学生参加了这次防范电信网络诈骗知识竞赛,请你根据该学校的成绩估计该市在这次测试中成绩为优秀的人数;
(4)小王查了该市教育网站发现,全市参加本次测试的15000名学生中,成绩为优秀的有4000人,请你用所学统计知识简要说明实际优秀人数与估计优秀人数出现较大偏差的原因,并对该校在防范电信网络诈骗方面的教育给出简要的评价或建议.
参考答案
1.C
【详解】一次函数解析式形如+b,据此可知(1)y=πx,(2)y=2x-1是一次函数,共有2个,
故选C
2.D
【分析】根据题意画出树状图得出所有等情况数和第二次取出的球的号码不大于第一次取出的球的号码的情况数,然后根据概率公式即可得出答案.
【详解】解:根据题意画图如下:
由图可得,共有16种等情况数,其中第二次取出的球的号码不大于第一次取出的球的号码的有10种,
则第二次取出的球的号码不大于第一次取出的球的号码的概率为,
故答案为:D
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
3.C
【分析】由三视图还原成几何体即可判断.
【详解】解:根据所给几何体的三视图,可还原的几何体为:
故选:C.
【点睛】本题主要考查了由三视图还原几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.
4.B
【分析】根据科学记数法的定义:对于任意给定的实数,都可以写出,其中n为整数,进行求解即可得到答案.
【详解】解:1075用科学记数法可以表示为:
故选B.
【点睛】本题主要考查了科学记数法,解题的关键在于能够熟练掌握科学记数法的相关知识.
5.D
【分析】先依据勾股定理可求得的长,从而得到的长,于是可得到点M对应的数.
【详解】解:由题意得可知:,
根据勾股定理可知:
∴.
故选:D.
【点睛】本题主要考查的是实数与数轴,熟练掌握相关知识是解题的关键.
6.B
【分析】先证明,再证明,从而证明,利用全等三角形对应边相等就可得到答案.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
∵,,,
∴,
∵
∴
在和中,
,
∴,
∴.
故选:B.
【点睛】本题考查全等三角形的判定及全等三角形对应边相等的性质,解题关键在于正确寻找全等三角形.
7.A
【分析】本题考查了轴对称图形的判断,“如果一个图形沿一条直线折叠,两部分能完全重合,则这个图形叫作轴对称图形” ,据此即可求解.
【详解】解:在、、、四个数学符号中,是轴对称图形的是.
故选:A
8.B
【分析】此题考查了数轴与相反数,两点之间的距离的综合应用,根据题意得出,,把代入整理即可得出答案.
【详解】解:实数a、b的相反数分别为c、d,
,
在数轴上点A、B、C、D分别表示数a、b、c、d, A、D间的距离记为, B、C间的距离记为,
,
,
.
故选:B.
9.A
【分析】根据角平分线与平行线易得,从而可得,同理可得,由此可判断选项B、C、D正确,无法判断与的大小关系.
【详解】D.
,
是的平分线,是的平分线
,
,
和都是等腰三角形
∴D正确;
B.,都是等腰三角形
,
∴B.正确;
C.的周长
C正确;
A.不是等腰三角形
,
,
是错误的,
故选:A.
【点睛】本题考查等腰三角形的判定,掌握角平分线加平行线,可得等腰三角形这一几何模型是解题的关键.
10.C
【分析】如图,作CN⊥AB于N,延长CD交BE于M.解直角三角形分别求出MF、EM即可解决问题;
【详解】解:如图,作CN⊥AB于N,延长CD交BE于M.
在Rt△ACN中,AC=65m,CN:AN=1:0.75,
∴CN=52m,AN=39m,
∵四边形CNBM是矩形,
∴CN=BM=52m,
∵BF=12m,
∴FM=40m,
在Rt△DMF中,tan42°=,
∴DM=(m),
在Rt△CEM中,∵CM=CD+DM=m,
∴EM=CM tan26.5°=29.7(m),
∴EF=EM+FM=29.7+40=69.7(m),
故选:C.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
11.D
【分析】根据已知条件得到点B(﹣2,0),把点B(﹣2,0)代入y=ax+b得到﹣2a+b=0,代入代数式即可得到结论.
【详解】解:∵直线y=ax+b与直线y=x+2交于点B(﹣2,n),
∴n=0,
∴点B(﹣2,0),
把点B(﹣2,0)代入y=ax+b得,
﹣2a+b=0,
∴====0,
故选:D.
【点睛】本题考查了一次函数的性质,分式的化简求值,求得的关系是解题的关键.
12.C
【分析】利用抛物线开口方向得,利用对称轴方程得,利用图像与y轴交点位置得,则可对①进行判断;利用对称性可判断点A在点的左侧,当时,,可对②进行判断;利用点,,可得代入抛物线解析式可对③进行判断;利用对称性得代入抛物线解析式可对④进行判断;从而得出答案.
【详解】解:抛物线开口向下,
,
抛物线的对称轴为直线,
,
抛物线与y轴的交点在x轴上方,
,
,
故①正确;
点B到对称轴的距离大于2,
点A到对称轴的距离大于2,
点A在的左侧,
当时,,
,
,
故②正确;
,
,
,
,
故③错误;
点A与点B关于直线对称,
,
是关于x的一元二次方程的一个根,
故④正确;
故正确选项是①②④共3个.
故选C.
【点睛】此题主要考查了二次函数图像与系数的关系,抛物线与坐标轴交点,二次函数图像上点的坐标特征.熟练掌握二次函数的图像与性质是解题的关键.
13.(x﹣4)2
【分析】直接利用完全平方公式分解因式得出答案.
【详解】解:x2﹣8x+16=(x﹣4)2.
故答案为:(x﹣4)2.
【点睛】本题主要考查了分解因式,正确应用完全平方公式是解题关键.
14.
【分析】分别求出正方形的总面积和阴影部分的面积,用阴影部分的面积除以总面积即可得出概率.
【详解】解:∵,由平移可得,
∴针尖落在阴影部分的概率为.
故答案为:.
【点睛】本题考查的是几何概率,用到的知识点为:概率=相应的面积与总面积之比.
15..32
【详解】分析:先根据算术平方根的意义估算出的整数部分,即a的值,再根据b=-a故算出的小数部分b的值,然后代入ba到计算即可.
详解:∵4<5<9,
∴2<<3,
∴a=2,
∴b=-2,
∴原式=(2=32.
故答案为32.
点睛:本题考查了算术平方根的估算,熟练掌握原数=整数部分+小数部分和“夹逼法”是解答本题的关键.
16.
【分析】本题考查了求分式方程中的参数问题,把代入方程得,解方程即可求解,掌握分式方程的解法及理解方程的解的定义是解题的关键.
【详解】解:把代入方程得,,
方程两边同时乘以得,,
解得,
∵,
∴是原方程的解,
故答案为:.
17.71
【详解】观察图形、分析规律可知:各图形中“小太阳”的个数分别为:
图1:1+1;图2:2+2;图3:3+4;图4:4+8; ;图n:;
∴图7中“小太阳”的个数为:.
点睛:(1)第n个图形中第一行“小太阳”的个数为;(2)第n个图形中第二行“小太阳”的个数为.
18.
【分析】先求出AB的长,然后利用旋转的特点,得出OC、CD的长,从而得出点D的坐标.
【详解】∵△ABC是直角三角形,AO=5,OB=3,∠B=90°
∴AB=4
∵△ODC是△OAB旋转得到
∴OC=OB=3,CD=AB=4
∴D(3,4)
故答案为:(3,4)
【点睛】本题考查旋转的特点,注意旋转前后的图形是全等的.
19.(1)0
(2)
【分析】(1)根据有理数的乘方,算术平方根,立方根,求一个数的绝对值进行计算即可求解;
(2)根据有理数的乘方,算术平方根,立方根,化简的绝对值进行计算即可求解;
【详解】(1)解:原式=
;
(2)解:原式=
.
【点睛】本题考查了实数的混合运算,掌握有理数的乘方,算术平方根,立方根,化简的绝对值是解题的关键.
20.(1);(2)﹣3<x≤1,所有整数解的和:-2
【分析】(1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)求出每个不等式的解集,再确定其公共解,得到不等式组的整数解,求其和即可.
【详解】(1)(﹣)﹣2﹣6sin30°﹣(π﹣3.14)0﹣|﹣1|
=4﹣6×﹣1﹣(﹣1)
=4﹣3﹣1﹣+1
=1﹣;
(2)
解不等式①得:,
解不等式②得:,
∴原不等式组的解集是:,
∴原不等式组的整数解是﹣2,﹣1,0,1,
∴所有整数解的和:.
【点睛】本题主要考查了实数的运算,一元一次不等式组的解法,并会根据未知数的范围确定它所满足的特殊条件的值.一般方法是先解不等式组,再根据解集求出特殊值.
21.正确,理由见解析
【分析】延长交的延长线于点F,由,E是的中点,可证,从而,又由平分,易得,由三线合一可证平分.
【详解】解:如图,延长交的延长线于点F,
∵,E是的中点,
∴,
在和中,
,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴平分.
【点睛】此题考查了角平分线的定义、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
22.见解析
【分析】根据平行线的性质和角平分线的性质可得AC=AD,证明AB=AD,进而可以解决问题.
【详解】∵平分,
∴.
∵//,
∴,
∴,
∴.
∵
∴,
∴.
∵//,
∴,
∴,
∴平分.
【点睛】本题考查了等腰三角形的判定和性质,角平分线的定义,平行线的性质等知识,熟练掌握等腰三角形的判定和性质是解题的关键.
23.(1)1盆A种花的售价为3元,1盆B种花的售价是5元;(2)A种盆花最多购进66盆.
【分析】(1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据:“1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元”列方程组求解即可;
(2)首先根据“A种盆花的数量不超过B种盆花数量的2倍”确定m的取值范围,然后得出最值即可.
【详解】解:(1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据题意可得:
解得:
答:1盆A种花的售价为3元,1盆B种花的售价是5元;
(2)设购进A种花m盆,依据题意可得:
解得: 而为正整数,
∴m最多=66,
答:A种盆花最多购进66盆.
【点睛】此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键.
24.(1)反比例函数解析式为y=;直线EF的解析式为;(2);(3)<x<6.
【分析】(1)先利用矩形的性质确定C点坐标(6,4),再确定A点坐标为(3,2),根据反比例函数图象上点的坐标特征得到k1=6,即反比例函数解析式为y=;
(2)利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(,4),然后根据△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF进行计算;
(3)观察函数图象得到当<x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>.
【详解】(1)∵四边形DOBC是矩形,且点C的坐标为(6,4),
∴OB=6,OD=4,
∵点A为线段OC的中点,
∴A点坐标为(3,2),
∴k1=3×2=6,
∴反比例函数解析式为y=;
把x=6代入y=得y=1,则F点的坐标为(6,1);
把y=4代入y=得x=,则E点坐标为(,4),
把(6,1),(,4)代入y=k2x+b得,
解得,
所以直线EF的解析式为;
(2)△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF
=4×6-×4×-×6×1-×(6-)×(4-1)
=;
(3)由图象得:不等式不等式k2x+b>的解集为<x<6.
【点睛】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法确定函数解析式.
25.(1)反比例函数解析式为 ,次函数解析式为
(2)x≥4或-1≤x<0
(3)
【分析】(1)把A的坐标代入反比例函数的解析式,即可求反比例函数的解析式,把B的坐标代入求出B的坐标,把A、B的坐标代入一次函数即可求出函数的解析式;
(2)根据函数的图象和A、B的坐标即可得出答案;
(3)过C点作CDy轴,交直线AB于D,求出D的坐标,即可求得CD,然后根据 即可求出答案.
【详解】(1)解:∵反比例函数y=的图象经过点A(4,1),
∴ ,
∴反比例函数解析式为 ,
又点B(﹣1,n)在反比例函数上,
∴ ,
∴B的坐标为(-1,-4),
把A(4,1),B(﹣1,-4)代入 ,
得 ,
解得 ,
∴一次函数解析式为 ;
(2)解:由图象及交点坐标可知:
当x≥4或-1≤x<0时,k1x+b≥﹣;
(3)解:过C点作CDy轴,交直线AB于D,
∵B(-1,-4),B、C关于原点对称,
∴C(1,4),
把x=1代入y=x-3,得y=-2,
∴D(1,-2),CD=6,
∴.
【点睛】本题考查一次函数和反比例函数的交点问题,用待定系数法求一次函数的解析式,三角形的面积等知识点的综合运用,主要考查学生的计算能力和观察图形的能力,以及数形结合思想的运用.
26.(1)△ABC是等腰直角三角形.四边形ABCD是正方形;(2)猜想正确.(3)
【分析】(1)结论:△ABC是等腰直角三角形.四边形ABCD是正方形;根据根的判别式=0即可解决问题;
(2)猜想正确.如图1中,作PE⊥BC于E,PF⊥CD于F.只要证明△PEM≌△PFD即可解决问题;
(3)连接DG、CH,作QK⊥CD于K.则四边形BCKQ是矩形.只要证明△CKH≌△GDH,△DHK是等腰直角三角形即可解决问题.
【详解】解:(1)结论:△ABC是等腰直角三角形.四边形ABCD是正方形;
理由:∵关于x的方程(b+c)x2+2ax﹣c+b=0有两个相等的实数根,
∴4a2﹣4(b+c)(b﹣c)=0,
∴a2+c2=b2,
∴∠B=90°,
又∵关于x的方程x2+2ax+c2=0也有两个相等的实数根,
∴4a2﹣4c2=0,
∴a=c,
∴△ABC是等腰直角三角形,
∵D、B关于AC对称,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∵∠B=90°,
∴四边形ABCD是正方形.
(2)猜想正确.
理由:如图1中,作PE⊥BC于E,PF⊥CD于F.
∵四边形ABCD是正方形,
∴∠PCE=∠PCF=45°,
∵PE⊥CB,PF⊥CD,
∴PE=PF,
∵∠PFC=∠PEM=∠ECF=90°,PM⊥PD,
∴∠EPF=∠MPD=90°,四边形PECF是正方形,
∴∠MPE=∠DPF,
∴△PEM≌△PFD,
∴EM=DF,
∴CM+CCE﹣EM+CF+DF=2CF,
∵PC=CF,
∴CM+CD=PC.
(3)连接DG、CH,作QK⊥CD于K.则四边形BCKQ是矩形.
∵∠BCD=∠QCG=90°,
∴∠BCQ=∠DCG,
∵CB=CD,CQ=CG,
∴△CBQ≌△CDG,
∴∠CBQ=∠CDG=90°,BQ=DG=CK,
∵CQ=CG,QH=HG,
∴CH=HQ=HG,CH⊥QG,
∵∠CHO=∠GOD,∠COH=∠GOD,
∴∠HGD=∠HCK,
∴△CKH≌△GDH,
∴KH=DH,∠CHK=∠GHD,
∴∠CHG=∠KHD=90°,
∴△DHK是等腰直角三角形,
∴DK=AQ=DH,
∴.
【点睛】本题考查四边形综合题、正方形的性质和判定.等腰直角三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
27.(1)50人,画图见解析;(2)良好等级;(3)3000人;(4)见解析
【分析】(1)根据基本合格人数和已知百分比求出总人数,进而可求得合格的学生人数,计算出合格的频数即可补全频数分布直方图;
(2)根据中位数的定义判断即可;
(3)利用样本估计总体的思想解决问题即可
(4)根据样本是否具有代表性,即可说明实际优秀人数与估计人数出现较大偏差的原因,建议合理即可.
【详解】解:(1)被抽查的学生人数是30÷15%=200(人).
合格人数为200﹣30﹣80﹣40=50(人).
补全频数分布直方图如图:
(2)200个数据从小到大排列处在中间位置的两个数是第100、101位的两个数的平均数,
所以这次测试成绩的中位数会落在良好等级;
(3)(人),
答:该市获得优秀的学生有3000人;
(4)实际优秀人数与估计人数出现较大偏差的原因是该调查只抽查了全市一所中学的测试成绩,这个数据对于全市来讲不具有代表性.
建议:从数据可反映,该校的优秀率与全市的优秀率有明显差距,建议该校要对学生加强防范电信网络诈骗知识的学习.
【点睛】本题考查频数分布直方图,样本估计总体,扇形统计图,中位数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
同课章节目录
