2024年湖南省长沙市中考数学高频易错题精选练习(二)(含解析)
文档属性
| 名称 | 2024年湖南省长沙市中考数学高频易错题精选练习(二)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:46:32 | ||
图片预览


文档简介
2024年湖南省长沙市中考数学高频易错题精选练习(二)
一、单选题
1.下列四个数:,,,中,绝对值最大的数是( ).
A. B. C. D.
2.电影《长津湖》备受观众喜爱,截止到2021年12月初,累计票房57.44亿元,57.44亿元用科学记数法表示为( )
A. B. C. D.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
4.下列四个命题中,真命题有( )
①一个三角形中至少有两个锐角. ②如果是的对顶角,那么.
③如果a为实数,那么. ④实数与数轴上的点是一一对应的.
⑤0.3,0.4,0.5是一组勾股数.
A.1个 B.2个 C.3个 D.4个
5.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心.若,则这个正多边形的边数为( )
A.7 B.8 C.9 D.10
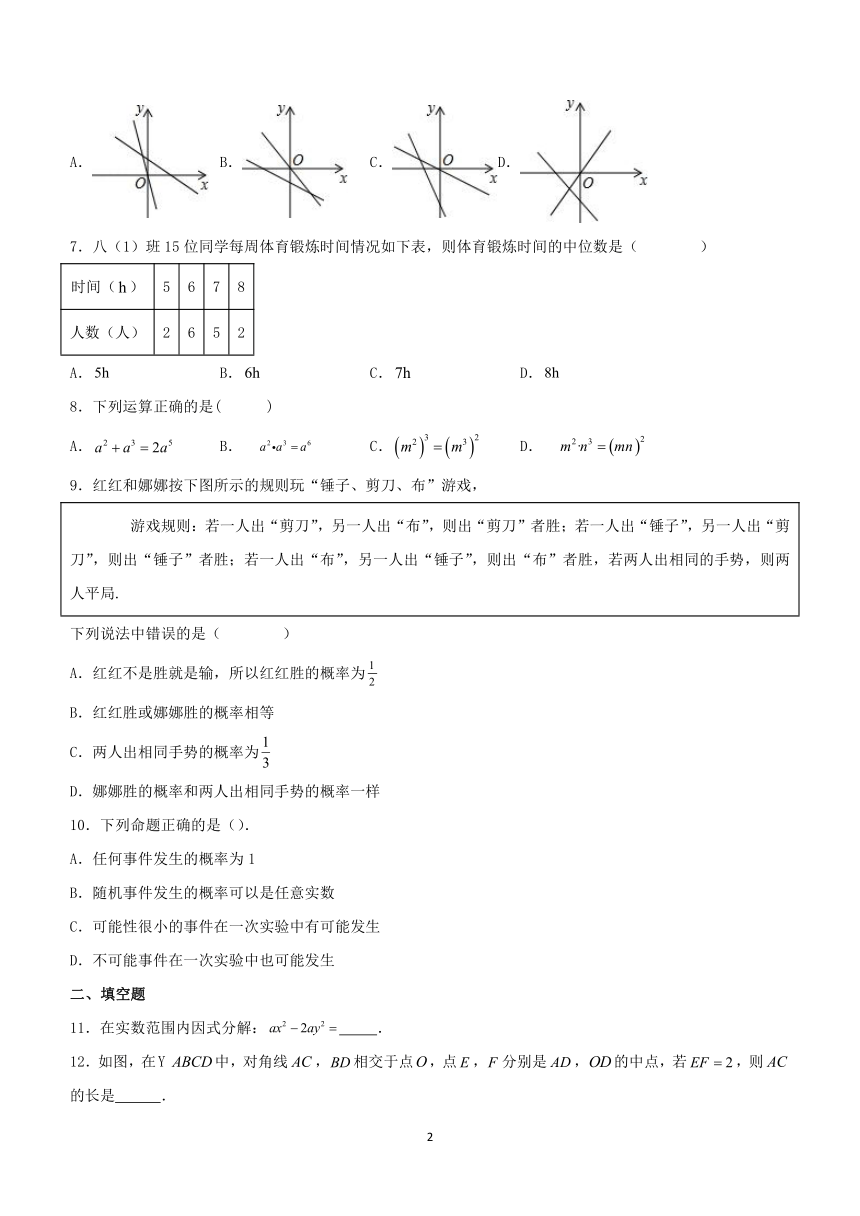
6.在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )
A. B. C.D.
7.八(1)班15位同学每周体育锻炼时间情况如下表,则体育锻炼时间的中位数是( )
时间() 5 6 7 8
人数(人) 2 6 5 2
A. B. C. D.
8.下列运算正确的是( )
A. B. C. D.
9.红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是( )
A.红红不是胜就是输,所以红红胜的概率为
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
D.娜娜胜的概率和两人出相同手势的概率一样
10.下列命题正确的是().
A.任何事件发生的概率为1
B.随机事件发生的概率可以是任意实数
C.可能性很小的事件在一次实验中有可能发生
D.不可能事件在一次实验中也可能发生
二、填空题
11.在实数范围内因式分解: .
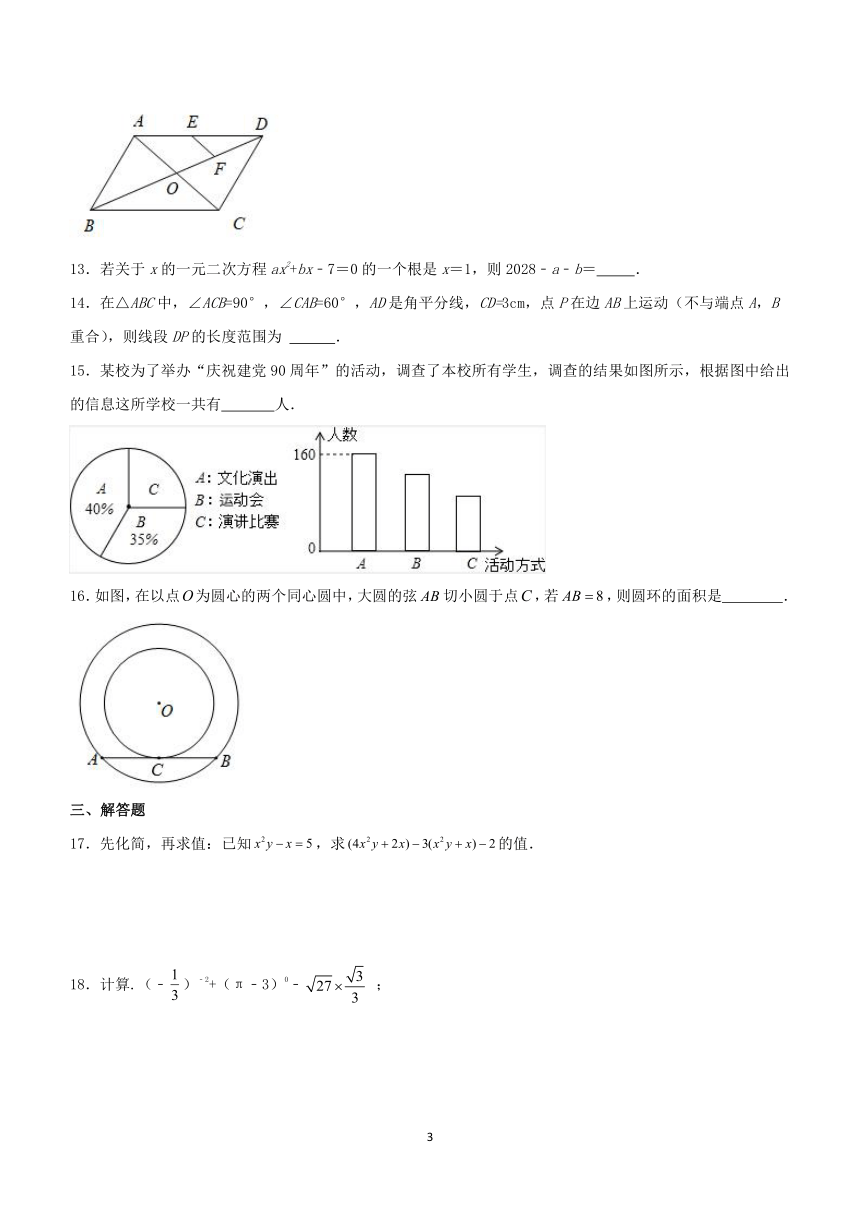
12.如图,在中,对角线,相交于点,点,分别是,的中点,若,则的长是 .
13.若关于x的一元二次方程ax2+bx﹣7=0的一个根是x=1,则2028﹣a﹣b= .
14.在△ABC中,∠ACB=90°,∠CAB=60°,AD是角平分线,CD=3cm,点P在边AB上运动(不与端点A,B重合),则线段DP的长度范围为 .
15.某校为了举办“庆祝建党90周年”的活动,调查了本校所有学生,调查的结果如图所示,根据图中给出的信息这所学校一共有 人.
16.如图,在以点为圆心的两个同心圆中,大圆的弦切小圆于点,若,则圆环的面积是 .
三、解答题
17.先化简,再求值:已知,求的值.
18.计算.(﹣)﹣2+(π﹣3)0﹣ ;
19.如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
20.
(1)如图1,在中,,,求的面积;
(2)我市将在春天举办花展,政府为花展划定了一个三角形区域,米,米.根据需要,政府将花展区域内的区域划定为管理区域,禁止游客进入.其中点D,E分别在,边上,米,米.主办方在四边形内部摆满鲜花,其中在边上摆满郁金香.某游客想要拍摄AD边上的郁金香,且已知拍摄的张角等于时,拍照效果最佳.请你帮该游客在四边形的边上寻找最佳拍摄地点P,并求此时的长度.()
21.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是___;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是___;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
22.列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 答对题数 答错题数 得分
小明 10 10 40
小红 19 1 94
小刚 20 0 100
小强 18 2 88
小丽 14 6 64
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?
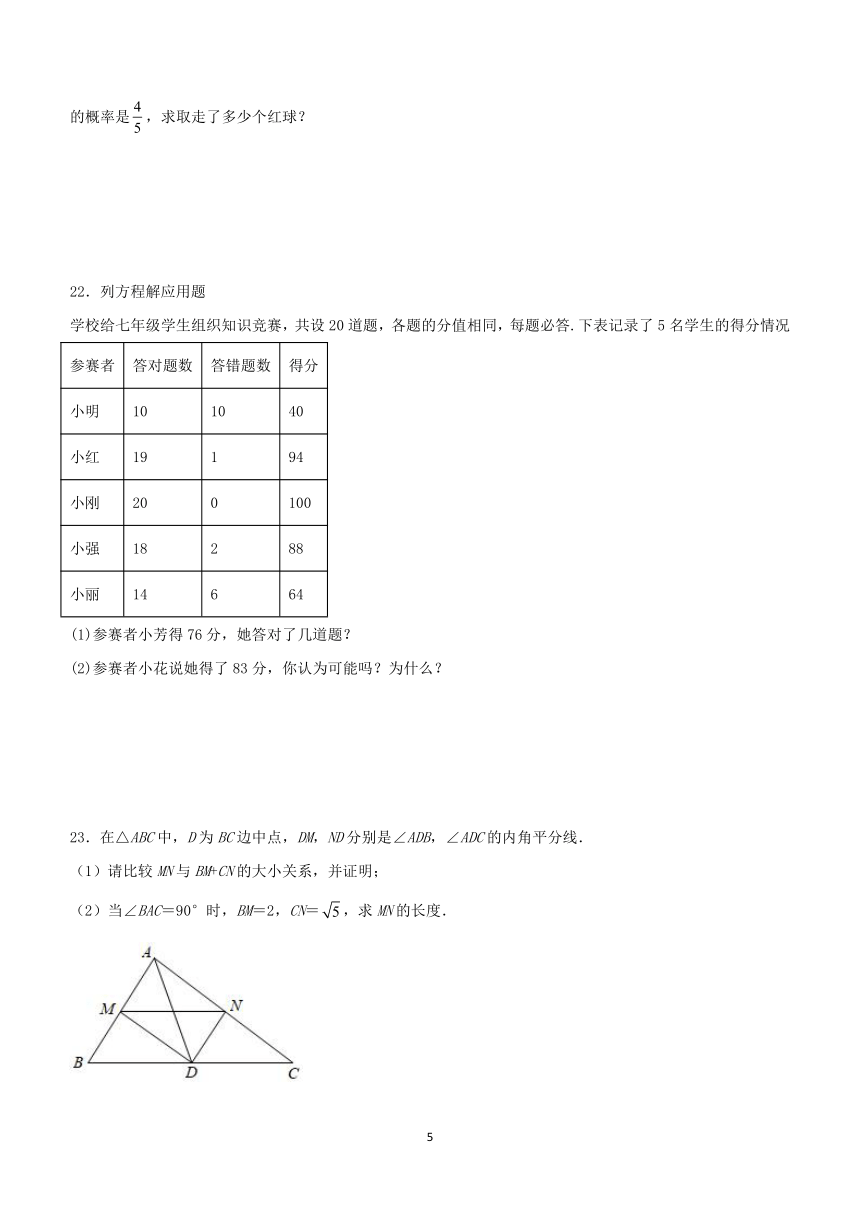
23.在△ABC中,D为BC边中点,DM,ND分别是∠ADB,∠ADC的内角平分线.
(1)请比较MN与BM+CN的大小关系,并证明;
(2)当∠BAC=90°时,BM=2,CN=,求MN的长度.
24.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C,B点的坐标为(6,0),点M为抛物线上的一个动点.
(1)若该二次函数图象的对称轴为直线x=4时:
①求二次函数的表达式;
②当点M位于x轴下方抛物线图象上时,过点M作x轴的垂线,交BC于点Q,求线段MQ的最大值;
(2)过点M作BC的平行线,交抛物线于点N,设点M、N的横坐标为m、n.在点M运动的过程中,试问m+n的值是否会发生改变?若改变,请说明理由;若不变,请求出m+n的值.
25.如图,在△ABC中,AB=AC=2,∠BAC=120°,点D为BC上一动点(不与B、C重合),E是AD延长线上的一点,且∠BCE=∠BAD.
(1)求∠AEC的度数;
(2)试说明:在点D运动的过程中,∠AEB的度数是一个定值;
(3)若AD=a,DE=b,求ab的最大值.
参考答案
1.A
【分析】先求出负数的绝对值的大小,再进行实数的比较即可.
【详解】∵,,,.
∴.
∴绝对值最大的数为-4.
故选A.
【点睛】本题考查实数大小的比较方法以及绝对值的性质.掌握“正数的绝对值是它本身,负数的绝对值是它的相反数”是解答本题的关键.
2.C
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【详解】解:57.44亿用科学记数法表示为,故C正确.
故选:C.
【点睛】本题考查用科学记数法表示较大的数,一般形式为,其中,n可以用整数位数减去1来确定.用科学记数法表示数,一定要注意a的形式,以及指数n的确定方法.
3.B
【分析】根据轴对称图形和中心对称图形的定义,即可进行解答;轴对称图形:沿对称轴折叠后两部分可重合的图形;中心对称图形:绕旋转中心旋转180度后与原图重合的图形.
【详解】解:A.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
B.原图既是轴对称图形,又是中心对称图形,故此选项符合题意;
C.原图既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:B.
【点睛】此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.C
【分析】根据三角形内角的性质、对顶角的定义、绝对值的性质、数轴的定义、勾股数的定义进行判断即可.
【详解】解:①一个三角形中至少有两个锐角,正确,为真命题;
②如果是的对顶角,那么,正确,为真命题;
③当时,,故③错误,为假命题;
④实数与数轴上的点是一一对应的,正确,为真命题;
⑤勾股数需为正整数,故⑤错误,为假命题;
故选:C.
【点睛】本题考查了命题与定理的知识,熟练掌握勾股数的定义、数轴的定义、绝对值的性质及对顶角的定义和三角形内角的性质是解题的关键.
5.C
【分析】连接,,根据圆周角定理得到,进一步即可得到结论.
【详解】解:连接,,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,为半径的同一个圆上,
∵,
∴,
∴这个正多边形的边数,
故选:C.
【点睛】本题考查了正多边形与圆,圆周角定理,正确地理解题意是解题的关键.
6.C
【分析】根据正比例函数与一次函数的图象性质作答.
【详解】解:当k>2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,3象限;
当0<k<2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,4象限;
当k<0时,正比例函数y=kx图象经过2,4象限,一次函数y=(k﹣2)x+k的图象2,3,4象限,当(k﹣2)x+k=kx时,x=<0,所以两函数交点的横坐标小于0.
故选C.
【点睛】本题考查一次函数的图象性质,正比例函数的图象性质,关键是由k的取值确定函数所在的象限.
7.B
【分析】根据中位数的定义进行解答即可.
【详解】解:∵共有15个数,最中间的数是8个数,
∴这15名同学一周在校参加体育锻炼时间的中位数是6;
故选:B.
【点睛】此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
8.C
【分析】根据合并同类项法则,同底数幂的乘法,幂的乘方,积的乘方运算逐项计算排除即可.
【详解】、与不是同类项,不可以合并,此选项计算错误,不符合题意;
、,此选项计算错误,不符合题意;
、,此选项计算正确,符合题意;
、,此选项计算错误,不符合题意;
故选:.
【点睛】此题考查了整式的运算,解题的关键是熟练掌握合并同类项法则,同底数幂的乘法,幂的乘方,积的乘方运算及其应用.
9.A
【详解】试题解析:红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
红红娜娜 锤子 剪刀 布
锤子 (锤子,锤子) (锤子,剪刀) (锤子,布)
剪刀 (剪刀,锤子) (剪刀,剪刀) (剪刀,布)
布 (布,锤子) (布,剪刀) (布,布)
由表格可知,共有9种等可能情况.其中平局的有3种:(锤子,锤子)、(剪刀,剪刀)、(布,布).
因此,红红和娜娜两人出相同手势的概率为,两人获胜的概率都为,
红红不是胜就是输,所以红红胜的概率为,错误,故选项A符合题意,
故选项B,C,D不合题意;
故选A.
10.C
【分析】根据随机事件、不可能事件的定义和概率的性质判断各选项即可.
【详解】A中,只有必然事件概率才是1,错误;
B中,随机事件的概率p取值范围为:0<p<1,错误;
C中,可能性很小的事件,是有可能发生的,正确;
D中,不可能事件一定不发生,错误
故选:C
【点睛】本题考查事件的可能性,注意,任何事件的概率P一定在0至1之间.
11.
【分析】利用提公因式法和平方差公式即可解答.
【详解】
故答案为:.
【点睛】此题主要考查了实属范围内分解因式,采用提公因式法和平方差公式是解答本题的关键.
12.8
【分析】首先根据平行四边形的性质得出,再说明EF是△ADO的中位线,得出,即可求得答案.
【详解】∵四边形ABCD为平行四边形,
∴,
又∵E,F为AD,OD的中点,
∴,
∴,
∴,
故填:8.
【点睛】本题考查平行四边形的性质,三角形的中位线的判定和性质,熟练掌握平行四边形和三角形中位线的性质是解题关键.
13.2021
【分析】根据一元二次方程的解的定义,把x=1代入方程得到a+b﹣7=0,于是得a+b的值,再代入计算2028﹣a﹣b的值.
【详解】解:把x=1代入ax2+bx﹣7=0得a+b﹣7=0,
∴a+b=7
∴2028﹣a﹣b=2028-(a+b)=2021.
故答案为:2021.
【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
14.3≤DP<6
【分析】根据角平分线的定义得到∠CAD=∠BAD=30°,根据直角三角形的性质得到AD=2CD=6,过D作DP⊥AB于P,PD=AD=3,于是得到结论.
【详解】解:如图,
∵∠CAB=60°,AD是角平分线,
∴∠CAD=∠BAD=30°,
∵∠ACB=90°,CD=3,
∴AD=2CD=6,
过D作DP⊥AB于P,
∴∠APD=90°,
∴PD=AD=3,
∴线段DP的长度范围为3≤DP<6,
故答案为:3≤DP<6.
【点睛】本题考查了含30°角的直角三角形的性质、角平分线的定义,正确的作出辅助线是解题的关键.
15.400
【分析】根据A文艺演出的人数及所占的比例即可得出总人数,
【详解】解:160÷40%=400(人).
则这所学校一共有400人
故答案为:400.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
16.
【分析】如图,连接、,设,,由切线的性质得,,由垂径定理得,,由勾股定理得,,由即可求出圆环的面积.
【详解】
如图,连接、,设,,
大圆的弦切小圆于点,
,
,
,
在中,,
,,
,
故答案为:.
【点睛】本题考查了切线的性质、垂径定理、勾股定理以及圆与圆环的面积计算,掌握圆的相关知识是解题的关键.
17.,.
【分析】先去括号,再合并同类项,然后整体代入求值即可.
【详解】解:
=
=.
当时,
原式=
=
【点睛】本题考查了整式的化简求值,解题关键是熟练运用整式加减法则进行化简,整体代入求值.
18.7
【分析】根据负整数指数幂、零指数幂和二次根式的乘法可以解答本题.
【详解】解:(﹣)﹣2+(π﹣3)0﹣
=9+1﹣
=9+1﹣3
=7
【点睛】本题主要考查实数的混合运算,掌握负整数指数幂、零指数幂和二次根式的乘法的运算法则是关键.
19.(1)见解析;(2)见解析
【分析】(1)以点B为圆心,任意长为半径画弧与AB、BC相交,再分别以两个交点为圆心,大于两点间距离的一半为半径,在角的内部相交于一点,连接此点与点B并延长交AC与点D;
(2)根据已知条件证明△DBE≌△DBC,即可得到结论.
【详解】(1)作图如图所示,
(2)证明:∵平分,
∴,
又∵,,
∴,
∴.
【点睛】此题考查了基本作图--角平分线的画法,以及三角形全等的判定及性质.解题关键是掌握基本作图.
20.(1)
(2)取点见解析,100或
【分析】对于(1),先说明是等边三角形,再根据勾股定理求出高,根据三角形的面积计算即可;
对于(2),当点P在上时,根据“两角分别相等的三角形相似”得,再根据相似三角形的对应边长比例得,然后代入数值得出答案;当点P在上时,利用平行线分线段成比例定理得到,即,解方程即可.
【详解】(1)∵,,
∴是等边三角形,
∴.
过点A作,于点F,
∴.
根据勾股定理,得.
∴;
(2)解:如图所示,当点P在上时,
∵,
∴.
∵,,
∴,
∴,
∴,
即,
解得或,
当时,,不符合题意;
∴米;
当点P在上时,
∵,
∴,
∴,即,
∴米,
综上所述,的长为100米或米
【点睛】本题主要考查了等边三角形的性质和判定,等腰三角形的性质,相似三角形的性质和判定,灵活选择判定定理是解题的关键.
21.(1)0
(2)
(3)4个
【详解】(1)解:∵口袋中装有4个白球和6个红球,
∴从口袋中随机摸出一个球是绿球是不可能事件,
发生的概率为0;
故答案为:0;
(2)解:∵口袋中装有4个白球和6个红球,共有10个球,
∴从口袋中随机摸出一个球是红球的概率是=;
故答案为:;
(3)解:设取走了x个红球,根据题意得:
,
解得:x=4,
答:取走了4个红球.
【点睛】此题考查了用概率公式求事件概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
22.(1)小芳答对了16道题;(2)小花不可能的83分,理由见解析.
【分析】根据表格得出答对一题得5分,再算出错一题扣1分,
(1)设小芳答对了m道题,答错了(20-m)道题,根据答对的得分+加上答错的得分=76分建立方程求出其解即可;
(2)假设小花得83分可能,设答对了y道题,答错了(20-y)道题,根据答对的得分+加上答错的得分=83分建立方程求出其解即可.
【详解】由小刚可得答对一题得5分
设答错一题得x分,10x+50=40(或19×5+x=94或18×5+2x=88或14×5+6x=64)
x=-1
(1)设小芳答对了m道题,则答错(20-m)道题
5m-(20-m)=76
m=16
答小芳答对了16道题
(2)不可能.
假设可能,设小花答对了y道题,则答错了(20-y)道题
5y-(20-y)=83
y=
因为不是整数
所以假设不成立
所以小花不可能的83分
【点睛】本题考查了列一元一次方程解实际问题的运用,结论猜想试题的运用,解答时关键答对的得分+加上答错的得分=总得分是关键.
23.(1)BM+CN>MN,理由见解析;(2)3
【分析】(1)如图,延长ND到H,使ND=DH,连接MH,BH,由“SAS”可证△CDN≌△BDH,可得BH=CN,DH=DN,∠ACB=∠DBH,由线段垂直平分线的性质可得MN=MH,由三角形的三边关系可求解;
(2)先证明∠ABH=90°,在Rt△BHM中,由勾股定理可求MH的长,即可求解.
【详解】解:(1)BM+CN>MN,
理由如下:如图,延长ND到H,使ND=DH,连接MH,BH,
∵点D是BC的中点,
∴BD=CD,
在△CDN和△BDH中,
,
∴△CDN≌△BDH(SAS),
∴BH=CN,DH=DN,∠ACB=∠DBH,
∵DM,ND分别是∠ADB,∠ADC的内角平分线,
∴∠ADM=∠ADB,∠ADN=∠ADC,
∴∠ADM+∠ADN=90°,
∴∠MDN=90°,
∴MH=MN,
在△BMH中,BM+BH>MH,
∴BM+CN>MN;
(2)∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
∴∠ABC+∠DBH=90°,
∴∠HBM=90°,
∵BM=2,BH=CN=,
∴MH==3,
∴MN=MH=3.
【点睛】本题考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,添加恰当辅助线构造全等三角形是解题的关键.
24.(1)①y=x2﹣8x+12;②线段MQ的最大值为9.(2)m+n的值为定值.m+n=6.
【分析】(1)①根据点B的坐标和二次函数图象的对称轴即可求出二次函数解析式;
②设M(m,m2﹣8m+12),利用待定系数法求出直线BC的解析式,从而求出Q(m,﹣2m+12),即可求出MQ的长与m的函数关系式,然后利用二次函数求最值即可;
(2)将B(6,0)代入二次函数解析式中,求出二次函数解析式即可求出点C的坐标,然后利用待定系数法求出直线BC的解析式,根据一次函数的性质设出直线MN的解析式,然后联立方程结合一元二次方程根与系数的关系即可得出结论.
【详解】(1)①由题意,
解得,
∴二次函数的解析式为y=x2﹣8x+12.
②如图1中,设M(m,m2﹣8m+12),
∵B(6,0),C(0,12),
∴直线BC的解析式为y=﹣2x+12,
∵MQ⊥x轴,
∴Q(m,﹣2m+12),
∴QM=﹣2m+12﹣(m2﹣8m+12)=﹣m2+6m=﹣(m﹣3)2+9,
∵﹣1<0,
∴m=3时,QM有最大值,最大值为9.
(2)结论:m+n的值为定值.
理由:如图2中,
将B(6,0)代入二次函数解析式中,得
解得:
∴二次函数解析式为
∴C(0,﹣36﹣6b),
设直线BC的解析式为y=kx﹣36﹣6b,
把(6,0)代入得到:k=6+b,
∴直线BC的解析式为y=(6+b)x﹣36﹣6b,
∵MN∥CB,
∴可以假设直线MN的解析式为y=(6+b)x+b′,
由,消去y得到:x2﹣6x﹣36﹣6b﹣b′=0,
∴x1+x2=6,
∵点M、N的横坐标为m、n,
∴m+n=6.
∴m+n为定值,m+n=6.
【点睛】此题考查的是二次函数与一次函数的综合题型,掌握利用待定系数法求二次函数解析式、一次函数解析式、利用二次函数求最值、一元二次方程根与系数的关系是解决此题的关键.
25.(1)∠AEC=30 ;(2)不变,见解析;(3)3
【分析】(1)由AB=AC=2,∠BAC=120°,可得∠ABC=∠ACB,由∠BCE=∠BAD,可得∠AEC=30°;
(2)作△ABC的外接圆,延长AD交圆于E,则点E满足条件:∠BCE=∠BAD,可知在点D运动时,弧不变,利用同弧所对圆周角相等可得∠ACB=∠AEB=30°即可;
(3)过A作AF⊥BC,交⊙O于G,连结EG,BG,根据垂径定理可得AG为⊙O的直径,由AB=2,∠ABF=30°,可求AF,∠BGA=∠ABF=30°,可得AG=2AB=4,可证△ADF∽△AGE,可得,当最小时,AD=AF==1,即可.
【详解】解:(1)∵AB=AC=2,∠BAC=120°,
∴∠ABC=∠ACB=,
∵∠BCE=∠BAD,
∴∠AEC==30°
(2)作△ABC的外接圆,延长AD交圆于E,连结CE,则点E满足条件:∠BCE=∠BAD
∵在点D运动时,弧不变,
∴∠ACB=∠AEB=30°
∠AEB的度数不变化,∠AEB=30°
(3)过A作AF⊥BC,交⊙O于G,连结EG,BG,
∵AB=AC,
∴,
∴AG为⊙O的直径,
∵AB=2,∠ABF=30°,
∴AF=,
∵,
∴∠BGA=∠ABF=30°,
∴AG=2AB=4,
∵AG为⊙O的直径,
∴∠AEG=90°=∠AFD,
又∠DAF=∠GAE,
∴△ADF∽△AGE,
∴,即,
∴,
∴当最小时,AD=AF==1,
∴,
∴当a=1时,ab的最大值为3.
【点睛】本题考查等腰三角形性质,三角形内角和,三角形外接圆,圆周角性质,30°角直角三角形性质,三角形相似判定与性质,掌握等腰三角形性质,三角形内角和,三角形外接圆,圆周角性质,30°角直角三角形性质,三角形相似判定与性质是解题关键.
一、单选题
1.下列四个数:,,,中,绝对值最大的数是( ).
A. B. C. D.
2.电影《长津湖》备受观众喜爱,截止到2021年12月初,累计票房57.44亿元,57.44亿元用科学记数法表示为( )
A. B. C. D.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
4.下列四个命题中,真命题有( )
①一个三角形中至少有两个锐角. ②如果是的对顶角,那么.
③如果a为实数,那么. ④实数与数轴上的点是一一对应的.
⑤0.3,0.4,0.5是一组勾股数.
A.1个 B.2个 C.3个 D.4个
5.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心.若,则这个正多边形的边数为( )
A.7 B.8 C.9 D.10
6.在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )
A. B. C.D.
7.八(1)班15位同学每周体育锻炼时间情况如下表,则体育锻炼时间的中位数是( )
时间() 5 6 7 8
人数(人) 2 6 5 2
A. B. C. D.
8.下列运算正确的是( )
A. B. C. D.
9.红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是( )
A.红红不是胜就是输,所以红红胜的概率为
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
D.娜娜胜的概率和两人出相同手势的概率一样
10.下列命题正确的是().
A.任何事件发生的概率为1
B.随机事件发生的概率可以是任意实数
C.可能性很小的事件在一次实验中有可能发生
D.不可能事件在一次实验中也可能发生
二、填空题
11.在实数范围内因式分解: .
12.如图,在中,对角线,相交于点,点,分别是,的中点,若,则的长是 .
13.若关于x的一元二次方程ax2+bx﹣7=0的一个根是x=1,则2028﹣a﹣b= .
14.在△ABC中,∠ACB=90°,∠CAB=60°,AD是角平分线,CD=3cm,点P在边AB上运动(不与端点A,B重合),则线段DP的长度范围为 .
15.某校为了举办“庆祝建党90周年”的活动,调查了本校所有学生,调查的结果如图所示,根据图中给出的信息这所学校一共有 人.
16.如图,在以点为圆心的两个同心圆中,大圆的弦切小圆于点,若,则圆环的面积是 .
三、解答题
17.先化简,再求值:已知,求的值.
18.计算.(﹣)﹣2+(π﹣3)0﹣ ;
19.如图,已知锐角,.
(1)尺规作图:求作的角平分线;(保留作图痕迹,不写作法)
(2)点在边上且,请连接,求证:.
20.
(1)如图1,在中,,,求的面积;
(2)我市将在春天举办花展,政府为花展划定了一个三角形区域,米,米.根据需要,政府将花展区域内的区域划定为管理区域,禁止游客进入.其中点D,E分别在,边上,米,米.主办方在四边形内部摆满鲜花,其中在边上摆满郁金香.某游客想要拍摄AD边上的郁金香,且已知拍摄的张角等于时,拍照效果最佳.请你帮该游客在四边形的边上寻找最佳拍摄地点P,并求此时的长度.()
21.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是___;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是___;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
22.列方程解应用题
学校给七年级学生组织知识竞赛,共设20道题,各题的分值相同,每题必答.下表记录了5名学生的得分情况
参赛者 答对题数 答错题数 得分
小明 10 10 40
小红 19 1 94
小刚 20 0 100
小强 18 2 88
小丽 14 6 64
(1)参赛者小芳得76分,她答对了几道题?
(2)参赛者小花说她得了83分,你认为可能吗?为什么?
23.在△ABC中,D为BC边中点,DM,ND分别是∠ADB,∠ADC的内角平分线.
(1)请比较MN与BM+CN的大小关系,并证明;
(2)当∠BAC=90°时,BM=2,CN=,求MN的长度.
24.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A、B,与y轴相交于点C,B点的坐标为(6,0),点M为抛物线上的一个动点.
(1)若该二次函数图象的对称轴为直线x=4时:
①求二次函数的表达式;
②当点M位于x轴下方抛物线图象上时,过点M作x轴的垂线,交BC于点Q,求线段MQ的最大值;
(2)过点M作BC的平行线,交抛物线于点N,设点M、N的横坐标为m、n.在点M运动的过程中,试问m+n的值是否会发生改变?若改变,请说明理由;若不变,请求出m+n的值.
25.如图,在△ABC中,AB=AC=2,∠BAC=120°,点D为BC上一动点(不与B、C重合),E是AD延长线上的一点,且∠BCE=∠BAD.
(1)求∠AEC的度数;
(2)试说明:在点D运动的过程中,∠AEB的度数是一个定值;
(3)若AD=a,DE=b,求ab的最大值.
参考答案
1.A
【分析】先求出负数的绝对值的大小,再进行实数的比较即可.
【详解】∵,,,.
∴.
∴绝对值最大的数为-4.
故选A.
【点睛】本题考查实数大小的比较方法以及绝对值的性质.掌握“正数的绝对值是它本身,负数的绝对值是它的相反数”是解答本题的关键.
2.C
【分析】科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【详解】解:57.44亿用科学记数法表示为,故C正确.
故选:C.
【点睛】本题考查用科学记数法表示较大的数,一般形式为,其中,n可以用整数位数减去1来确定.用科学记数法表示数,一定要注意a的形式,以及指数n的确定方法.
3.B
【分析】根据轴对称图形和中心对称图形的定义,即可进行解答;轴对称图形:沿对称轴折叠后两部分可重合的图形;中心对称图形:绕旋转中心旋转180度后与原图重合的图形.
【详解】解:A.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
B.原图既是轴对称图形,又是中心对称图形,故此选项符合题意;
C.原图既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:B.
【点睛】此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.C
【分析】根据三角形内角的性质、对顶角的定义、绝对值的性质、数轴的定义、勾股数的定义进行判断即可.
【详解】解:①一个三角形中至少有两个锐角,正确,为真命题;
②如果是的对顶角,那么,正确,为真命题;
③当时,,故③错误,为假命题;
④实数与数轴上的点是一一对应的,正确,为真命题;
⑤勾股数需为正整数,故⑤错误,为假命题;
故选:C.
【点睛】本题考查了命题与定理的知识,熟练掌握勾股数的定义、数轴的定义、绝对值的性质及对顶角的定义和三角形内角的性质是解题的关键.
5.C
【分析】连接,,根据圆周角定理得到,进一步即可得到结论.
【详解】解:连接,,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,为半径的同一个圆上,
∵,
∴,
∴这个正多边形的边数,
故选:C.
【点睛】本题考查了正多边形与圆,圆周角定理,正确地理解题意是解题的关键.
6.C
【分析】根据正比例函数与一次函数的图象性质作答.
【详解】解:当k>2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,3象限;
当0<k<2时,正比例函数y=kx图象经过1,3象限,一次函数y=(k﹣2)x+k的图象1,2,4象限;
当k<0时,正比例函数y=kx图象经过2,4象限,一次函数y=(k﹣2)x+k的图象2,3,4象限,当(k﹣2)x+k=kx时,x=<0,所以两函数交点的横坐标小于0.
故选C.
【点睛】本题考查一次函数的图象性质,正比例函数的图象性质,关键是由k的取值确定函数所在的象限.
7.B
【分析】根据中位数的定义进行解答即可.
【详解】解:∵共有15个数,最中间的数是8个数,
∴这15名同学一周在校参加体育锻炼时间的中位数是6;
故选:B.
【点睛】此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
8.C
【分析】根据合并同类项法则,同底数幂的乘法,幂的乘方,积的乘方运算逐项计算排除即可.
【详解】、与不是同类项,不可以合并,此选项计算错误,不符合题意;
、,此选项计算错误,不符合题意;
、,此选项计算正确,符合题意;
、,此选项计算错误,不符合题意;
故选:.
【点睛】此题考查了整式的运算,解题的关键是熟练掌握合并同类项法则,同底数幂的乘法,幂的乘方,积的乘方运算及其应用.
9.A
【详解】试题解析:红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
红红娜娜 锤子 剪刀 布
锤子 (锤子,锤子) (锤子,剪刀) (锤子,布)
剪刀 (剪刀,锤子) (剪刀,剪刀) (剪刀,布)
布 (布,锤子) (布,剪刀) (布,布)
由表格可知,共有9种等可能情况.其中平局的有3种:(锤子,锤子)、(剪刀,剪刀)、(布,布).
因此,红红和娜娜两人出相同手势的概率为,两人获胜的概率都为,
红红不是胜就是输,所以红红胜的概率为,错误,故选项A符合题意,
故选项B,C,D不合题意;
故选A.
10.C
【分析】根据随机事件、不可能事件的定义和概率的性质判断各选项即可.
【详解】A中,只有必然事件概率才是1,错误;
B中,随机事件的概率p取值范围为:0<p<1,错误;
C中,可能性很小的事件,是有可能发生的,正确;
D中,不可能事件一定不发生,错误
故选:C
【点睛】本题考查事件的可能性,注意,任何事件的概率P一定在0至1之间.
11.
【分析】利用提公因式法和平方差公式即可解答.
【详解】
故答案为:.
【点睛】此题主要考查了实属范围内分解因式,采用提公因式法和平方差公式是解答本题的关键.
12.8
【分析】首先根据平行四边形的性质得出,再说明EF是△ADO的中位线,得出,即可求得答案.
【详解】∵四边形ABCD为平行四边形,
∴,
又∵E,F为AD,OD的中点,
∴,
∴,
∴,
故填:8.
【点睛】本题考查平行四边形的性质,三角形的中位线的判定和性质,熟练掌握平行四边形和三角形中位线的性质是解题关键.
13.2021
【分析】根据一元二次方程的解的定义,把x=1代入方程得到a+b﹣7=0,于是得a+b的值,再代入计算2028﹣a﹣b的值.
【详解】解:把x=1代入ax2+bx﹣7=0得a+b﹣7=0,
∴a+b=7
∴2028﹣a﹣b=2028-(a+b)=2021.
故答案为:2021.
【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
14.3≤DP<6
【分析】根据角平分线的定义得到∠CAD=∠BAD=30°,根据直角三角形的性质得到AD=2CD=6,过D作DP⊥AB于P,PD=AD=3,于是得到结论.
【详解】解:如图,
∵∠CAB=60°,AD是角平分线,
∴∠CAD=∠BAD=30°,
∵∠ACB=90°,CD=3,
∴AD=2CD=6,
过D作DP⊥AB于P,
∴∠APD=90°,
∴PD=AD=3,
∴线段DP的长度范围为3≤DP<6,
故答案为:3≤DP<6.
【点睛】本题考查了含30°角的直角三角形的性质、角平分线的定义,正确的作出辅助线是解题的关键.
15.400
【分析】根据A文艺演出的人数及所占的比例即可得出总人数,
【详解】解:160÷40%=400(人).
则这所学校一共有400人
故答案为:400.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
16.
【分析】如图,连接、,设,,由切线的性质得,,由垂径定理得,,由勾股定理得,,由即可求出圆环的面积.
【详解】
如图,连接、,设,,
大圆的弦切小圆于点,
,
,
,
在中,,
,,
,
故答案为:.
【点睛】本题考查了切线的性质、垂径定理、勾股定理以及圆与圆环的面积计算,掌握圆的相关知识是解题的关键.
17.,.
【分析】先去括号,再合并同类项,然后整体代入求值即可.
【详解】解:
=
=.
当时,
原式=
=
【点睛】本题考查了整式的化简求值,解题关键是熟练运用整式加减法则进行化简,整体代入求值.
18.7
【分析】根据负整数指数幂、零指数幂和二次根式的乘法可以解答本题.
【详解】解:(﹣)﹣2+(π﹣3)0﹣
=9+1﹣
=9+1﹣3
=7
【点睛】本题主要考查实数的混合运算,掌握负整数指数幂、零指数幂和二次根式的乘法的运算法则是关键.
19.(1)见解析;(2)见解析
【分析】(1)以点B为圆心,任意长为半径画弧与AB、BC相交,再分别以两个交点为圆心,大于两点间距离的一半为半径,在角的内部相交于一点,连接此点与点B并延长交AC与点D;
(2)根据已知条件证明△DBE≌△DBC,即可得到结论.
【详解】(1)作图如图所示,
(2)证明:∵平分,
∴,
又∵,,
∴,
∴.
【点睛】此题考查了基本作图--角平分线的画法,以及三角形全等的判定及性质.解题关键是掌握基本作图.
20.(1)
(2)取点见解析,100或
【分析】对于(1),先说明是等边三角形,再根据勾股定理求出高,根据三角形的面积计算即可;
对于(2),当点P在上时,根据“两角分别相等的三角形相似”得,再根据相似三角形的对应边长比例得,然后代入数值得出答案;当点P在上时,利用平行线分线段成比例定理得到,即,解方程即可.
【详解】(1)∵,,
∴是等边三角形,
∴.
过点A作,于点F,
∴.
根据勾股定理,得.
∴;
(2)解:如图所示,当点P在上时,
∵,
∴.
∵,,
∴,
∴,
∴,
即,
解得或,
当时,,不符合题意;
∴米;
当点P在上时,
∵,
∴,
∴,即,
∴米,
综上所述,的长为100米或米
【点睛】本题主要考查了等边三角形的性质和判定,等腰三角形的性质,相似三角形的性质和判定,灵活选择判定定理是解题的关键.
21.(1)0
(2)
(3)4个
【详解】(1)解:∵口袋中装有4个白球和6个红球,
∴从口袋中随机摸出一个球是绿球是不可能事件,
发生的概率为0;
故答案为:0;
(2)解:∵口袋中装有4个白球和6个红球,共有10个球,
∴从口袋中随机摸出一个球是红球的概率是=;
故答案为:;
(3)解:设取走了x个红球,根据题意得:
,
解得:x=4,
答:取走了4个红球.
【点睛】此题考查了用概率公式求事件概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
22.(1)小芳答对了16道题;(2)小花不可能的83分,理由见解析.
【分析】根据表格得出答对一题得5分,再算出错一题扣1分,
(1)设小芳答对了m道题,答错了(20-m)道题,根据答对的得分+加上答错的得分=76分建立方程求出其解即可;
(2)假设小花得83分可能,设答对了y道题,答错了(20-y)道题,根据答对的得分+加上答错的得分=83分建立方程求出其解即可.
【详解】由小刚可得答对一题得5分
设答错一题得x分,10x+50=40(或19×5+x=94或18×5+2x=88或14×5+6x=64)
x=-1
(1)设小芳答对了m道题,则答错(20-m)道题
5m-(20-m)=76
m=16
答小芳答对了16道题
(2)不可能.
假设可能,设小花答对了y道题,则答错了(20-y)道题
5y-(20-y)=83
y=
因为不是整数
所以假设不成立
所以小花不可能的83分
【点睛】本题考查了列一元一次方程解实际问题的运用,结论猜想试题的运用,解答时关键答对的得分+加上答错的得分=总得分是关键.
23.(1)BM+CN>MN,理由见解析;(2)3
【分析】(1)如图,延长ND到H,使ND=DH,连接MH,BH,由“SAS”可证△CDN≌△BDH,可得BH=CN,DH=DN,∠ACB=∠DBH,由线段垂直平分线的性质可得MN=MH,由三角形的三边关系可求解;
(2)先证明∠ABH=90°,在Rt△BHM中,由勾股定理可求MH的长,即可求解.
【详解】解:(1)BM+CN>MN,
理由如下:如图,延长ND到H,使ND=DH,连接MH,BH,
∵点D是BC的中点,
∴BD=CD,
在△CDN和△BDH中,
,
∴△CDN≌△BDH(SAS),
∴BH=CN,DH=DN,∠ACB=∠DBH,
∵DM,ND分别是∠ADB,∠ADC的内角平分线,
∴∠ADM=∠ADB,∠ADN=∠ADC,
∴∠ADM+∠ADN=90°,
∴∠MDN=90°,
∴MH=MN,
在△BMH中,BM+BH>MH,
∴BM+CN>MN;
(2)∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
∴∠ABC+∠DBH=90°,
∴∠HBM=90°,
∵BM=2,BH=CN=,
∴MH==3,
∴MN=MH=3.
【点睛】本题考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,添加恰当辅助线构造全等三角形是解题的关键.
24.(1)①y=x2﹣8x+12;②线段MQ的最大值为9.(2)m+n的值为定值.m+n=6.
【分析】(1)①根据点B的坐标和二次函数图象的对称轴即可求出二次函数解析式;
②设M(m,m2﹣8m+12),利用待定系数法求出直线BC的解析式,从而求出Q(m,﹣2m+12),即可求出MQ的长与m的函数关系式,然后利用二次函数求最值即可;
(2)将B(6,0)代入二次函数解析式中,求出二次函数解析式即可求出点C的坐标,然后利用待定系数法求出直线BC的解析式,根据一次函数的性质设出直线MN的解析式,然后联立方程结合一元二次方程根与系数的关系即可得出结论.
【详解】(1)①由题意,
解得,
∴二次函数的解析式为y=x2﹣8x+12.
②如图1中,设M(m,m2﹣8m+12),
∵B(6,0),C(0,12),
∴直线BC的解析式为y=﹣2x+12,
∵MQ⊥x轴,
∴Q(m,﹣2m+12),
∴QM=﹣2m+12﹣(m2﹣8m+12)=﹣m2+6m=﹣(m﹣3)2+9,
∵﹣1<0,
∴m=3时,QM有最大值,最大值为9.
(2)结论:m+n的值为定值.
理由:如图2中,
将B(6,0)代入二次函数解析式中,得
解得:
∴二次函数解析式为
∴C(0,﹣36﹣6b),
设直线BC的解析式为y=kx﹣36﹣6b,
把(6,0)代入得到:k=6+b,
∴直线BC的解析式为y=(6+b)x﹣36﹣6b,
∵MN∥CB,
∴可以假设直线MN的解析式为y=(6+b)x+b′,
由,消去y得到:x2﹣6x﹣36﹣6b﹣b′=0,
∴x1+x2=6,
∵点M、N的横坐标为m、n,
∴m+n=6.
∴m+n为定值,m+n=6.
【点睛】此题考查的是二次函数与一次函数的综合题型,掌握利用待定系数法求二次函数解析式、一次函数解析式、利用二次函数求最值、一元二次方程根与系数的关系是解决此题的关键.
25.(1)∠AEC=30 ;(2)不变,见解析;(3)3
【分析】(1)由AB=AC=2,∠BAC=120°,可得∠ABC=∠ACB,由∠BCE=∠BAD,可得∠AEC=30°;
(2)作△ABC的外接圆,延长AD交圆于E,则点E满足条件:∠BCE=∠BAD,可知在点D运动时,弧不变,利用同弧所对圆周角相等可得∠ACB=∠AEB=30°即可;
(3)过A作AF⊥BC,交⊙O于G,连结EG,BG,根据垂径定理可得AG为⊙O的直径,由AB=2,∠ABF=30°,可求AF,∠BGA=∠ABF=30°,可得AG=2AB=4,可证△ADF∽△AGE,可得,当最小时,AD=AF==1,即可.
【详解】解:(1)∵AB=AC=2,∠BAC=120°,
∴∠ABC=∠ACB=,
∵∠BCE=∠BAD,
∴∠AEC==30°
(2)作△ABC的外接圆,延长AD交圆于E,连结CE,则点E满足条件:∠BCE=∠BAD
∵在点D运动时,弧不变,
∴∠ACB=∠AEB=30°
∠AEB的度数不变化,∠AEB=30°
(3)过A作AF⊥BC,交⊙O于G,连结EG,BG,
∵AB=AC,
∴,
∴AG为⊙O的直径,
∵AB=2,∠ABF=30°,
∴AF=,
∵,
∴∠BGA=∠ABF=30°,
∴AG=2AB=4,
∵AG为⊙O的直径,
∴∠AEG=90°=∠AFD,
又∠DAF=∠GAE,
∴△ADF∽△AGE,
∴,即,
∴,
∴当最小时,AD=AF==1,
∴,
∴当a=1时,ab的最大值为3.
【点睛】本题考查等腰三角形性质,三角形内角和,三角形外接圆,圆周角性质,30°角直角三角形性质,三角形相似判定与性质,掌握等腰三角形性质,三角形内角和,三角形外接圆,圆周角性质,30°角直角三角形性质,三角形相似判定与性质是解题关键.
同课章节目录
