浙江省湖州市2023-2024学年高一上学期期末调研测试数学试题(含答案)
文档属性
| 名称 | 浙江省湖州市2023-2024学年高一上学期期末调研测试数学试题(含答案) | 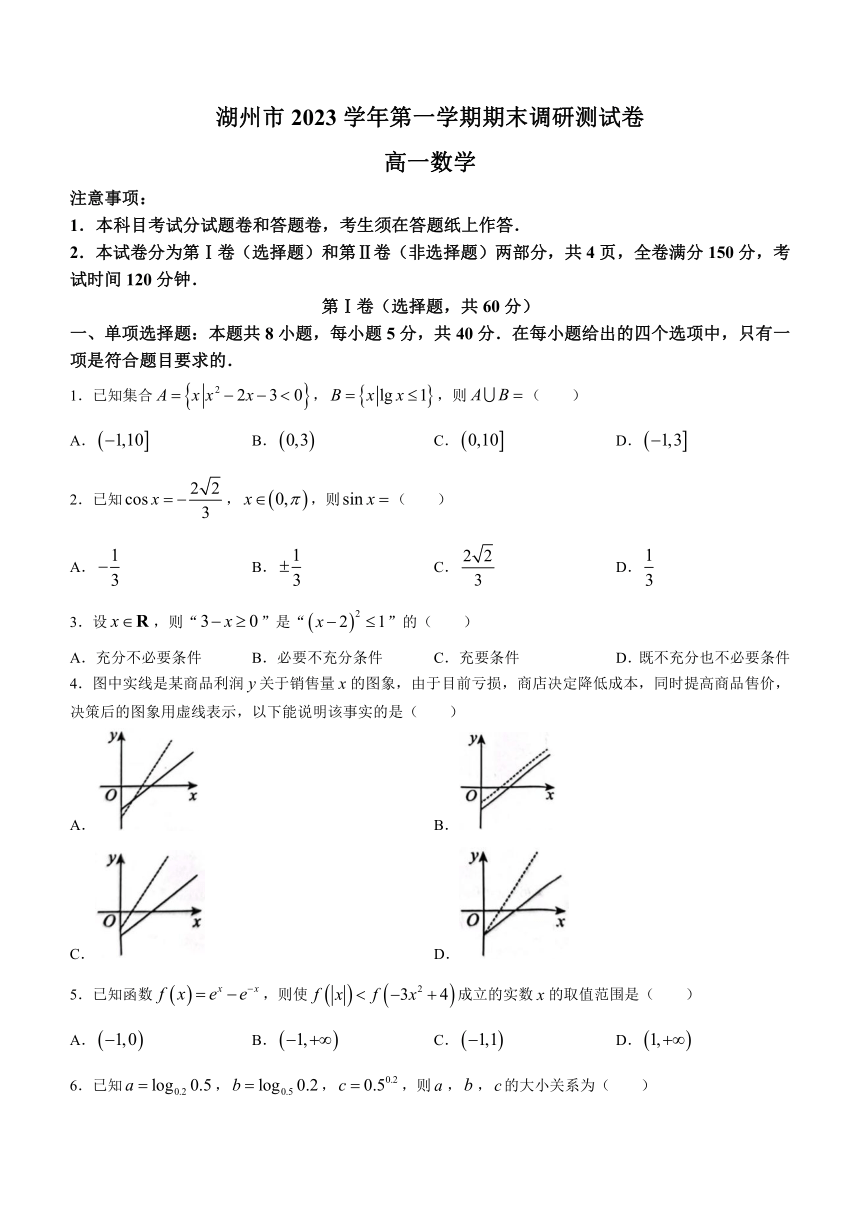 | |
| 格式 | docx | ||
| 文件大小 | 708.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 22:20:01 | ||
图片预览





文档简介
湖州市2023学年第一学期期末调研测试卷
高一数学
注意事项:
1.本科目考试分试题卷和答题卷,考生须在答题纸上作答.
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.已知,,则( )
A. B. C. D.
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.图中实线是某商品利润关于销售量的图象,由于目前亏损,商店决定降低成本,同时提高商品售价,决策后的图象用虚线表示,以下能说明该事实的是( )
A. B.
C. D.
5.已知函数,则使成立的实数的取值范围是( )
A. B. C. D.
6.已知,,,则,,的大小关系为( )
A. B. C. D.
7.我们知道,每一个音都是由纯音合成的,纯音的数学模型是.已知某音是由3个不同的纯音合成,其函数为,则( )
A. B.的最大值为
C.的最小正周期为 D.在上是增函数
8.已知函数()的零点为,函数()的零点为,则下列结论错误的是( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.给出下列四个选项中,其中正确的选项有( )
A.若角的终边过点且,则
B.设角为锐角(单位为弧度),则
C.命题“,使得”的否定是:“,均有”
D.若,,则“”是“”的充分不必要条件
10.若,,,则下列命题正确的是( )
A.若且,则 B.若且,则
C.若,则 D.
11.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动5圈,如图,将该筒车抽象为圆,筒车上的盛水桶抽象为圆上的点,已知圆的半径为,圆心距离水面,且当圆上点从水中浮现时(图中点)开始计算时间,点的高度随时间(单位秒)变化时满足函数模型,则下列说法正确的是( )
A.函数的初相为 B.1秒时,函数的相位为0
C.4秒后,点第一次到达最高点 D.7秒和15秒时,点高度相同
12.已知函数对任意实数,都满足,且,则下列说法正确的是( )
A.是偶函数 B.
C. D.
第Ⅱ卷(非选择题部分,共90分)
注意事项:用钢笔或签字笔将试题卷中的题目做在答题纸上,做在试题卷上无效.
三、填空题:本题共4小题,每小题5分,共20分.
13.函数的反函数是______.
14.已知某扇形的圆心角是,半径是3,则该扇形的面积是______.
15.设函数,,则函数的值域是______.
16.已知,其中,且,若函数在区间上有且只有三个零点,则的范围为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知集合,.
(1)求和;
(2)若集合,且,求实数的取值范围.
18.(本题满分12分)
在平面直角坐标系中,角的始边为轴的非负半轴,终边过点.
(1)求的值;
(2)求的值.
19.(本题满分12分)
随着电动汽车研发技术的日益成熟,电动汽车的普及率越来越高.某型号电动汽车在封闭路段进行测试,限速(不含).经多次测试得到,该汽车每小时耗电量(单位:)与速度(单位:)的数据如下表所示.
0 10 30 70
0 1325 3375 9275
为了描述国道上该汽车每小时耗电量与速度的关系,现有以下三种函数模型供选择:
,,.
(1)当时,请选出你认为最符合表格所列数据实际的函数模型,并求出相应的函数解析式;
(2)在本次测试报告中,该电动汽车的最长续航里程为.若测试过程为匀速运动,请计算本次测试时的车速为何值时,该电动汽车电池所需的容量(单位:)最小?并计算出该最小值.
20.(本题满分12分)
已知定义域为的函数是奇函数.
(1)判断函数的单调性,并证明;
(2)解关于的不等式.
21.(本题满分12分)
2023年12月1日,“民族魂·中国梦——阳光下成长”2023年浙江省中小学生艺术节闭幕式暨颁奖晚会在湖州大剧院举行.为迎接艺术节闭幕式的到来,承办方计划将场地内一处扇形荒地进行改造.已知该扇形荒地的半径为20米,圆心角,承办方初步计划将其中的(如下左图,点位于弧上,,分别位于半径,)区域改造为花卉区,扇形荒地内其余区域改造为草坪区.
(1)承办方进一步计划将,设计为观光步道,其宽度忽略不计.若观光步道造价为元/米,请你设计观光步道的造价预算,确保观光步道最长时仍有资金保障;
(2)因某种原因,承办方修改了最初的改造计划,将花卉区设计为矩形(如下右图,其中,位于半径上,位于半径上).为美观起见,承办方最后决定将四边形设计为正方形.求此时花卉区的面积.
22.(本题满分12分)
已知函数满足,函数.
(1)求函数的解析式;
(2)若不等式在上恒成立,求实数的取值范围;
(3)若关于的方程有四个不同的实数解,求实数的取值范围.
湖州市2023学年第一学期高一期末教学测试
数学参考答案
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 A D B C C A D B
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.
题号 9 10 11 12
答案 ABD BD BC ACD
三、填空题:本大题共4小题,每小题5分,共20分.
13. 14. 15. 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
解析:(1),,
;,
(2)若,且,则,
所以,解得,的取值范围.
18.(本题满分12分)
解析:(1)由题意得,,则;
另解:由角终边过点,得,,
则;
(2)由题意得,,,
,,
(其它解法也酌情给分)
19.(本题满分12分)
解析:(1)对于,当时,它无意义,所以不符合题意;
对于,它显然是个减函数,所以不符合题意;
故选.
根据提供的数据,有
当时,.
(2)设车速为,所用时间为,
所耗电量
要使得续航里程最长,则耗电量达到最小,即.
所以当测试员控制的车速为,
该电动汽车的电池所需的最小容量为.
20.(本题满分12分)
解析:(1)因为是定义在上的奇函数,则,
即
,解得,
所以,故在上是递减函数.
证明:任取,,且,
,,
,即,故是定义在上的递减函数;
(2),,
是上的减函数,,
21.(本题满分12分)
解析:(1)设,,过点做的垂线交于,
,,
,
所以预算应该设定为元.
(2),
22.(本题满分12分)
解析:(1)因为①
则②
故联立上述方程组,解得
(2)由(1)知,,
因为不等式在上恒成立,
所以在上恒成立,
设,则,
所以,,在上恒成立,
所以,在上恒成立,
因为,所以,当时,取得最大值,最大值为,
所以,,在上恒成立,则,
所以的取值范围是.
(3)方程等价于,
即,,
令,则方程化为,(),
因为方程有四个不同的实数解,
所以,(),有两个不同的正根、,
记,
所以,,此时.另解,,此时.
综上,.
高一数学
注意事项:
1.本科目考试分试题卷和答题卷,考生须在答题纸上作答.
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.已知,,则( )
A. B. C. D.
3.设,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.图中实线是某商品利润关于销售量的图象,由于目前亏损,商店决定降低成本,同时提高商品售价,决策后的图象用虚线表示,以下能说明该事实的是( )
A. B.
C. D.
5.已知函数,则使成立的实数的取值范围是( )
A. B. C. D.
6.已知,,,则,,的大小关系为( )
A. B. C. D.
7.我们知道,每一个音都是由纯音合成的,纯音的数学模型是.已知某音是由3个不同的纯音合成,其函数为,则( )
A. B.的最大值为
C.的最小正周期为 D.在上是增函数
8.已知函数()的零点为,函数()的零点为,则下列结论错误的是( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.给出下列四个选项中,其中正确的选项有( )
A.若角的终边过点且,则
B.设角为锐角(单位为弧度),则
C.命题“,使得”的否定是:“,均有”
D.若,,则“”是“”的充分不必要条件
10.若,,,则下列命题正确的是( )
A.若且,则 B.若且,则
C.若,则 D.
11.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,现有一个筒车按逆时针方向匀速转动.每分钟转动5圈,如图,将该筒车抽象为圆,筒车上的盛水桶抽象为圆上的点,已知圆的半径为,圆心距离水面,且当圆上点从水中浮现时(图中点)开始计算时间,点的高度随时间(单位秒)变化时满足函数模型,则下列说法正确的是( )
A.函数的初相为 B.1秒时,函数的相位为0
C.4秒后,点第一次到达最高点 D.7秒和15秒时,点高度相同
12.已知函数对任意实数,都满足,且,则下列说法正确的是( )
A.是偶函数 B.
C. D.
第Ⅱ卷(非选择题部分,共90分)
注意事项:用钢笔或签字笔将试题卷中的题目做在答题纸上,做在试题卷上无效.
三、填空题:本题共4小题,每小题5分,共20分.
13.函数的反函数是______.
14.已知某扇形的圆心角是,半径是3,则该扇形的面积是______.
15.设函数,,则函数的值域是______.
16.已知,其中,且,若函数在区间上有且只有三个零点,则的范围为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分)
已知集合,.
(1)求和;
(2)若集合,且,求实数的取值范围.
18.(本题满分12分)
在平面直角坐标系中,角的始边为轴的非负半轴,终边过点.
(1)求的值;
(2)求的值.
19.(本题满分12分)
随着电动汽车研发技术的日益成熟,电动汽车的普及率越来越高.某型号电动汽车在封闭路段进行测试,限速(不含).经多次测试得到,该汽车每小时耗电量(单位:)与速度(单位:)的数据如下表所示.
0 10 30 70
0 1325 3375 9275
为了描述国道上该汽车每小时耗电量与速度的关系,现有以下三种函数模型供选择:
,,.
(1)当时,请选出你认为最符合表格所列数据实际的函数模型,并求出相应的函数解析式;
(2)在本次测试报告中,该电动汽车的最长续航里程为.若测试过程为匀速运动,请计算本次测试时的车速为何值时,该电动汽车电池所需的容量(单位:)最小?并计算出该最小值.
20.(本题满分12分)
已知定义域为的函数是奇函数.
(1)判断函数的单调性,并证明;
(2)解关于的不等式.
21.(本题满分12分)
2023年12月1日,“民族魂·中国梦——阳光下成长”2023年浙江省中小学生艺术节闭幕式暨颁奖晚会在湖州大剧院举行.为迎接艺术节闭幕式的到来,承办方计划将场地内一处扇形荒地进行改造.已知该扇形荒地的半径为20米,圆心角,承办方初步计划将其中的(如下左图,点位于弧上,,分别位于半径,)区域改造为花卉区,扇形荒地内其余区域改造为草坪区.
(1)承办方进一步计划将,设计为观光步道,其宽度忽略不计.若观光步道造价为元/米,请你设计观光步道的造价预算,确保观光步道最长时仍有资金保障;
(2)因某种原因,承办方修改了最初的改造计划,将花卉区设计为矩形(如下右图,其中,位于半径上,位于半径上).为美观起见,承办方最后决定将四边形设计为正方形.求此时花卉区的面积.
22.(本题满分12分)
已知函数满足,函数.
(1)求函数的解析式;
(2)若不等式在上恒成立,求实数的取值范围;
(3)若关于的方程有四个不同的实数解,求实数的取值范围.
湖州市2023学年第一学期高一期末教学测试
数学参考答案
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 A D B C C A D B
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分.
题号 9 10 11 12
答案 ABD BD BC ACD
三、填空题:本大题共4小题,每小题5分,共20分.
13. 14. 15. 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
解析:(1),,
;,
(2)若,且,则,
所以,解得,的取值范围.
18.(本题满分12分)
解析:(1)由题意得,,则;
另解:由角终边过点,得,,
则;
(2)由题意得,,,
,,
(其它解法也酌情给分)
19.(本题满分12分)
解析:(1)对于,当时,它无意义,所以不符合题意;
对于,它显然是个减函数,所以不符合题意;
故选.
根据提供的数据,有
当时,.
(2)设车速为,所用时间为,
所耗电量
要使得续航里程最长,则耗电量达到最小,即.
所以当测试员控制的车速为,
该电动汽车的电池所需的最小容量为.
20.(本题满分12分)
解析:(1)因为是定义在上的奇函数,则,
即
,解得,
所以,故在上是递减函数.
证明:任取,,且,
,,
,即,故是定义在上的递减函数;
(2),,
是上的减函数,,
21.(本题满分12分)
解析:(1)设,,过点做的垂线交于,
,,
,
所以预算应该设定为元.
(2),
22.(本题满分12分)
解析:(1)因为①
则②
故联立上述方程组,解得
(2)由(1)知,,
因为不等式在上恒成立,
所以在上恒成立,
设,则,
所以,,在上恒成立,
所以,在上恒成立,
因为,所以,当时,取得最大值,最大值为,
所以,,在上恒成立,则,
所以的取值范围是.
(3)方程等价于,
即,,
令,则方程化为,(),
因为方程有四个不同的实数解,
所以,(),有两个不同的正根、,
记,
所以,,此时.另解,,此时.
综上,.
同课章节目录
