安徽省安庆市重点中学2023-2024学年九年级下学期开学考试数学试题(无答案)
文档属性
| 名称 | 安徽省安庆市重点中学2023-2024学年九年级下学期开学考试数学试题(无答案) | 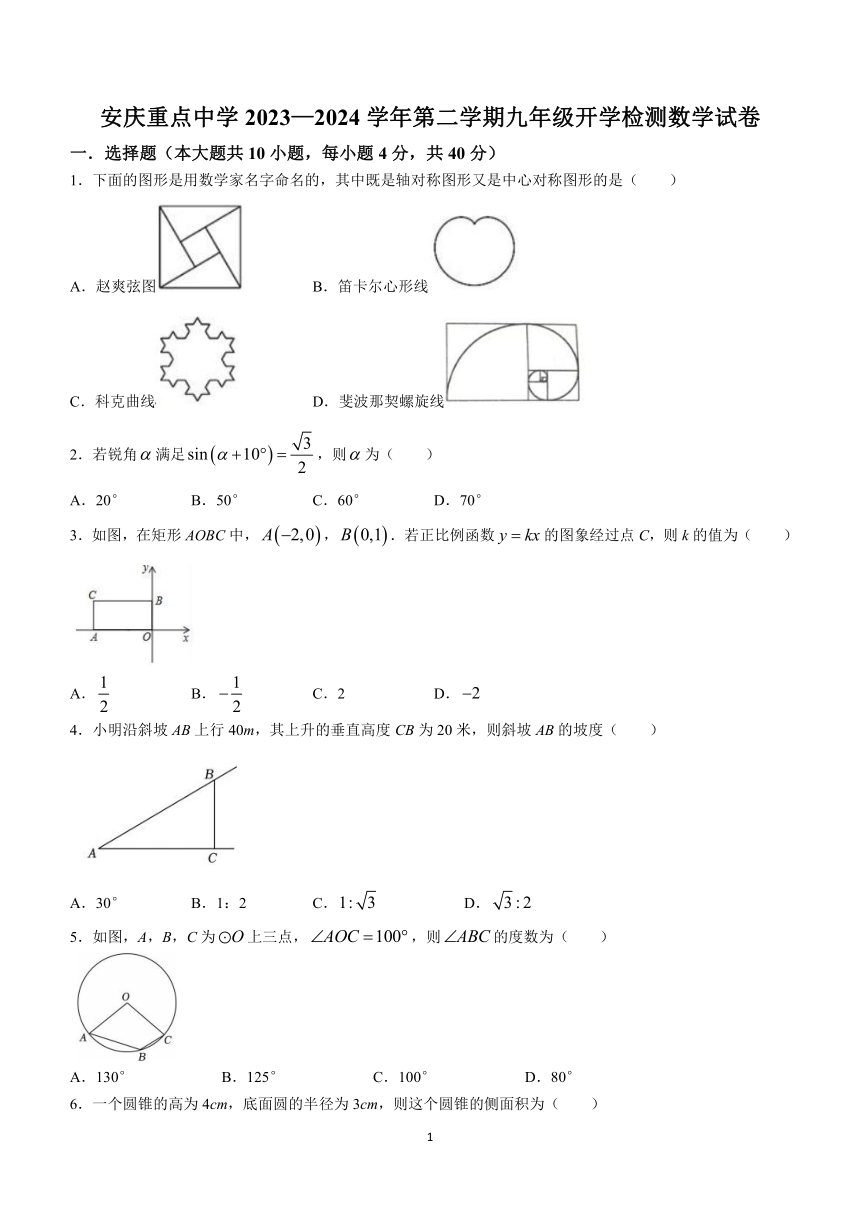 | |
| 格式 | doc | ||
| 文件大小 | 766.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 21:33:39 | ||
图片预览



文档简介
安庆重点中学2023—2024学年第二学期九年级开学检测数学试卷
一.选择题(本大题共10小题,每小题4分,共40分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图 B.笛卡尔心形线
C.科克曲线 D.斐波那契螺旋线
2.若锐角满足,则为( )
A.20° B.50° C.60° D.70°
3.如图,在矩形AOBC中,,.若正比例函数的图象经过点C,则k的值为( )
A. B. C.2 D.
4.小明沿斜坡AB上行40m,其上升的垂直高度CB为20米,则斜坡AB的坡度( )
A.30° B.1:2 C. D.
5.如图,A,B,C为上三点,,则的度数为( )
A.130° B.125° C.100° D.80°
6.一个圆锥的高为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为( )
A. B. C. D.
7.如图,在中,,,点D是AC上一点,连接BD.若,,则BD的长为( )
A. B. C.3 D.
8.如图,在中E是AC上的一点,,点D是BC的中点,连接AD、BE交于点F,若的面积为36,则四边形CDFE的面积是( )
A.7 B.6 C. D.
9.已知二次函数,当时,y有最小值为3,则实数k的值为( )
A.0 B.或0 C.或0 D.或0或
10.如图,在中,,CD是高,AE是角平分线,BF是中线,AE与CD交于点M,AE与BF交于点N,下面说法正确的有( )
①;②;③;④若,,则.
A.①②③ B.①②④ C.①③④ D.①②③④
二.填空题(本大题共4小题,每小题5分,共20分)
11.如果二次函数的顶点在x轴上,那么______.
12.如图,小明在某天15:00时测量某树的影长时,日照的光线与地面的夹角,当他在17:00时测量该树的影长时,日照的光线与地面的夹角,若两次测得的影长之差CD长为m,则树的高度为______m.
13.如图,在扇形AOB中,,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为______.
14.在中,,AD是的角平分线,BI平分∠CBA交AD于I.
问:
(1)______;
(2)若,,则______.
三.解答题(本大题共4小题,每小题8分,共32分)
15.计算:
16.在边长为1的正方形网格中如图所示.
(1)以点C为位似中心,作出的位似图形,使原图形与新图形位似比为1:2.且位于点C的异侧,并表示出的坐标.
(2)作出绕点O顺时针旋转90°后的图形,并表示出的坐标.
17.如图,一次函数与反比例函数的图象交于点,,与x轴交于点D,与y轴交于点C.
(1)求m,n的值;
(2)观察函数图象,直接写出不等式的解集:______.
18.已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:;
(2)如果,,求菱形ABCD的边长.
四.解答题(本大题共2小题,每小题10分,共20分)
19.阅读材料并解答问题:
与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,…,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n()边形的面积为,其内切圆的半径为r,试探索正n边形的面积
图① 图② 图③ 图④
(1)如图1,当时,设AB切圆O于点C,连接OC,OA,OB,∴,,∴,.
在中,∵,,∴,,∴,∴.
(2)如图2,当时,仿照(1)中的方法和过程可求得:______;
(3)如图3,当时,仿照(1)中的方法和过程求;
(4)如图4,根据以上探索过程,请直接写出______.
20.一款学习桌的桌面宽度AB为60厘米,书写时桌面适宜倾斜角()为20°.若书桌如图放置,则桌沿(点A)处,应与竖直的填壁至少相距多少厘米,才能保证书桌桌面可以调整放平?(结果保留一位小数。参考数据:,,)
五.(本题12分)
21.如图,在中,,BD是角平分线,以点D为圆心,DA为半径的与AC相交于点E
(1)求证:BC是的切线;
(2)若,,求CE的长.
六.(本题12分)
22.已知抛物线K:关于直线对称,且经过点.
(1)求抛物线K的函数表达式;
(2)若抛物线K与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.求A、B、C三点的坐标,并求的面积;
(3)将抛物线K向左或向右平移,得到抛物线,且与x轴相交于、两点(点在点的左侧),并与y轴相交于点,要使和的面积相等,求所有满足条件的抛物线的函数表达式.
七.(本题14分)
23.如图①,平行四边形ABCD中,,于点E,交AD的延长线于点F.
(1)求证:;
(2)连接BF,分别交CE、CD于G、H(如图②),求证:;
(3)在图②中,若,求.
图① 图②
一.选择题(本大题共10小题,每小题4分,共40分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A.赵爽弦图 B.笛卡尔心形线
C.科克曲线 D.斐波那契螺旋线
2.若锐角满足,则为( )
A.20° B.50° C.60° D.70°
3.如图,在矩形AOBC中,,.若正比例函数的图象经过点C,则k的值为( )
A. B. C.2 D.
4.小明沿斜坡AB上行40m,其上升的垂直高度CB为20米,则斜坡AB的坡度( )
A.30° B.1:2 C. D.
5.如图,A,B,C为上三点,,则的度数为( )
A.130° B.125° C.100° D.80°
6.一个圆锥的高为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为( )
A. B. C. D.
7.如图,在中,,,点D是AC上一点,连接BD.若,,则BD的长为( )
A. B. C.3 D.
8.如图,在中E是AC上的一点,,点D是BC的中点,连接AD、BE交于点F,若的面积为36,则四边形CDFE的面积是( )
A.7 B.6 C. D.
9.已知二次函数,当时,y有最小值为3,则实数k的值为( )
A.0 B.或0 C.或0 D.或0或
10.如图,在中,,CD是高,AE是角平分线,BF是中线,AE与CD交于点M,AE与BF交于点N,下面说法正确的有( )
①;②;③;④若,,则.
A.①②③ B.①②④ C.①③④ D.①②③④
二.填空题(本大题共4小题,每小题5分,共20分)
11.如果二次函数的顶点在x轴上,那么______.
12.如图,小明在某天15:00时测量某树的影长时,日照的光线与地面的夹角,当他在17:00时测量该树的影长时,日照的光线与地面的夹角,若两次测得的影长之差CD长为m,则树的高度为______m.
13.如图,在扇形AOB中,,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为______.
14.在中,,AD是的角平分线,BI平分∠CBA交AD于I.
问:
(1)______;
(2)若,,则______.
三.解答题(本大题共4小题,每小题8分,共32分)
15.计算:
16.在边长为1的正方形网格中如图所示.
(1)以点C为位似中心,作出的位似图形,使原图形与新图形位似比为1:2.且位于点C的异侧,并表示出的坐标.
(2)作出绕点O顺时针旋转90°后的图形,并表示出的坐标.
17.如图,一次函数与反比例函数的图象交于点,,与x轴交于点D,与y轴交于点C.
(1)求m,n的值;
(2)观察函数图象,直接写出不等式的解集:______.
18.已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)求证:;
(2)如果,,求菱形ABCD的边长.
四.解答题(本大题共2小题,每小题10分,共20分)
19.阅读材料并解答问题:
与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,…,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n()边形的面积为,其内切圆的半径为r,试探索正n边形的面积
图① 图② 图③ 图④
(1)如图1,当时,设AB切圆O于点C,连接OC,OA,OB,∴,,∴,.
在中,∵,,∴,,∴,∴.
(2)如图2,当时,仿照(1)中的方法和过程可求得:______;
(3)如图3,当时,仿照(1)中的方法和过程求;
(4)如图4,根据以上探索过程,请直接写出______.
20.一款学习桌的桌面宽度AB为60厘米,书写时桌面适宜倾斜角()为20°.若书桌如图放置,则桌沿(点A)处,应与竖直的填壁至少相距多少厘米,才能保证书桌桌面可以调整放平?(结果保留一位小数。参考数据:,,)
五.(本题12分)
21.如图,在中,,BD是角平分线,以点D为圆心,DA为半径的与AC相交于点E
(1)求证:BC是的切线;
(2)若,,求CE的长.
六.(本题12分)
22.已知抛物线K:关于直线对称,且经过点.
(1)求抛物线K的函数表达式;
(2)若抛物线K与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.求A、B、C三点的坐标,并求的面积;
(3)将抛物线K向左或向右平移,得到抛物线,且与x轴相交于、两点(点在点的左侧),并与y轴相交于点,要使和的面积相等,求所有满足条件的抛物线的函数表达式.
七.(本题14分)
23.如图①,平行四边形ABCD中,,于点E,交AD的延长线于点F.
(1)求证:;
(2)连接BF,分别交CE、CD于G、H(如图②),求证:;
(3)在图②中,若,求.
图① 图②
同课章节目录
