18.2 勾股定理的逆定理
文档属性
| 名称 | 18.2 勾股定理的逆定理 |  | |
| 格式 | rar | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-07 21:25:00 | ||
图片预览



文档简介
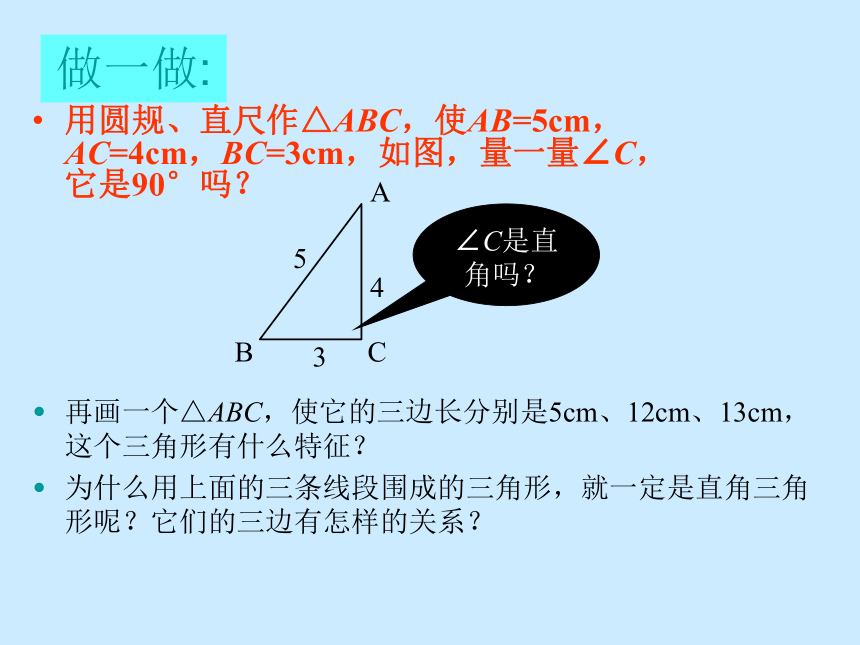
课件11张PPT。18.2 勾股定理的逆定理据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图。这样围成的三角形中,最长边所对的角就是直角。知道为什么吗?这节课我们一起来探讨这个问题,相信同学们会感兴趣的.做一做:用圆规、直尺作△ABC,使AB=5cm,AC=4cm,BC=3cm,如图,量一量∠C,它是90°吗?∠C是直角吗?再画一个△ABC,使它的三边长分别是5cm、12cm、13cm,这个三角形有什么特征?
为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?猜想: 如果一个三角形的三边长a、b、c满足下面的关系a2+b2=c2,那么这个三角形是直角三角形吗? 证明 作△A’B’C’,使∠C’=90°,
A’C’=b,B’C’=a,如图(2),
那么A’B’2=a2+b2.(勾股定理)
又∵a2+b2=c2,(已知)
∴A’B’2=c2,A’B’=c (A’B’>0)
在ABC和A’B’C’中,
∵BC=a=B’C’,
CA=b=C’A’,
AB=c=A’B’,
∴△ABC≌△A’B’C’(SSS) ∴∠C=∠C’=90°,
∴△ABC是直角三角形.已知:在△ABC中,AB=c,BC=a,AC=b,并且a2+b2=c2,如图(1).
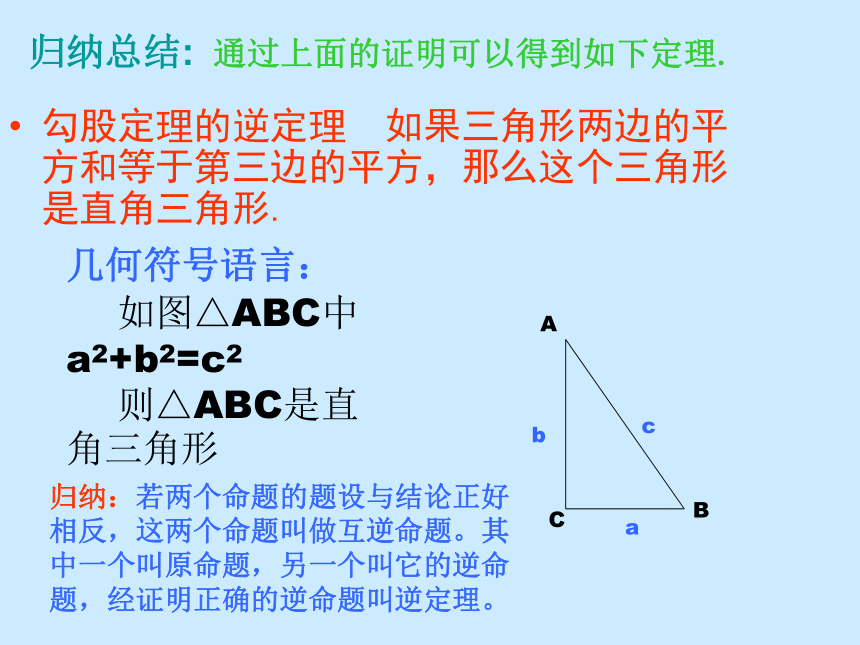
求证:∠C=90°.归纳总结: 通过上面的证明可以得到如下定理.勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.几何符号语言:
如图△ABC中 a2+b2=c2
则△ABC是直角三角形归纳:若两个命题的题设与结论正好相反,这两个命题叫做互逆命题。其中一个叫原命题,另一个叫它的逆命题,经证明正确的逆命题叫逆定理。例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形。如果是,指出哪条边所对的角是直角?
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
解(1)∵最大边是c=17,c2=289,
a2+b2=225+64=289,∴a2+b2=c2,
∴△ABC是直角三角形,最大边c所对的角是直角.
第(2)题由同学们仿照上面自己解答.小试牛刀 1、 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.
分析:在a、b、c三边中,哪一条边是最大的边?需要得出什么,才能证明△ABC为直角三角形?
请同学们自己完成证明过程.
能够成为直角三角形三条边长度的三个正整数,称为勾股数.
思考:除3、4、5外,再写出3组勾股数.想想看,可以怎样找?举一反三:1.判断下列三个边长组成的三角形是不是直角三角形?
(1)a=2,b=3,c=4.
(2)a=9,b=7,c=12.
(3)a=25,b=20,c=15.
2.在△ABC中,三边长a、b、c满足(a+c)(a-c)=b2,则△ABC是什么三角形?
3.给你一根带有刻度的皮尺,你如何用它来判断课桌面的角是直角?用这种办法能判断柱子是否与地面垂直吗?学会了吗?例3 某港口位于东西方向的海岸线上,“远航”号. “海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行16海里. “海天”号每小时 航行12海里.它们 离开港口一个半小时后相距30海里.如果知道“远航”沿 东北方向航行,能知道“海天”号沿哪个方向航行吗?pERQSRN分析:由题意画出图形。若求出两艘轮船的航向所成的角,即可知海天号的航向了。解:根据题意画出如图.
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302, 即 PQ2+PR2=QR2,
所以∠QPR=90°.
由远航号沿东北方向航行可知, ∠QPS=45°,
所以∠RPS=45°.即“海天”号沿西北方向航行.pERQSRN 通过本节课的学习,你有哪些收获?
1.勾股定理的逆定理.
2.勾股定理与它的逆定理之间有何关系?
3.勾股定理的逆定理是如何证明的?
4.应用该定理的基本步骤有哪些?成长的足迹
为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?猜想: 如果一个三角形的三边长a、b、c满足下面的关系a2+b2=c2,那么这个三角形是直角三角形吗? 证明 作△A’B’C’,使∠C’=90°,
A’C’=b,B’C’=a,如图(2),
那么A’B’2=a2+b2.(勾股定理)
又∵a2+b2=c2,(已知)
∴A’B’2=c2,A’B’=c (A’B’>0)
在ABC和A’B’C’中,
∵BC=a=B’C’,
CA=b=C’A’,
AB=c=A’B’,
∴△ABC≌△A’B’C’(SSS) ∴∠C=∠C’=90°,
∴△ABC是直角三角形.已知:在△ABC中,AB=c,BC=a,AC=b,并且a2+b2=c2,如图(1).
求证:∠C=90°.归纳总结: 通过上面的证明可以得到如下定理.勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.几何符号语言:
如图△ABC中 a2+b2=c2
则△ABC是直角三角形归纳:若两个命题的题设与结论正好相反,这两个命题叫做互逆命题。其中一个叫原命题,另一个叫它的逆命题,经证明正确的逆命题叫逆定理。例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形。如果是,指出哪条边所对的角是直角?
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
解(1)∵最大边是c=17,c2=289,
a2+b2=225+64=289,∴a2+b2=c2,
∴△ABC是直角三角形,最大边c所对的角是直角.
第(2)题由同学们仿照上面自己解答.小试牛刀 1、 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.
分析:在a、b、c三边中,哪一条边是最大的边?需要得出什么,才能证明△ABC为直角三角形?
请同学们自己完成证明过程.
能够成为直角三角形三条边长度的三个正整数,称为勾股数.
思考:除3、4、5外,再写出3组勾股数.想想看,可以怎样找?举一反三:1.判断下列三个边长组成的三角形是不是直角三角形?
(1)a=2,b=3,c=4.
(2)a=9,b=7,c=12.
(3)a=25,b=20,c=15.
2.在△ABC中,三边长a、b、c满足(a+c)(a-c)=b2,则△ABC是什么三角形?
3.给你一根带有刻度的皮尺,你如何用它来判断课桌面的角是直角?用这种办法能判断柱子是否与地面垂直吗?学会了吗?例3 某港口位于东西方向的海岸线上,“远航”号. “海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行16海里. “海天”号每小时 航行12海里.它们 离开港口一个半小时后相距30海里.如果知道“远航”沿 东北方向航行,能知道“海天”号沿哪个方向航行吗?pERQSRN分析:由题意画出图形。若求出两艘轮船的航向所成的角,即可知海天号的航向了。解:根据题意画出如图.
PQ=16×1.5=24,
PR=12×1.5=18,
QR=30.
因为242+182=302, 即 PQ2+PR2=QR2,
所以∠QPR=90°.
由远航号沿东北方向航行可知, ∠QPS=45°,
所以∠RPS=45°.即“海天”号沿西北方向航行.pERQSRN 通过本节课的学习,你有哪些收获?
1.勾股定理的逆定理.
2.勾股定理与它的逆定理之间有何关系?
3.勾股定理的逆定理是如何证明的?
4.应用该定理的基本步骤有哪些?成长的足迹
