2.4一元一次不等式第1课时 课件(共23张PPT)-2023-2024学年八年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.4一元一次不等式第1课时 课件(共23张PPT)-2023-2024学年八年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 06:25:21 | ||
图片预览








文档简介
北师大版 数学 八年级下册
第1课时
第二章 一元一次不等式与一元一次不等式组
4 一元一次不等式
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上;(重点)
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤.(难点)
复习回顾
1.能使不等式成立的未知数的值,叫做 .
2.一个含有未知数的不等式的 ,组成这个不等式的解集.
3. 的过程叫做解不等式.
4.数轴上表示要点:大于向 ,小于向 ;有等号用实心点,无等号用 .
不等式的解
所有解
求不等式解集
右
左
空心圈
一、创设情境,引入新知
解:移项,得 -x-2x=6-3;
合并同类项,得 -3x=3;
系数化为1,得 x=-1.
你还记得如何解一元一次方程吗?
解方程:3-x=2x+6
如何解不等式?????????????≥?????????????呢?下面我们一起来探讨!
?
二、自主合作,探究新知
探究一:一元一次不等式的概念
①不等式的两边都是整式;
②只含有一个未知数;
③未知数的最高次数是一次.
根据一元一次方程的概念,你们能归纳出一元一次不等式的概念吗?
观察下列不等式:
(1)6+3x>30;(2)x+17<5x;(3)x>5;(4)????????.????????×????????????>????????????.
这些不等式有哪些共同特点?
?
二、自主合作,探究新知
不等式的两边都是整式,只含有一个未知数,且未知数的最高次数是1的不等式,叫做一元一次不等式.
知识要点
想一想:在前面几节课中,你列出了哪些一元一次不等式?试举两例,并与同伴进行交流.
一元一次不等式的概念:
下列不等式是一元一次不等式吗?
(1)x-7y>26;
(2)3xy< 2x+1;
(3)-4x>3;
(4)????????????>50;
(5)????????>1.
?
二、自主合作,探究新知
×
√
×
√
×
跟踪练习
二、自主合作,探究新知
探究二:解一元一次不等式
这个不等式的解集在数轴上表示如下:
做一做:你能类比解一元一次方程,求解一元一次不等式吗?
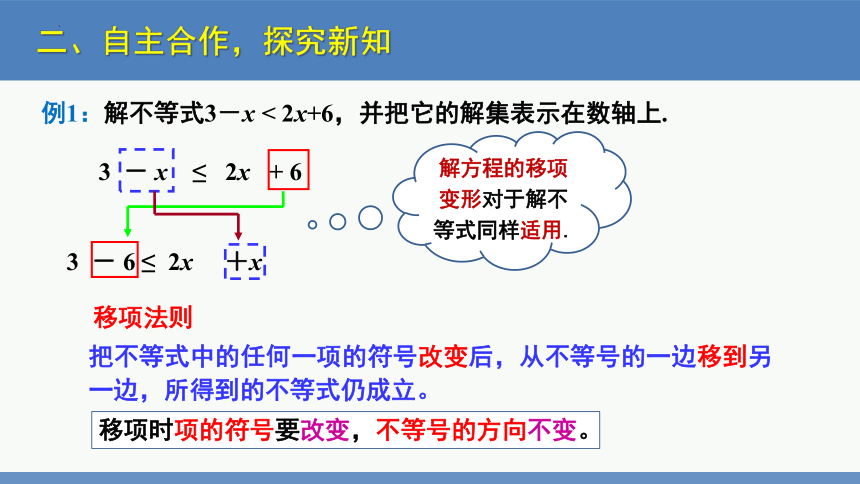
例1:解不等式3-x < 2x+6,并把它的解集表示在数轴上.
解:两边都加-2x,得 3-x-2x< 2x+6-2x;
合并同类项,得 3-3x < 6;
两边都加-3,得 -3x < 3;
两边都除以-3,得 x >-1.
二、自主合作,探究新知
3 - x ≤ 2x + 6
3 - 6 ≤ 2x +x
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立。
移项法则
移项时项的符号要改变,不等号的方向不变。
例1:解不等式3-x < 2x+6,并把它的解集表示在数轴上.
解方程的移项变形对于解不等式同样适用.
二、自主合作,探究新知
去括号,得 3x-6≥14-2x
移项、合并同类项,得 5x≥20
两边都除以5,得 x≥4
解:
去分母,得 3(x-2) ≥2(7-x)
这个不等式的解集在数轴上表示如下:
2
3
1
4
5
6
0
-1
-2
2
3
1
4
5
6
0
-1
-2
典型例题
例2:解不等式?????????????≥?????????????,并把它的解集表示在数轴上.
?
知识要点
二、自主合作,探究新知
解一元一次不等式的一般步骤:
(1)去分母——不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
(3)移项——移项法则(不等式性质1)注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
二、自主合作,探究新知
典型例题
解: 去分母,得 2( 1 ?2x)≥ 4 ?3x
去括号,得 2?4x ≥ 4 ?3x
移项,合并同类项,得 ?x ≥ 2
两边都除以?1,得 x ≤ ?2
这个不等式的解集在数轴上表示如下:
例3:解不等式?????????????????≥?????????????????,并把它 的解集表示在数轴上.
?
思考:解一元一次不等式的过程和解一元一次方程有什么区别与联系?
一元一次方程
一元一次不等式
解
法
步
骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
二、自主合作,探究新知
3.不等式2x-1≤3的解集在数轴上的表示正确的是( )
三、即学即练,应用知识
D
2.不等式-x+2≥0的解集为( )A.x≥-2 B.x≤-2 C.x≥2 D.x≤2
D
C
1.下列不等式中,是一元一次不等式的是 ( )A.x2+3>2x B.????????-3>0 C.x-3>2y D.3y>-3
?
6.不等式????????+?????????
5.已知不等式????????-1>x与ax-6>5x的解集相同,则a= .
?
4.请写出一个解集为x>1的一元一次不等式: .
三、即学即练,应用知识
x-1>0
-3
2
7.对于任意实数a,b,定义一种运算:a※b=ab-a+b-2.例如,2※5=2×5-2+5-2=11.请根据上述的定义解决问题:若不等式3※x<2,则不等式的正整数解是 .
1
三、即学即练,应用知识
8.解下列不等式: (1)6x≤2x-24; (2)3x-5<2(2+3x);
解: (1)移项,得 6x-2x≤-24.合并同类项,得 4x≤-24.两边都除以4,得 x≤-6.
解: (2)去括号,得 3x-5<4+6x.移项、合并同类项,得 -3x<9.两边都除以-3,得 x>-3.
三、即学即练,应用知识
(3)5(x-3)-2(x-4)>2; (4)??????????????????
解: (3)去括号,得 5x-15-2x+8>2.移项、合并同类项,得 3x>9.两边都除以3,得 x>3.
解: (4)去分母,得 5x-1<3(x+1).去括号、移项,得 5x-3x<3+1.合并同类项,得 2x<4.
两边都除以2,得 x<2.
四、课堂小结
一元一次不等式
概念
解一元一次不等式
注意:在①和⑤中,如果乘数或除数是负数,要把不等号的方向改变.
步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化1.
不等式的两边都是整式,只含有一个未知数,且未知数的最高次数是1的不等式,叫做一元一次不等式.
3.不等式????+????????>????????+????????-1的正整数解的个数是 ( )A.1 B.2 C.3 D.4
?
1.若(m+1)????????????-3>0是关于x的一元一次不等式,则m的值为( )A.±1 B.1 C.-1 D.0
?
2.如图,在数轴上所表示的是下列哪个一元一次不等式的解集( )
A.????????x>-1 B.????????(x+3)≥-3 C.x+1≥-1 D.-2x>4
?
五、当堂达标检测
B
C
D
6.若代数式????+????????+1的值不小于????+????????-1的值,则x的取值范围是 .
?
4.已知点P(2m-1,3)在第二象限,则m的取值范围是( )A.m>???????? B.m≥???????? C.m?
五、当堂达标检测
C
5.不等式x-1≥3x-7的正整数解有 个.
3
x≥-37
五、当堂达标检测
解: (1)去分母,得 4x+3≥3x.
移项,得4 x-3x≥-3.合并同类项,得 x≥-3.
这个不等式的解集在数轴上的表示如下:
解: (2)去分母,得 2(x-1)≥x-2+6.去括号、移项,得 2x-x≥-2+6+2.合并同类项,得 x≥6.这个不等式的解集在数轴上的表示如下:
7.解下列不等式,并把它们的解集分别表示在数轴上: (1) ????????x+????????≥????????x; (2)x-1≥?????????????+3;
?
五、当堂达标检测
解: (3)去分母,得 2x>6-(x-3).
去括号,得 2x>6-x+3.移项、合并同类项,得 3x>9.
两边都除以3,得 x>3.这个不等式的解集在数轴上的表示如下:
解: (4)去分母,得 2(x-2)-5(x+4)>-30.去括号,得 2x-4-5x-20>-30.移项、合并同类项,得 -3x>-6.两边都除以-3,得 x<2.这个不等式的解集在数轴上的表示如下:
(3)????????>1??????????????; (4)??????????????????+????????>-3.
?
教材习题2.4.
六、布置作业
第1课时
第二章 一元一次不等式与一元一次不等式组
4 一元一次不等式
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上;(重点)
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤.(难点)
复习回顾
1.能使不等式成立的未知数的值,叫做 .
2.一个含有未知数的不等式的 ,组成这个不等式的解集.
3. 的过程叫做解不等式.
4.数轴上表示要点:大于向 ,小于向 ;有等号用实心点,无等号用 .
不等式的解
所有解
求不等式解集
右
左
空心圈
一、创设情境,引入新知
解:移项,得 -x-2x=6-3;
合并同类项,得 -3x=3;
系数化为1,得 x=-1.
你还记得如何解一元一次方程吗?
解方程:3-x=2x+6
如何解不等式?????????????≥?????????????呢?下面我们一起来探讨!
?
二、自主合作,探究新知
探究一:一元一次不等式的概念
①不等式的两边都是整式;
②只含有一个未知数;
③未知数的最高次数是一次.
根据一元一次方程的概念,你们能归纳出一元一次不等式的概念吗?
观察下列不等式:
(1)6+3x>30;(2)x+17<5x;(3)x>5;(4)????????.????????×????????????>????????????.
这些不等式有哪些共同特点?
?
二、自主合作,探究新知
不等式的两边都是整式,只含有一个未知数,且未知数的最高次数是1的不等式,叫做一元一次不等式.
知识要点
想一想:在前面几节课中,你列出了哪些一元一次不等式?试举两例,并与同伴进行交流.
一元一次不等式的概念:
下列不等式是一元一次不等式吗?
(1)x-7y>26;
(2)3xy< 2x+1;
(3)-4x>3;
(4)????????????>50;
(5)????????>1.
?
二、自主合作,探究新知
×
√
×
√
×
跟踪练习
二、自主合作,探究新知
探究二:解一元一次不等式
这个不等式的解集在数轴上表示如下:
做一做:你能类比解一元一次方程,求解一元一次不等式吗?
例1:解不等式3-x < 2x+6,并把它的解集表示在数轴上.
解:两边都加-2x,得 3-x-2x< 2x+6-2x;
合并同类项,得 3-3x < 6;
两边都加-3,得 -3x < 3;
两边都除以-3,得 x >-1.
二、自主合作,探究新知
3 - x ≤ 2x + 6
3 - 6 ≤ 2x +x
把不等式中的任何一项的符号改变后,从不等号的一边移到另一边,所得到的不等式仍成立。
移项法则
移项时项的符号要改变,不等号的方向不变。
例1:解不等式3-x < 2x+6,并把它的解集表示在数轴上.
解方程的移项变形对于解不等式同样适用.
二、自主合作,探究新知
去括号,得 3x-6≥14-2x
移项、合并同类项,得 5x≥20
两边都除以5,得 x≥4
解:
去分母,得 3(x-2) ≥2(7-x)
这个不等式的解集在数轴上表示如下:
2
3
1
4
5
6
0
-1
-2
2
3
1
4
5
6
0
-1
-2
典型例题
例2:解不等式?????????????≥?????????????,并把它的解集表示在数轴上.
?
知识要点
二、自主合作,探究新知
解一元一次不等式的一般步骤:
(1)去分母——不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
(3)移项——移项法则(不等式性质1)注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
二、自主合作,探究新知
典型例题
解: 去分母,得 2( 1 ?2x)≥ 4 ?3x
去括号,得 2?4x ≥ 4 ?3x
移项,合并同类项,得 ?x ≥ 2
两边都除以?1,得 x ≤ ?2
这个不等式的解集在数轴上表示如下:
例3:解不等式?????????????????≥?????????????????,并把它 的解集表示在数轴上.
?
思考:解一元一次不等式的过程和解一元一次方程有什么区别与联系?
一元一次方程
一元一次不等式
解
法
步
骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
二、自主合作,探究新知
3.不等式2x-1≤3的解集在数轴上的表示正确的是( )
三、即学即练,应用知识
D
2.不等式-x+2≥0的解集为( )A.x≥-2 B.x≤-2 C.x≥2 D.x≤2
D
C
1.下列不等式中,是一元一次不等式的是 ( )A.x2+3>2x B.????????-3>0 C.x-3>2y D.3y>-3
?
6.不等式????????+????????
5.已知不等式????????-1>x与ax-6>5x的解集相同,则a= .
?
4.请写出一个解集为x>1的一元一次不等式: .
三、即学即练,应用知识
x-1>0
-3
2
7.对于任意实数a,b,定义一种运算:a※b=ab-a+b-2.例如,2※5=2×5-2+5-2=11.请根据上述的定义解决问题:若不等式3※x<2,则不等式的正整数解是 .
1
三、即学即练,应用知识
8.解下列不等式: (1)6x≤2x-24; (2)3x-5<2(2+3x);
解: (1)移项,得 6x-2x≤-24.合并同类项,得 4x≤-24.两边都除以4,得 x≤-6.
解: (2)去括号,得 3x-5<4+6x.移项、合并同类项,得 -3x<9.两边都除以-3,得 x>-3.
三、即学即练,应用知识
(3)5(x-3)-2(x-4)>2; (4)?????????????????
解: (3)去括号,得 5x-15-2x+8>2.移项、合并同类项,得 3x>9.两边都除以3,得 x>3.
解: (4)去分母,得 5x-1<3(x+1).去括号、移项,得 5x-3x<3+1.合并同类项,得 2x<4.
两边都除以2,得 x<2.
四、课堂小结
一元一次不等式
概念
解一元一次不等式
注意:在①和⑤中,如果乘数或除数是负数,要把不等号的方向改变.
步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化1.
不等式的两边都是整式,只含有一个未知数,且未知数的最高次数是1的不等式,叫做一元一次不等式.
3.不等式????+????????>????????+????????-1的正整数解的个数是 ( )A.1 B.2 C.3 D.4
?
1.若(m+1)????????????-3>0是关于x的一元一次不等式,则m的值为( )A.±1 B.1 C.-1 D.0
?
2.如图,在数轴上所表示的是下列哪个一元一次不等式的解集( )
A.????????x>-1 B.????????(x+3)≥-3 C.x+1≥-1 D.-2x>4
?
五、当堂达标检测
B
C
D
6.若代数式????+????????+1的值不小于????+????????-1的值,则x的取值范围是 .
?
4.已知点P(2m-1,3)在第二象限,则m的取值范围是( )A.m>???????? B.m≥???????? C.m?
五、当堂达标检测
C
5.不等式x-1≥3x-7的正整数解有 个.
3
x≥-37
五、当堂达标检测
解: (1)去分母,得 4x+3≥3x.
移项,得4 x-3x≥-3.合并同类项,得 x≥-3.
这个不等式的解集在数轴上的表示如下:
解: (2)去分母,得 2(x-1)≥x-2+6.去括号、移项,得 2x-x≥-2+6+2.合并同类项,得 x≥6.这个不等式的解集在数轴上的表示如下:
7.解下列不等式,并把它们的解集分别表示在数轴上: (1) ????????x+????????≥????????x; (2)x-1≥?????????????+3;
?
五、当堂达标检测
解: (3)去分母,得 2x>6-(x-3).
去括号,得 2x>6-x+3.移项、合并同类项,得 3x>9.
两边都除以3,得 x>3.这个不等式的解集在数轴上的表示如下:
解: (4)去分母,得 2(x-2)-5(x+4)>-30.去括号,得 2x-4-5x-20>-30.移项、合并同类项,得 -3x>-6.两边都除以-3,得 x<2.这个不等式的解集在数轴上的表示如下:
(3)????????>1??????????????; (4)??????????????????+????????>-3.
?
教材习题2.4.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
