8.1 中学生的视力情况调查(第1课时) 课件(共38张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 8.1 中学生的视力情况调查(第1课时) 课件(共38张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 06:39:36 | ||
图片预览











文档简介
(共38张PPT)
第8章 统计和概率的简单应用
8.1 中学生的视力情况调查(1)
第1课时 简单随机抽样
学习目标
1. 理解抽样的广泛性和代表性;
2.了解简单随机抽样的概念,能用简单随机抽样的方法(如抽签等)从总体中抽取样本.
问题情境
你知道如何得到这些数据吗
知识回顾
某地区有25所中学,其中九年级学生共6000名.为了了解该地区九年级学生的视力情况,请你运用所学的统计知识,将解决上述问题所要经历的几个主要步骤进行排序.排序:_____________(只写序号)
①抽样调查;
②设计调查问卷;
③用样本估计总体;
④整理数据;
⑤分析数据.
②①④⑤③
如何收集数据呢?
尝试与交流
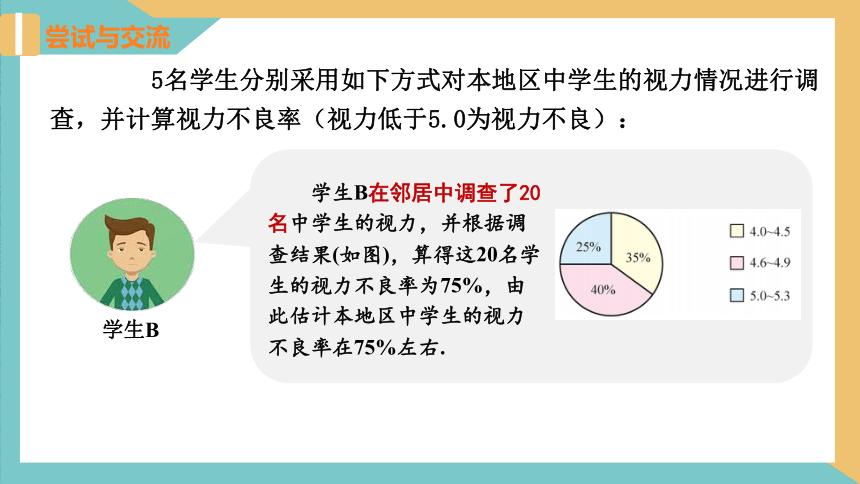
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生A
学生A在眼镜店调查了50名中学生的视力,并根据调查结果(如图),算得这50名学生的视力不良率为96%,由此估计本地区中学生的视力不良率超过95%.
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生B在邻居中调查了20名中学生的视力,并根据调查结果(如图),算得这20名学生的视力不良率为75%,由此估计本地区中学生的视力不良率在75%左右.
学生B
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生C调查了所在学校每个年级10名学生的视力,并根据调查结果(如图),算得这60名学生的视力不良率约为56.7%,由此估计本地区中学生的视力不良率接近60%.
学生C
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生D查阅了本地区每个中学医务室检查学生视力的资料,并计算出本地区中学生的视力不良率为66.1%.
学生D
学生E
学生E随机调查了本地区10%的中学生的视力,并通过对数据的整理、描述、分析,做出本地区中学生的视力不良率约为66.2%的估计.
讨论与交流
你对这5名学生的调查方式有何评价?请与同学交流.
学生A
在眼镜店调查了50名中学生的视力
学生B
在邻居中调查了20名中学生的视力
学生C
所在学校每个年级10名学生的视力
学生D
本地区每个中学医务室检查学生视力的资料
学生E
随机调查了本地区10%的中学生的视力
学生A、B、C都对本地区的特殊群体进行调查,所抽取的样本缺乏代表性,对总体的估计偏差较大.
学生E抽取的样本具有代表性,对总体的估计比较准确
学生D的调查为普查,工作量较大
归纳总结
在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性估计总体的相应特性,为了使估计、推断更加准确,抽样时要注意样本的代表性.
所谓代表性就是抽取的样本必须是随机的,即各个方面、各个层次的对象都要有所体现.
讨论与交流
要从某校九年级800名学生中抽查50名学生的视力,怎样抽取才能使样本具有代表性?
(3)从盒子中每次随机抽取一个号签(抽出的号签不放回),并记录其编号,连续抽取50次;
(1)将这800名学生依次编号(号码从1、2、…、800);
(2)将这800个号码写在形状、大小、质地都相同的号签上,放入一个盒子中搅匀;
(4)从总体中将与抽到的号签的编号相一致的个体取出,得到一个容量为50的样本.
方法如下:
编号
制签、
摇匀
抽签
取出
新知归纳
一般地,从个体总数为N的总体中抽取容量为n的样本(n新知归纳
抽签法、随机数表法、计算器(或计算机)产生随机数法.
简单随机抽样的方法:
注意:
(1)抽取的样本必须具有代表性;
(2)当总体个数不多时,宜采用抽签法,简单易行;
(3)当总体容量很大时,我们可以采用科学计算器 (或计算机)产生随机数法进行抽样.
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
(1)为了解某地区老年人的健康状况,在该地区医院里调查了100名老年病人1年内生病的次数;
例题讲解
解:(1)选取样本的方法不合适.因为这是对特殊群体进行调查,所抽取的样本必然带有特殊性,不具有代表性.
解:(2)选取样本的方法合适,在每100包方便面中,每个个体被抽到的可能性相同,符合简单随机抽样的抽样方法.
(2)某方便面厂家为了解产品质量情况,在其生产线上每100包随机抽取1包进行检查;
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
例题讲解
解:(3)选取样本的方法不合适.用某城市一个月的调查结果代替该市常年的空气污染情况,不符合简单随机抽样的抽样方法.
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
例题讲解
(3)为了解某城市的空气污染情况,调查了该城市某个月的空气污染情况.
例题讲解
例2 为检验某种产品的质量,质检员每天需要按时段抽检生产线上的该种产品30次,若以10min为一“段”,把0~24h分为144个时间段,试用简单随机抽样的方法确定这30个时间段(同一个时间段不能被重复抽取).
解:(1)将144个时间段依次编号为1~144;
(2)将编号写在形状、大小、质地都相同的纸条上,做成144个签,并
放在1个盒子中搅匀;
(3)每次从盒中抽出1个签(抽出的签不放回,每次抽签前要将盒中的签
搅匀),连续抽取30次,得到30个签,便确定出检验该种产品质量的30
个时间段.
1.当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是______;
A.对学校的同学发放问卷进行调查
B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查
D.对在路边行走的路人随机发放问卷进行调查
说出你的理由________________.
新知巩固
样本具有代表性
D
新知巩固
2.以下是一些来自媒体的信息,谈谈你读了之后有什么想法.
解: (1)不可信.因为这次调查的对象仅局限于对某高校校友的一次问卷调查,样本缺乏代表性.
(1)某报纸刊载:高校毕业生平均年收入为9万元;(数据来自对某高校校友的一次问卷调查)
新知巩固
(2)某医院自办的小报刊载:由于98%的人认为目前医药费用比较合理,因此目前医院各项收费总体而言是合理的 (数据来源于对该市所有医院的医务人员的一项问卷调查).
(2)“目前医院各项收费总体而言是合理的”这一结论不可信.因为调查选取的对象都是医务人员,对于整个社会群体尤其是就医者群体来说明显缺乏代表性.因此得出的相关结论很不可信.
新知巩固
3. 一个总体中有编号为1、2、3、4、5的5个个体,用简单随机抽样的方法从中抽取1个容量为2的样本,这样的样本共有多少个?写出所有可能的样本.
解:这样的样本共有10个,所有可能的样本为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).
新知巩固
4. 为了了解某校八年级学生每天完成家庭作业所用时长,该校数学兴趣小组对此展开抽样调查.已知八年级共25个班级,每班40名学生.
(1)小明选择对2班全体同学进行调查,小刚选择在学校门口随机抽取10名同学.他们的抽样是否合理?请分别说明理由.
解:(1)小明的抽样不合理.理由:全年级每个学生被抽到的机会不相等,样本不具有代表性;小刚的抽样不合理.理由:样本容量太小,样本不具有广泛性.
新知巩固
4. 为了了解某校八年级学生每天完成家庭作业所用时长,该校数学兴趣小组对此展开抽样调查.已知八年级共25个班级,每班40名学生.
(2)设样本容量为100,请设计一个合理的抽样调查方案.
解:(2)答案不唯一,如:数学兴趣小组从25个班级各随机抽取学号为9,19,29,39的4名同学进行调查.
5.在一次中学生知识竞赛中,主办方共拟定了20道文学题、15道历史题、15道地理题,并规定每名参赛选手要选答10道题,其中文学题4道、历史题3道、地理题3道,你认为应如何用简单随机抽样的方法确定这10道题?
解:将文学题编号为1,2,…,20,历史题编号为21,22,…,35,地理题编号为36,37,…,50,并将这些号码写在形状、大小、质地都相同的号签上,分装在3个不同的盒子中并搅匀.抽签时,先从装有编号为1,2,…,20的盒子中随机抽取4个号签,再分别从装有编号为21,22,…,35和36,37,…,50的盒子中各随机抽取3个号签,号签的号码所对应的题目就入选,从而确定出这名参赛选手要解答的10道题.
新知巩固
6.某班50名学生的身高如下(单位:cm):
150,148,159,156,157,163,156,164,156,159,169,163,170,162,163,164,155,162,153,155,177,165,160,161,166,159,161,157,155,167,162,165,159,147,163,172,156,165,157,164,152,156,153,164,165,162,167,151,175,162.
(1)计算这50名学生身高的平均数和方差;
解:(1)这50名学生身高的平均数是:(150+148+159++162)÷50=160.58(cm),
方差是:[(147-160.58)2+(148-160.58)2++(162-160.58)2)]÷50≈40.403 6(cm2);
新知巩固
(2)用简单随机抽样的方法,抽取样本容量为20的两个样本,并分别计算这两个样本的平均数和方差,所得的结果一致吗?与总体的平均数和方差一致吗?
(2) 根据题意得:
样本(1)是:177,165,160,161,166,159,161,157,155,167,162,165,159,147,163,172,156,165,157,164;
样本(2)是:162,165,159,147,163,172,156,165,157,164,152,156,153,164,165,162,167,151,175,162.
样本(1)的平均数是:(177+165 ++164)÷20=161.9(cm)
样本(1)的方差是:[(177-161.9)2+(165-161.9)2++(164-161.9)2)]≈39.09(cm2)
样本(2)的平均数是:(162+165 ++162)÷20=160.85(cm)
样本(2)的方差是:[(162-160.85)2+(165-160.85)2++(162-160.85)2)]≈46.8275(cm2)
(2)一般地,用简单随机抽样的方去抽取的两个样本的平均数和方差应大体上一致,它们与总体的平均数和方差也大体上一致.
新知巩固
课堂小结
8.1 中学生的视力情况调查(1)
简单随机抽样的概念
简单随机抽样的方法
当堂检测
1. 2020年为阻击新冠疫情,某社区要了解每一栋楼的居民年龄情况,以便有针对性进行防疫.一志愿者得到某栋楼60岁以上人的年龄(单位:岁)数据如下:62,63,75,79,68,85,82,69,70.获得这组数据的方法是( )
A.直接观察 B.实验 C.调查 D.测量
C
当堂检测
2. 某地区有8所高中和22所初中.要了解该地区中学生的视力情况,下列抽样方式获得的数据最能反映该地区中学生视力情况的是( )
A. 从该地区随机选取一所中学里的学生
B. 从该地区30所中学里随机选取800名学生
C. 从该地区一所高中和一所初中各选取一个年级的学生
D. 从该地区的22所初中里随机选取400名学生
B
当堂检测
3. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是__________.(填“全面调查”或“抽样调查”)
抽样调查
4. 某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:__________.
不合理
当堂检测
5. 某中学新建食堂正式投入使用,为提高服务质量,食堂管理人员对学生进行了“最受欢迎菜品”的调查统计,以下是打乱了的调查统计顺序,请按正确顺序重新排序 (只填序号)_____________.①绘制扇形图;
②收集最受学生欢迎菜品的数据;
③利用扇形图分析出受欢迎的统计图;
④整理所收集的数据.
②④①③
当堂检测
6. 有四位同学从编号为1~50的总体中抽取8个个体组成一个样本,他们选取的样本中个体编号如下:
①5,10,15,20,25,30,35,40;
②1,3,5,7,9,11,13,15;
③43,2,25,17,35,9,24,19;
④43,44,45,46,47,48,49,50.
你认为具有随机性的样本是____.(填序号)
③
7. 一个总体中有编号为a,b,c,d的4个个体,若用简单随机抽样的方法从中抽取1个容量为3的样本,则所有可能出现的样本为__________________________________________.
当堂检测
(a,b,c),(a,b,d),(a,c,d),(b,c,d)
当堂检测
8.判断下面的抽样调查选取样本的方法是否合理,并说明理由.
(1)在“五一”假期期间,调查某商场的日营业额,以估计该商场全年营业额;
解:不合理,因为“五一”是节假日,所以营业额会比平常高,样本不具有代表性.
(2)在大学生中调查我国青年上网目的的人数比例;
解:不合适,不具备代表性,因为青年包括的不仅仅是大学生,还有为数众多的非大学生,因此,大学生上网目的并不代表我国青年上网目的.
当堂检测
(3)放学时,在校门口随机调查50名学生关于学校环境卫生的意见,作为全校学生对学校环境卫生意见的一个样本;
解:合适,放学期间学生不分班级、性别、爱好等,基本上被随机“搅匀”,所以这样抽取的样本具有代表性,是合适的.
(4)为了检测一种新型计算机的性能指标,从中抽取2台进行测试.
解:不合理,因为只抽取2台,所以样本不具有代表性和广泛性.
当堂检测
9. 某校将学生体质健康测试成绩分为A、B、C、D四个等级,依次记为4分、3分、2分、1分.为了解学生整体体质健康状况,拟抽样进行统计分析.(1)以下是两位同学关于抽样方案的对话:
小红:“我想随机抽取七年级男、女生各60人的成绩.”小明:“我想随机抽取七、八、九年级男生各40人的成绩.”
根据图①中的学校信息,请你简要评价小红、小明的抽样方案.如果你来抽取120名学生的测试成绩,请给出抽样方案.
当堂检测
解:(1)两人都能根据学校信息合理选择样本容量进行抽样调查,小红的方案考虑到性别的差异,但没有考虑年级段的差异;小明的方案考虑到了年级段特点,但没有考虑到性别的差异,他们抽样调查不具有广泛性和代表性.
如果让我来抽取120名学生的测试成绩,应该随机抽取七、八、九年级男生、女生各20名的体质健康测试成绩.
当堂检测
(2)现将随机抽取的测试成绩整理并绘制成如图②所示统计图,请求出这组数据的平均数、中位数和众数.
解:(2)平均数为=2.75(分);抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列,处在中间位置的两个数都是3分,因此中位数是3分.
第8章 统计和概率的简单应用
8.1 中学生的视力情况调查(1)
第1课时 简单随机抽样
学习目标
1. 理解抽样的广泛性和代表性;
2.了解简单随机抽样的概念,能用简单随机抽样的方法(如抽签等)从总体中抽取样本.
问题情境
你知道如何得到这些数据吗
知识回顾
某地区有25所中学,其中九年级学生共6000名.为了了解该地区九年级学生的视力情况,请你运用所学的统计知识,将解决上述问题所要经历的几个主要步骤进行排序.排序:_____________(只写序号)
①抽样调查;
②设计调查问卷;
③用样本估计总体;
④整理数据;
⑤分析数据.
②①④⑤③
如何收集数据呢?
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生A
学生A在眼镜店调查了50名中学生的视力,并根据调查结果(如图),算得这50名学生的视力不良率为96%,由此估计本地区中学生的视力不良率超过95%.
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生B在邻居中调查了20名中学生的视力,并根据调查结果(如图),算得这20名学生的视力不良率为75%,由此估计本地区中学生的视力不良率在75%左右.
学生B
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生C调查了所在学校每个年级10名学生的视力,并根据调查结果(如图),算得这60名学生的视力不良率约为56.7%,由此估计本地区中学生的视力不良率接近60%.
学生C
尝试与交流
5名学生分别采用如下方式对本地区中学生的视力情况进行调查,并计算视力不良率(视力低于5.0为视力不良):
学生D查阅了本地区每个中学医务室检查学生视力的资料,并计算出本地区中学生的视力不良率为66.1%.
学生D
学生E
学生E随机调查了本地区10%的中学生的视力,并通过对数据的整理、描述、分析,做出本地区中学生的视力不良率约为66.2%的估计.
讨论与交流
你对这5名学生的调查方式有何评价?请与同学交流.
学生A
在眼镜店调查了50名中学生的视力
学生B
在邻居中调查了20名中学生的视力
学生C
所在学校每个年级10名学生的视力
学生D
本地区每个中学医务室检查学生视力的资料
学生E
随机调查了本地区10%的中学生的视力
学生A、B、C都对本地区的特殊群体进行调查,所抽取的样本缺乏代表性,对总体的估计偏差较大.
学生E抽取的样本具有代表性,对总体的估计比较准确
学生D的调查为普查,工作量较大
归纳总结
在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性估计总体的相应特性,为了使估计、推断更加准确,抽样时要注意样本的代表性.
所谓代表性就是抽取的样本必须是随机的,即各个方面、各个层次的对象都要有所体现.
讨论与交流
要从某校九年级800名学生中抽查50名学生的视力,怎样抽取才能使样本具有代表性?
(3)从盒子中每次随机抽取一个号签(抽出的号签不放回),并记录其编号,连续抽取50次;
(1)将这800名学生依次编号(号码从1、2、…、800);
(2)将这800个号码写在形状、大小、质地都相同的号签上,放入一个盒子中搅匀;
(4)从总体中将与抽到的号签的编号相一致的个体取出,得到一个容量为50的样本.
方法如下:
编号
制签、
摇匀
抽签
取出
新知归纳
一般地,从个体总数为N的总体中抽取容量为n的样本(n
抽签法、随机数表法、计算器(或计算机)产生随机数法.
简单随机抽样的方法:
注意:
(1)抽取的样本必须具有代表性;
(2)当总体个数不多时,宜采用抽签法,简单易行;
(3)当总体容量很大时,我们可以采用科学计算器 (或计算机)产生随机数法进行抽样.
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
(1)为了解某地区老年人的健康状况,在该地区医院里调查了100名老年病人1年内生病的次数;
例题讲解
解:(1)选取样本的方法不合适.因为这是对特殊群体进行调查,所抽取的样本必然带有特殊性,不具有代表性.
解:(2)选取样本的方法合适,在每100包方便面中,每个个体被抽到的可能性相同,符合简单随机抽样的抽样方法.
(2)某方便面厂家为了解产品质量情况,在其生产线上每100包随机抽取1包进行检查;
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
例题讲解
解:(3)选取样本的方法不合适.用某城市一个月的调查结果代替该市常年的空气污染情况,不符合简单随机抽样的抽样方法.
例1 判断下列抽样调查选取样本的方法是否合适,并说明理由:
例题讲解
(3)为了解某城市的空气污染情况,调查了该城市某个月的空气污染情况.
例题讲解
例2 为检验某种产品的质量,质检员每天需要按时段抽检生产线上的该种产品30次,若以10min为一“段”,把0~24h分为144个时间段,试用简单随机抽样的方法确定这30个时间段(同一个时间段不能被重复抽取).
解:(1)将144个时间段依次编号为1~144;
(2)将编号写在形状、大小、质地都相同的纸条上,做成144个签,并
放在1个盒子中搅匀;
(3)每次从盒中抽出1个签(抽出的签不放回,每次抽签前要将盒中的签
搅匀),连续抽取30次,得到30个签,便确定出检验该种产品质量的30
个时间段.
1.当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是______;
A.对学校的同学发放问卷进行调查
B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查
D.对在路边行走的路人随机发放问卷进行调查
说出你的理由________________.
新知巩固
样本具有代表性
D
新知巩固
2.以下是一些来自媒体的信息,谈谈你读了之后有什么想法.
解: (1)不可信.因为这次调查的对象仅局限于对某高校校友的一次问卷调查,样本缺乏代表性.
(1)某报纸刊载:高校毕业生平均年收入为9万元;(数据来自对某高校校友的一次问卷调查)
新知巩固
(2)某医院自办的小报刊载:由于98%的人认为目前医药费用比较合理,因此目前医院各项收费总体而言是合理的 (数据来源于对该市所有医院的医务人员的一项问卷调查).
(2)“目前医院各项收费总体而言是合理的”这一结论不可信.因为调查选取的对象都是医务人员,对于整个社会群体尤其是就医者群体来说明显缺乏代表性.因此得出的相关结论很不可信.
新知巩固
3. 一个总体中有编号为1、2、3、4、5的5个个体,用简单随机抽样的方法从中抽取1个容量为2的样本,这样的样本共有多少个?写出所有可能的样本.
解:这样的样本共有10个,所有可能的样本为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).
新知巩固
4. 为了了解某校八年级学生每天完成家庭作业所用时长,该校数学兴趣小组对此展开抽样调查.已知八年级共25个班级,每班40名学生.
(1)小明选择对2班全体同学进行调查,小刚选择在学校门口随机抽取10名同学.他们的抽样是否合理?请分别说明理由.
解:(1)小明的抽样不合理.理由:全年级每个学生被抽到的机会不相等,样本不具有代表性;小刚的抽样不合理.理由:样本容量太小,样本不具有广泛性.
新知巩固
4. 为了了解某校八年级学生每天完成家庭作业所用时长,该校数学兴趣小组对此展开抽样调查.已知八年级共25个班级,每班40名学生.
(2)设样本容量为100,请设计一个合理的抽样调查方案.
解:(2)答案不唯一,如:数学兴趣小组从25个班级各随机抽取学号为9,19,29,39的4名同学进行调查.
5.在一次中学生知识竞赛中,主办方共拟定了20道文学题、15道历史题、15道地理题,并规定每名参赛选手要选答10道题,其中文学题4道、历史题3道、地理题3道,你认为应如何用简单随机抽样的方法确定这10道题?
解:将文学题编号为1,2,…,20,历史题编号为21,22,…,35,地理题编号为36,37,…,50,并将这些号码写在形状、大小、质地都相同的号签上,分装在3个不同的盒子中并搅匀.抽签时,先从装有编号为1,2,…,20的盒子中随机抽取4个号签,再分别从装有编号为21,22,…,35和36,37,…,50的盒子中各随机抽取3个号签,号签的号码所对应的题目就入选,从而确定出这名参赛选手要解答的10道题.
新知巩固
6.某班50名学生的身高如下(单位:cm):
150,148,159,156,157,163,156,164,156,159,169,163,170,162,163,164,155,162,153,155,177,165,160,161,166,159,161,157,155,167,162,165,159,147,163,172,156,165,157,164,152,156,153,164,165,162,167,151,175,162.
(1)计算这50名学生身高的平均数和方差;
解:(1)这50名学生身高的平均数是:(150+148+159++162)÷50=160.58(cm),
方差是:[(147-160.58)2+(148-160.58)2++(162-160.58)2)]÷50≈40.403 6(cm2);
新知巩固
(2)用简单随机抽样的方法,抽取样本容量为20的两个样本,并分别计算这两个样本的平均数和方差,所得的结果一致吗?与总体的平均数和方差一致吗?
(2) 根据题意得:
样本(1)是:177,165,160,161,166,159,161,157,155,167,162,165,159,147,163,172,156,165,157,164;
样本(2)是:162,165,159,147,163,172,156,165,157,164,152,156,153,164,165,162,167,151,175,162.
样本(1)的平均数是:(177+165 ++164)÷20=161.9(cm)
样本(1)的方差是:[(177-161.9)2+(165-161.9)2++(164-161.9)2)]≈39.09(cm2)
样本(2)的平均数是:(162+165 ++162)÷20=160.85(cm)
样本(2)的方差是:[(162-160.85)2+(165-160.85)2++(162-160.85)2)]≈46.8275(cm2)
(2)一般地,用简单随机抽样的方去抽取的两个样本的平均数和方差应大体上一致,它们与总体的平均数和方差也大体上一致.
新知巩固
课堂小结
8.1 中学生的视力情况调查(1)
简单随机抽样的概念
简单随机抽样的方法
当堂检测
1. 2020年为阻击新冠疫情,某社区要了解每一栋楼的居民年龄情况,以便有针对性进行防疫.一志愿者得到某栋楼60岁以上人的年龄(单位:岁)数据如下:62,63,75,79,68,85,82,69,70.获得这组数据的方法是( )
A.直接观察 B.实验 C.调查 D.测量
C
当堂检测
2. 某地区有8所高中和22所初中.要了解该地区中学生的视力情况,下列抽样方式获得的数据最能反映该地区中学生视力情况的是( )
A. 从该地区随机选取一所中学里的学生
B. 从该地区30所中学里随机选取800名学生
C. 从该地区一所高中和一所初中各选取一个年级的学生
D. 从该地区的22所初中里随机选取400名学生
B
当堂检测
3. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是__________.(填“全面调查”或“抽样调查”)
抽样调查
4. 某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:__________.
不合理
当堂检测
5. 某中学新建食堂正式投入使用,为提高服务质量,食堂管理人员对学生进行了“最受欢迎菜品”的调查统计,以下是打乱了的调查统计顺序,请按正确顺序重新排序 (只填序号)_____________.①绘制扇形图;
②收集最受学生欢迎菜品的数据;
③利用扇形图分析出受欢迎的统计图;
④整理所收集的数据.
②④①③
当堂检测
6. 有四位同学从编号为1~50的总体中抽取8个个体组成一个样本,他们选取的样本中个体编号如下:
①5,10,15,20,25,30,35,40;
②1,3,5,7,9,11,13,15;
③43,2,25,17,35,9,24,19;
④43,44,45,46,47,48,49,50.
你认为具有随机性的样本是____.(填序号)
③
7. 一个总体中有编号为a,b,c,d的4个个体,若用简单随机抽样的方法从中抽取1个容量为3的样本,则所有可能出现的样本为__________________________________________.
当堂检测
(a,b,c),(a,b,d),(a,c,d),(b,c,d)
当堂检测
8.判断下面的抽样调查选取样本的方法是否合理,并说明理由.
(1)在“五一”假期期间,调查某商场的日营业额,以估计该商场全年营业额;
解:不合理,因为“五一”是节假日,所以营业额会比平常高,样本不具有代表性.
(2)在大学生中调查我国青年上网目的的人数比例;
解:不合适,不具备代表性,因为青年包括的不仅仅是大学生,还有为数众多的非大学生,因此,大学生上网目的并不代表我国青年上网目的.
当堂检测
(3)放学时,在校门口随机调查50名学生关于学校环境卫生的意见,作为全校学生对学校环境卫生意见的一个样本;
解:合适,放学期间学生不分班级、性别、爱好等,基本上被随机“搅匀”,所以这样抽取的样本具有代表性,是合适的.
(4)为了检测一种新型计算机的性能指标,从中抽取2台进行测试.
解:不合理,因为只抽取2台,所以样本不具有代表性和广泛性.
当堂检测
9. 某校将学生体质健康测试成绩分为A、B、C、D四个等级,依次记为4分、3分、2分、1分.为了解学生整体体质健康状况,拟抽样进行统计分析.(1)以下是两位同学关于抽样方案的对话:
小红:“我想随机抽取七年级男、女生各60人的成绩.”小明:“我想随机抽取七、八、九年级男生各40人的成绩.”
根据图①中的学校信息,请你简要评价小红、小明的抽样方案.如果你来抽取120名学生的测试成绩,请给出抽样方案.
当堂检测
解:(1)两人都能根据学校信息合理选择样本容量进行抽样调查,小红的方案考虑到性别的差异,但没有考虑年级段的差异;小明的方案考虑到了年级段特点,但没有考虑到性别的差异,他们抽样调查不具有广泛性和代表性.
如果让我来抽取120名学生的测试成绩,应该随机抽取七、八、九年级男生、女生各20名的体质健康测试成绩.
当堂检测
(2)现将随机抽取的测试成绩整理并绘制成如图②所示统计图,请求出这组数据的平均数、中位数和众数.
解:(2)平均数为=2.75(分);抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列,处在中间位置的两个数都是3分,因此中位数是3分.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
