8.1 中学生的视力情况调查(第2课时) 课件(共29张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 8.1 中学生的视力情况调查(第2课时) 课件(共29张PPT)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第8章 统计和概率的简单应用
8.1 中学生的视力情况调查(2)
第2课时 用简单随机抽样估算总体
学习目标
1. 能根据统计结果做出合理的判断和预测,体会统计对决策的作用;
2. 在收集、整理、描述和分析数据的活动中,发展统计观念.
问题情境
为了解某市七~九年级学生的视力情况,计划采用抽样调查的方法,从该市2万名七~九年级学生中抽查300名学生的视力,并进行整理分析.
问题1 本次调查的总体、样本各是什么?样本容量是多少?
问题2 如何抽取样本呢?
观察与思考
由于3个年级学生的视力有较明显的差异,所以我们采用简单随机抽样的方法从每个年级中各抽查100名学生的视力.整理如下:
视力 频数
七年级 八年级 九年级
4.0 0 0 0
4.1 0 0 1
4.2 0 0 2
4.3 0 0 1
4.4 0 3 6
4.5 0 6 5
4.6 4 5 6
七~九年级各100名学生的视力统计表
视力 频数
七年级 八年级 九年级
4.7 4 5 7
4.8 8 15 12
4.9 16 8 14
5.0 25 28 24
5.1 30 21 15
5.2 9 6 5
5.3 4 3 2
观察与思考
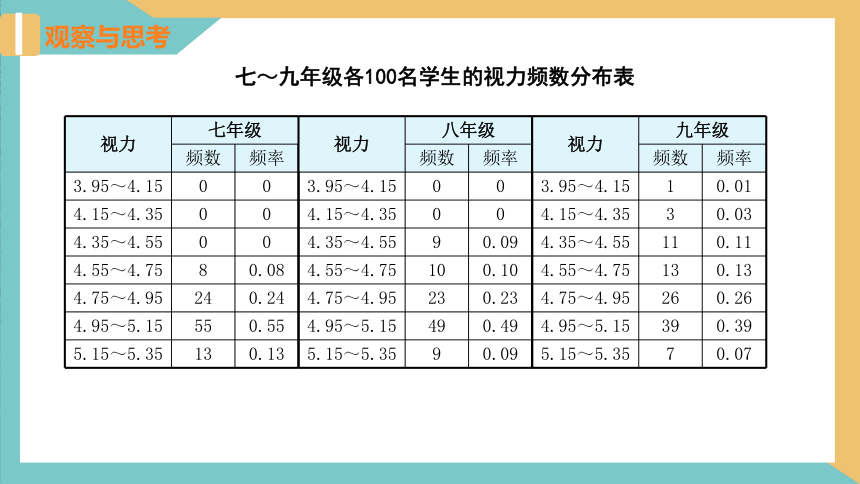
视力 七年级
频数 频率
3.95~4.15 0 0
4.15~4.35 0 0
4.35~4.55 0 0
4.55~4.75 8 0.08
4.75~4.95 24 0.24
4.95~5.15 55 0.55
5.15~5.35 13 0.13
七~九年级各100名学生的视力频数分布表
视力 八年级
频数 频率
3.95~4.15 0 0
4.15~4.35 0 0
4.35~4.55 9 0.09
4.55~4.75 10 0.10
4.75~4.95 23 0.23
4.95~5.15 49 0.49
5.15~5.35 9 0.09
视力 九年级
频数 频率
3.95~4.15 1 0.01
4.15~4.35 3 0.03
4.35~4.55 11 0.11
4.55~4.75 13 0.13
4.75~4.95 26 0.26
4.95~5.15 39 0.39
5.15~5.35 7 0.07
观察与思考
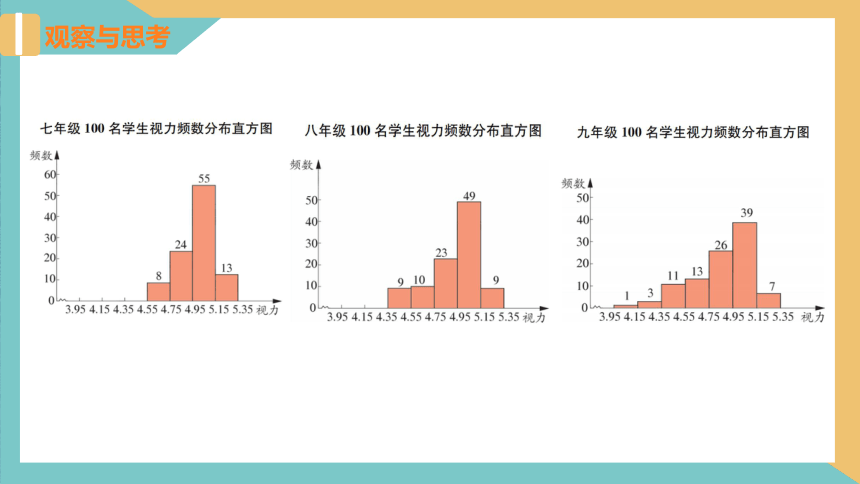
思考1 从上面的视力统计表、视力频数分布表和视力频数分布直方图中,你能获得哪些信息?
观察与思考
思考2 根据获得的信息,你对该市七~九年级学生的视力情况做怎样的分析、推断?
观察与思考
(1)七年级所抽查的学生的平均视力为5.0,中位数在4.95~5.15范围内,视力集中分布在4.75~5.15之间,约占学生总数的79%,视力不良率约为32%,该市七年级学生的视力变化范围相对较小.
(2)八年级所抽查的学生的平均视力为4.921,中位数在4.95~5.15范围内,视力集中分布在4.75~5.15之间,约占学生总数的72%,视力不良率约为42%,与七年级所抽查的学生的视力频数分布直方图相比,八年级所抽查的学生的视力频数分布直方图相对偏“左”,说明该市八年级学生的视力变化范围相对较大,低视力的比例相对增大.
观察与思考
(3)九年级所抽查的学生的平均视力为4.855,学生视力的中位数在4.75~4.95范围内,视力集中分布在4.75~5.15之间,约占学生总数的65%,视力不良率约为54%,与七年级所抽查的学生的视力频数分布直方图相比,九年级所抽查的学生的视力频数分布直方图明显偏“左”,说明该市九年级学生的视力变化范围明显变大,低视力的比例明显增大.
例题讲解
例 某校为了解九年级480名学生的数学学习情况,组织了一次检测,并采用简单随机抽样的方法从中抽取了部分学生的检测成绩进行分析,绘制成下表(72分及以上为“及格”,96分及以上为“优秀”,36分以下为“后进”):
(1)填写表中的空格;
50
0.02
2
0.06
4
0.18
14
0.20
0.02
80%
34%
2%
91
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(2)估计这480名学生本次检测成绩的中位数落在分数段83.5~95.5内.
50
0.02
2
0.06
4
0.18
14
0.20
0.02
80%
34%
2%
91
例题讲解
(3)将该校九年级学生本次数学检测的抽样成绩绘制成频数分布直方图,可以发现本次检测成绩总体上呈现“中间高,两头低”的分布,说明本次检测的可信度较好;估计该校九年级480名学生本次数学检测的平均成绩约为87.5分,及格率约为80%,优秀率约为 34%;估计该校九年级 480名学生本次检测的不及格率约为20%(其中后进率约为2%);估计该校九年级 480 名学生本次检测成绩高于95.5分的与低于83.5分的人数大体上各占一半.
(3)从两个不同角度对本次检测的总体情况做出评价.
例题讲解
新知巩固
1. 某市环保部门采用简单随机抽样的方法抽查了该市一年内30天的空气质量,结果如下:
其中,W≤50时,空气质量为优;50污染指数(W) 40 60 90 110 120
天数(t) 3 3 9 10 5
解: 365×=182.5(天)
该市一年中空气质量达到良以上的天数约为183天.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
根据提供的信息回答问题:
(1)该研究性学习小组抽取的样本容量是多少?
解:(1)3+6+9+8+4=30,
故该研究性学习小组抽取的样本容量是30.
(2)在所抽查的学生中,一天做家庭作业所用时间超过120 min的频率是多少?
解:(2)=0.4
故一天做家庭作业所用时间超过120 min的频率是0.4.
新知巩固
根据提供的信息回答问题:
(3)调查所得数据的中位数落在什么范围内?
解:(3)中位数是把这一组数据从小到大排列后,第15个数和第16个数的平均数,落在100.5~120.5min范围内.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
新知巩固
(4)你对该校九年级学生一天中做家庭作业所用时间做怎样的分析、推断?
解:(4)估计该校九年级能在100~120 min内完成一天的家庭作业的学生人数最多;估计有40%的学生一天中做家庭作业所用的时间超过120 min,只有10%的学生能在60~80 min内完成一天的家庭作业,可见该校学生的学习负担较重.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
根据提供的信息回答问题:
新知巩固
课堂小结
8.1 中学生的视力情况调查(2)
用简单随机抽样估算总体
掌握统计的全过程
当堂检测
1. 家务劳动是劳动教育的一个重要方面,教育部基础教育司发布通知要求家长引导孩子力所能及地做一些家务劳动.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别 一 二 三 四
劳动时间x/h
频数 10 20 12 8
根据表中的信息,下列说法正确的是 ( )
A.本次调查的样本容量是50人
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在四组
D.若七年级共有500名学生,估计平均每周在家劳动时间在四组的学生大约有100人
B
当堂检测
2. 某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么估计该工厂1200人中符合选拔条件的人数为________.
900
3. 小江为了估计某山区鸟群的数量,先捕捉40只鸟给它们分别做上标志,然后放回,等待有标志的鸟完全混合鸟群后,第二次捕捉120只鸟、发现其中4只有标志,则该山区的鸟群数量约有_____只.
1200
当堂检测
4.某校计划成立下列学生社团:
社团名称 文学社 话剧创作社 合唱团 生物实验小组 英语俱乐部
社团代号 A B C D E
为了解该校学生对上述社团的喜爱情况,学校从全体学生中随机抽取了部分学生进行问卷调查(每名学生必须选一个且只能选一个).根据统计数据,绘制了如下条形统计图和扇形统计图(部分信息未给出).
(1)该校此次共抽查了_____名学生;
50
(2)请补全条形统计图;
解:∵50-8-10-12-14=6(名),
∴选C的有6人,如图.
6
当堂检测
(3)若该校一共有1000名学生,请你根据调查统计的结果,试估计该校有多少名学生喜爱英语俱乐部.
解:∵1000×=280(名),
∴估计该校有280名学生喜爱英语俱乐部.
当堂检测
5. 为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、湿度)较快完成降解的环保塑料袋.调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查,使用情况为A(不使用),B(1~3个),C(4~6个),D(7个及以上),如图是根据调查结果绘制的统计图的一部分.
(1)本次调查的样本容量是________,请补全条形统计图;
解:(1)20÷20%=100,
所以本次调查的样本容量为100.
C类户数为100×25%=25,
B类户数为100-20-25-15=40.
100
25
40
当堂检测
(2) 已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理?请说明理由.
解:(2) 调查小组的估计合理.
理由:因为1500×=225(户),
所以该小区1周内使用7个及以上环保塑料袋的家庭约有225户.
当堂检测
6.为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.
(1)下面的抽取方法中,应该选择 ( )
A.从八年级随机抽取一个班的50名学生
B.从八年级女生中随机抽取50名学生
C.从八年级所有学生中随机抽取50名学生
C
当堂检测
阅读数量(本) 人数
0 5
1 25
2
3本及以上 5
合计 50
暑期课外阅读情况统计表
统计表中的______,补全条形统计图;
15
(2)对调查数据进行整理,得到下列两幅尚不完整的统计图表:
15
当堂检测
(3)若八年级共有800名学生,估计八年级学生暑期课外阅读数量达到2本及以上的学生人数;
解:(4) 本次调查大部分同学一周暑期课外阅读数量达不到3本,建议同学们多阅读,培养热爱读书的良好习惯(答案不唯一).
(4)根据上述调查情况,写一条你的看法.
解:(3) (人)
答:八年级学生暑期课外阅读数量达到2本及以上的学生约为320人.
当堂检测
7.李阿姨开了一家服装店,专门卖羽绒服,下面是2023年一年各月销售情况表.
月份 1 2 3 4 5 6 7 8 9 10 11 12
销量/件 100 90 50 11 8 6 4 6 5 30 80 110
根据表格提供的信息,回答下列问题:
(1)计算2023年各季度的销售情况,并用一个适当的统计图表示;
解:第一、二、三、四季度销售量分别为240件,25件,15件,220件.可用条形统计图表示,如答图①所示.
销量/件
季度
当堂检测
(2)计算2023年各季度销售量在全年销售总量中所占的百分比,并用适当的统计图表示;
解:全年销售总量为240+25+15+220=500(件).
第一、二、三、四季度销售量占销售总量的百分比分别为48%,5%,3%,44%.
可用扇形统计图表示,如答图②所示.
当堂检测
(3)从这些统计图表中,你能得出怎样的结论?请为李阿姨今后决策提供一些有用的建议.
解:从图表中可以看到第二、三季度的销售量少,第一、四季度的销售量多.建议旺季时多进羽绒服,淡季时转进其他商品或将店铺租给别人使用.
第8章 统计和概率的简单应用
8.1 中学生的视力情况调查(2)
第2课时 用简单随机抽样估算总体
学习目标
1. 能根据统计结果做出合理的判断和预测,体会统计对决策的作用;
2. 在收集、整理、描述和分析数据的活动中,发展统计观念.
问题情境
为了解某市七~九年级学生的视力情况,计划采用抽样调查的方法,从该市2万名七~九年级学生中抽查300名学生的视力,并进行整理分析.
问题1 本次调查的总体、样本各是什么?样本容量是多少?
问题2 如何抽取样本呢?
观察与思考
由于3个年级学生的视力有较明显的差异,所以我们采用简单随机抽样的方法从每个年级中各抽查100名学生的视力.整理如下:
视力 频数
七年级 八年级 九年级
4.0 0 0 0
4.1 0 0 1
4.2 0 0 2
4.3 0 0 1
4.4 0 3 6
4.5 0 6 5
4.6 4 5 6
七~九年级各100名学生的视力统计表
视力 频数
七年级 八年级 九年级
4.7 4 5 7
4.8 8 15 12
4.9 16 8 14
5.0 25 28 24
5.1 30 21 15
5.2 9 6 5
5.3 4 3 2
观察与思考
视力 七年级
频数 频率
3.95~4.15 0 0
4.15~4.35 0 0
4.35~4.55 0 0
4.55~4.75 8 0.08
4.75~4.95 24 0.24
4.95~5.15 55 0.55
5.15~5.35 13 0.13
七~九年级各100名学生的视力频数分布表
视力 八年级
频数 频率
3.95~4.15 0 0
4.15~4.35 0 0
4.35~4.55 9 0.09
4.55~4.75 10 0.10
4.75~4.95 23 0.23
4.95~5.15 49 0.49
5.15~5.35 9 0.09
视力 九年级
频数 频率
3.95~4.15 1 0.01
4.15~4.35 3 0.03
4.35~4.55 11 0.11
4.55~4.75 13 0.13
4.75~4.95 26 0.26
4.95~5.15 39 0.39
5.15~5.35 7 0.07
观察与思考
思考1 从上面的视力统计表、视力频数分布表和视力频数分布直方图中,你能获得哪些信息?
观察与思考
思考2 根据获得的信息,你对该市七~九年级学生的视力情况做怎样的分析、推断?
观察与思考
(1)七年级所抽查的学生的平均视力为5.0,中位数在4.95~5.15范围内,视力集中分布在4.75~5.15之间,约占学生总数的79%,视力不良率约为32%,该市七年级学生的视力变化范围相对较小.
(2)八年级所抽查的学生的平均视力为4.921,中位数在4.95~5.15范围内,视力集中分布在4.75~5.15之间,约占学生总数的72%,视力不良率约为42%,与七年级所抽查的学生的视力频数分布直方图相比,八年级所抽查的学生的视力频数分布直方图相对偏“左”,说明该市八年级学生的视力变化范围相对较大,低视力的比例相对增大.
观察与思考
(3)九年级所抽查的学生的平均视力为4.855,学生视力的中位数在4.75~4.95范围内,视力集中分布在4.75~5.15之间,约占学生总数的65%,视力不良率约为54%,与七年级所抽查的学生的视力频数分布直方图相比,九年级所抽查的学生的视力频数分布直方图明显偏“左”,说明该市九年级学生的视力变化范围明显变大,低视力的比例明显增大.
例题讲解
例 某校为了解九年级480名学生的数学学习情况,组织了一次检测,并采用简单随机抽样的方法从中抽取了部分学生的检测成绩进行分析,绘制成下表(72分及以上为“及格”,96分及以上为“优秀”,36分以下为“后进”):
(1)填写表中的空格;
50
0.02
2
0.06
4
0.18
14
0.20
0.02
80%
34%
2%
91
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(2)估计这480名学生本次检测成绩的中位数落在分数段83.5~95.5内.
50
0.02
2
0.06
4
0.18
14
0.20
0.02
80%
34%
2%
91
例题讲解
(3)将该校九年级学生本次数学检测的抽样成绩绘制成频数分布直方图,可以发现本次检测成绩总体上呈现“中间高,两头低”的分布,说明本次检测的可信度较好;估计该校九年级480名学生本次数学检测的平均成绩约为87.5分,及格率约为80%,优秀率约为 34%;估计该校九年级 480名学生本次检测的不及格率约为20%(其中后进率约为2%);估计该校九年级 480 名学生本次检测成绩高于95.5分的与低于83.5分的人数大体上各占一半.
(3)从两个不同角度对本次检测的总体情况做出评价.
例题讲解
新知巩固
1. 某市环保部门采用简单随机抽样的方法抽查了该市一年内30天的空气质量,结果如下:
其中,W≤50时,空气质量为优;50
天数(t) 3 3 9 10 5
解: 365×=182.5(天)
该市一年中空气质量达到良以上的天数约为183天.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
根据提供的信息回答问题:
(1)该研究性学习小组抽取的样本容量是多少?
解:(1)3+6+9+8+4=30,
故该研究性学习小组抽取的样本容量是30.
(2)在所抽查的学生中,一天做家庭作业所用时间超过120 min的频率是多少?
解:(2)=0.4
故一天做家庭作业所用时间超过120 min的频率是0.4.
新知巩固
根据提供的信息回答问题:
(3)调查所得数据的中位数落在什么范围内?
解:(3)中位数是把这一组数据从小到大排列后,第15个数和第16个数的平均数,落在100.5~120.5min范围内.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
新知巩固
(4)你对该校九年级学生一天中做家庭作业所用时间做怎样的分析、推断?
解:(4)估计该校九年级能在100~120 min内完成一天的家庭作业的学生人数最多;估计有40%的学生一天中做家庭作业所用的时间超过120 min,只有10%的学生能在60~80 min内完成一天的家庭作业,可见该校学生的学习负担较重.
2.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一天中做家庭作业所用时间(单位:min)进行了抽样调查,并把所得数据整理后绘制成频数分布直方图:
根据提供的信息回答问题:
新知巩固
课堂小结
8.1 中学生的视力情况调查(2)
用简单随机抽样估算总体
掌握统计的全过程
当堂检测
1. 家务劳动是劳动教育的一个重要方面,教育部基础教育司发布通知要求家长引导孩子力所能及地做一些家务劳动.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别 一 二 三 四
劳动时间x/h
频数 10 20 12 8
根据表中的信息,下列说法正确的是 ( )
A.本次调查的样本容量是50人
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在四组
D.若七年级共有500名学生,估计平均每周在家劳动时间在四组的学生大约有100人
B
当堂检测
2. 某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么估计该工厂1200人中符合选拔条件的人数为________.
900
3. 小江为了估计某山区鸟群的数量,先捕捉40只鸟给它们分别做上标志,然后放回,等待有标志的鸟完全混合鸟群后,第二次捕捉120只鸟、发现其中4只有标志,则该山区的鸟群数量约有_____只.
1200
当堂检测
4.某校计划成立下列学生社团:
社团名称 文学社 话剧创作社 合唱团 生物实验小组 英语俱乐部
社团代号 A B C D E
为了解该校学生对上述社团的喜爱情况,学校从全体学生中随机抽取了部分学生进行问卷调查(每名学生必须选一个且只能选一个).根据统计数据,绘制了如下条形统计图和扇形统计图(部分信息未给出).
(1)该校此次共抽查了_____名学生;
50
(2)请补全条形统计图;
解:∵50-8-10-12-14=6(名),
∴选C的有6人,如图.
6
当堂检测
(3)若该校一共有1000名学生,请你根据调查统计的结果,试估计该校有多少名学生喜爱英语俱乐部.
解:∵1000×=280(名),
∴估计该校有280名学生喜爱英语俱乐部.
当堂检测
5. 为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、湿度)较快完成降解的环保塑料袋.调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查,使用情况为A(不使用),B(1~3个),C(4~6个),D(7个及以上),如图是根据调查结果绘制的统计图的一部分.
(1)本次调查的样本容量是________,请补全条形统计图;
解:(1)20÷20%=100,
所以本次调查的样本容量为100.
C类户数为100×25%=25,
B类户数为100-20-25-15=40.
100
25
40
当堂检测
(2) 已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理?请说明理由.
解:(2) 调查小组的估计合理.
理由:因为1500×=225(户),
所以该小区1周内使用7个及以上环保塑料袋的家庭约有225户.
当堂检测
6.为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.
(1)下面的抽取方法中,应该选择 ( )
A.从八年级随机抽取一个班的50名学生
B.从八年级女生中随机抽取50名学生
C.从八年级所有学生中随机抽取50名学生
C
当堂检测
阅读数量(本) 人数
0 5
1 25
2
3本及以上 5
合计 50
暑期课外阅读情况统计表
统计表中的______,补全条形统计图;
15
(2)对调查数据进行整理,得到下列两幅尚不完整的统计图表:
15
当堂检测
(3)若八年级共有800名学生,估计八年级学生暑期课外阅读数量达到2本及以上的学生人数;
解:(4) 本次调查大部分同学一周暑期课外阅读数量达不到3本,建议同学们多阅读,培养热爱读书的良好习惯(答案不唯一).
(4)根据上述调查情况,写一条你的看法.
解:(3) (人)
答:八年级学生暑期课外阅读数量达到2本及以上的学生约为320人.
当堂检测
7.李阿姨开了一家服装店,专门卖羽绒服,下面是2023年一年各月销售情况表.
月份 1 2 3 4 5 6 7 8 9 10 11 12
销量/件 100 90 50 11 8 6 4 6 5 30 80 110
根据表格提供的信息,回答下列问题:
(1)计算2023年各季度的销售情况,并用一个适当的统计图表示;
解:第一、二、三、四季度销售量分别为240件,25件,15件,220件.可用条形统计图表示,如答图①所示.
销量/件
季度
当堂检测
(2)计算2023年各季度销售量在全年销售总量中所占的百分比,并用适当的统计图表示;
解:全年销售总量为240+25+15+220=500(件).
第一、二、三、四季度销售量占销售总量的百分比分别为48%,5%,3%,44%.
可用扇形统计图表示,如答图②所示.
当堂检测
(3)从这些统计图表中,你能得出怎样的结论?请为李阿姨今后决策提供一些有用的建议.
解:从图表中可以看到第二、三季度的销售量少,第一、四季度的销售量多.建议旺季时多进羽绒服,淡季时转进其他商品或将店铺租给别人使用.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
