9.4.1乘法公式-完全平方公式 课件(共27张PPT)-2023-2024学年七年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 9.4.1乘法公式-完全平方公式 课件(共27张PPT)-2023-2024学年七年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 42.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第9章整式乘法与因式分解
9.4.1乘法公式
-完全平方公式
教学目标
01
理解完全平方公式的几何背景和推导过程
02
能借助口诀牢记两个完全平方公式,并熟练运用于计算
03
熟悉完全平方公式的拓展公式
完全平方公式
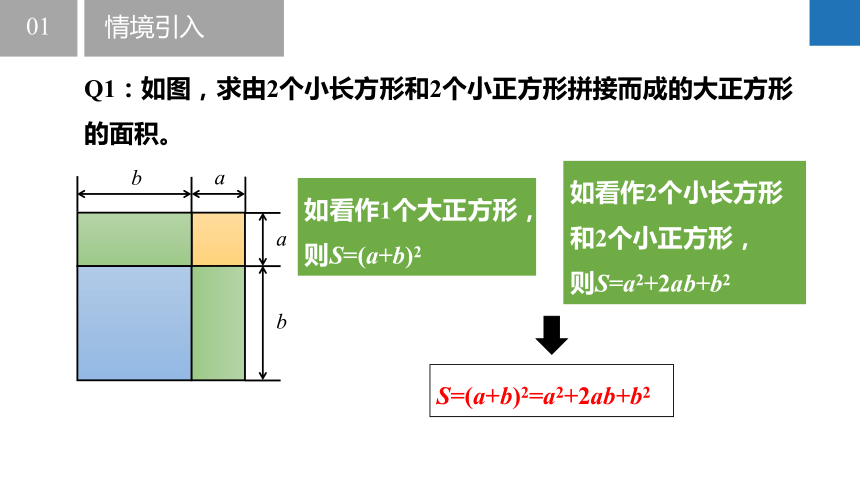
Q1:如图,求由2个小长方形和2个小正方形拼接而成的大正方形的面积。
如看作1个大正方形,
则S=(a+b)2
如看作2个小长方形和2个小正方形,
则S=a2+2ab+b2
a
b
a
b
01
情境引入
S=(a+b)2=a2+2ab+b2
请运用所学的知识验证(a+b)2=a2+2ab+b2的合理性~
【分析】
(a+b)2=(a+b)(a+b),
由多项式乘法的运算性质可得:
(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2。
01
情境引入
Q2:如图,大正方形由2个小长方形和2个小正方形拼接而成的,求蓝色小正方形的面积。
法一:S蓝=(a-b)2
法二:S蓝=a2-2ab+b2
01
情境引入
S蓝=(a-b)2=a2-2ab+b2
b
a
请运用所学的知识验证(a-b)2=a2-2ab+b2的合理性~
【分析】法一:
(a-b)2=(a-b)(a-b),
由多项式乘法的运算性质可得:
(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2。
01
情境引入
请运用所学的知识验证(a-b)2=a2-2ab+b2的合理性~
【分析】法二:
将a-b看作a+(-b),即将(-b)看作整体,则可直接套用公式:
(a+b)2=a2+2ab+b2
01
情境引入
[a+(-b)]2=a2+2·a·(-b)+(-b)2=a2-2ab+b2
-b
-b
-b
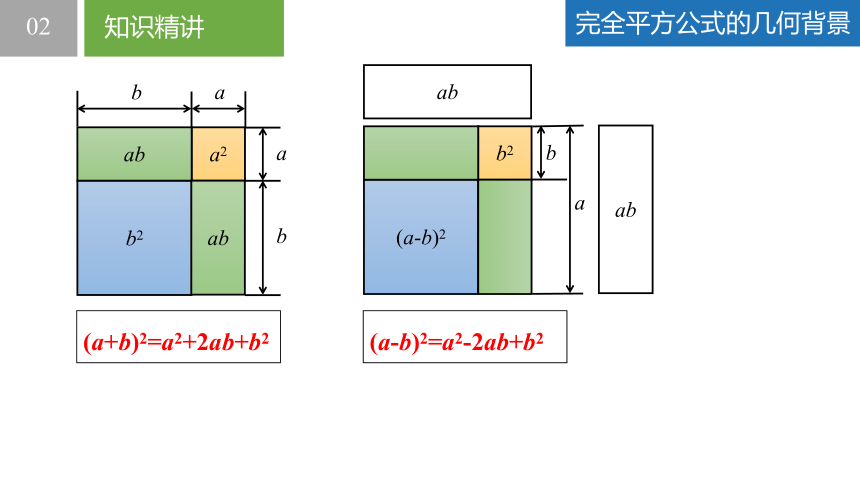
完全平方公式的几何背景
02
知识精讲
b2
a2
ab
a
b
a
b
ab
(a+b)2=a2+2ab+b2
(a-b)2
b2
b
a
ab
ab
(a-b)2=a2-2ab+b2
【完全平方公式】
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
【口诀】
首平方,末平方,
积的两倍在中央(符号随中央)。
完全平方公式
02
知识精讲
如何快速记忆这两个公式呢?
我们不妨从公式的结构特征进行分析。
平方
平方
积的2倍
符号跟随
【结构特征总结】
①左边是两个数的和(或差)的平方;
②右边是一个三项式,其中首末两项分别是两数的平方,都为正,中间一项是两数积的2倍,其符号与左边的运算符号相同。
完全平方公式
02
知识精讲
计算:(1)(2a+7b)2; (2)(xy-4)2。
【分析】
(1)原式=(2a)2+2·(2a)·(7b)+(7b)2
=4a2+28ab+49b2
将2a、7b分别看作整体,
则可直接套用公式:
(a+b)2=a2+2ab+b2
02
知识精讲
计算:(1)(2a+7b)2; (2)(xy-4)2。
【分析】
(2)原式=(xy)2-2·(xy)·4+42
=x2y2-8xy+16
将xy看作整体,
则可直接套用公式:
(a-b)2=a2-2ab+b2
02
知识精讲
【注意点】
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式。
完全平方公式
02
知识精讲
02
知识精讲
【乘法公式】
完全平方公式叫做乘法公式,在计算时可以直接使用。
乘法公式
例1、如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式( )
A.x2-y2=(x-y)(x+y) B.(x-y)2=x2-2xy+y2
C.(x+y)2=x2+2xy+y2 D.(x-y)2+4xy=(x+y)2
C
03
典例精析
例2、计算:(-3x-4y)2。
【分析】
∵互为相反数的两数的平方是相等的,
∴原式=(3x+4y)2,
03
典例精析
∴原式=(3x)2+2×(3x)·(4y)+(4y)2=9x2+24xy+16y2。
例3、已知(3x+a)2=9x2+bx+4,则b的值为( )
A.6 B.±6 C.12 D.±12
【分析】
∵(3x+a)2=9x2+6ax+a2=9x2+bx+4,
∴a2=4,b=6a,
∴a=±2,b=±12。
D
03
典例精析
例4、先化简,再求值:(a+b)2-(a-b)2+5a(a-b),其中a=3,b=2。
【分析】(a+b)2-(a-b)2+5a(a-b)
=a2+2ab+b2-(a2-2ab+b2)+5a2-5ab
=4ab+5a2-5ab
=5a2-ab,
03
典例精析
当a=3,b=2时,原式=5×9-3×2=39。
【总结】(a+b)2-(a-b)2=4ab
例5、计算:(1)10032; (2)99982。
【分析】
(1)10032
=(1000+3)2
=10002+2×1000×3+32
=1000000+6000+9
=1006009
(2)99982
=(10000-2)2
=100002-2×10000×2+22
=100000000-40000+4
=99960004
03
典例精析
完全平方公式的拓展
计算:(a+b+c)2。
大正方形的面积即(a+b+c)2
=3个小正方形与6个长方形的面积之和
=a2+b2+c2+2ab+2bc+2ca。
a
c
a
c
b
b
01
情境引入
【分析】法一:几何法
【分析】法二:多项式乘法的运算性质
01
情境引入
计算:(a+b+c)2。
原式=(a+b+c)(a+b+c)
=a2+ab+ac+ba+b2+bc+ca+cb+c2
=a2+b2+c2+2ab+2bc+2ca。
【分析】法三:完全平方公式
01
情境引入
计算:(a+b+c)2。
原式=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2bc+2ca。
将(a+b)看作整体,
则可直接套用公式:
(a+b)2=a2+2ab+b2
02
知识精讲
【拓展公式】
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
拓展公式
例、计算:(x-y-z)2。
【分析】
原式=[x+(-y)+(-z)]2
=x2+(-y)2+(-z)2+2x(-y)+2(-y)(-z)+2(-z)x
=x2+y2+z2-2xy+2yz-2zx
03
典例精析
将-y、-z分别看作整体,
则可直接套用公式:(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
课后总结
【完全平方公式】
(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2。
【口诀】首平方,末平方,积的两倍在中央(符号随中央)。
【结构特征总结】
①左边是两个数的和(或差)的平方;
②右边是一个三项式,其中首末两项分别是两数的平方,都为正,中间一项是两数积的2倍,其符号与左边的运算符号相同。
【注意点】
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式。
【拓展公式】
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
【乘法公式】
完全平方公式叫做乘法公式,在计算时可以直接使用。
第9章整式乘法与因式分解
9.4.1乘法公式
-完全平方公式
教学目标
01
理解完全平方公式的几何背景和推导过程
02
能借助口诀牢记两个完全平方公式,并熟练运用于计算
03
熟悉完全平方公式的拓展公式
完全平方公式
Q1:如图,求由2个小长方形和2个小正方形拼接而成的大正方形的面积。
如看作1个大正方形,
则S=(a+b)2
如看作2个小长方形和2个小正方形,
则S=a2+2ab+b2
a
b
a
b
01
情境引入
S=(a+b)2=a2+2ab+b2
请运用所学的知识验证(a+b)2=a2+2ab+b2的合理性~
【分析】
(a+b)2=(a+b)(a+b),
由多项式乘法的运算性质可得:
(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2。
01
情境引入
Q2:如图,大正方形由2个小长方形和2个小正方形拼接而成的,求蓝色小正方形的面积。
法一:S蓝=(a-b)2
法二:S蓝=a2-2ab+b2
01
情境引入
S蓝=(a-b)2=a2-2ab+b2
b
a
请运用所学的知识验证(a-b)2=a2-2ab+b2的合理性~
【分析】法一:
(a-b)2=(a-b)(a-b),
由多项式乘法的运算性质可得:
(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2。
01
情境引入
请运用所学的知识验证(a-b)2=a2-2ab+b2的合理性~
【分析】法二:
将a-b看作a+(-b),即将(-b)看作整体,则可直接套用公式:
(a+b)2=a2+2ab+b2
01
情境引入
[a+(-b)]2=a2+2·a·(-b)+(-b)2=a2-2ab+b2
-b
-b
-b
完全平方公式的几何背景
02
知识精讲
b2
a2
ab
a
b
a
b
ab
(a+b)2=a2+2ab+b2
(a-b)2
b2
b
a
ab
ab
(a-b)2=a2-2ab+b2
【完全平方公式】
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
【口诀】
首平方,末平方,
积的两倍在中央(符号随中央)。
完全平方公式
02
知识精讲
如何快速记忆这两个公式呢?
我们不妨从公式的结构特征进行分析。
平方
平方
积的2倍
符号跟随
【结构特征总结】
①左边是两个数的和(或差)的平方;
②右边是一个三项式,其中首末两项分别是两数的平方,都为正,中间一项是两数积的2倍,其符号与左边的运算符号相同。
完全平方公式
02
知识精讲
计算:(1)(2a+7b)2; (2)(xy-4)2。
【分析】
(1)原式=(2a)2+2·(2a)·(7b)+(7b)2
=4a2+28ab+49b2
将2a、7b分别看作整体,
则可直接套用公式:
(a+b)2=a2+2ab+b2
02
知识精讲
计算:(1)(2a+7b)2; (2)(xy-4)2。
【分析】
(2)原式=(xy)2-2·(xy)·4+42
=x2y2-8xy+16
将xy看作整体,
则可直接套用公式:
(a-b)2=a2-2ab+b2
02
知识精讲
【注意点】
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式。
完全平方公式
02
知识精讲
02
知识精讲
【乘法公式】
完全平方公式叫做乘法公式,在计算时可以直接使用。
乘法公式
例1、如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式( )
A.x2-y2=(x-y)(x+y) B.(x-y)2=x2-2xy+y2
C.(x+y)2=x2+2xy+y2 D.(x-y)2+4xy=(x+y)2
C
03
典例精析
例2、计算:(-3x-4y)2。
【分析】
∵互为相反数的两数的平方是相等的,
∴原式=(3x+4y)2,
03
典例精析
∴原式=(3x)2+2×(3x)·(4y)+(4y)2=9x2+24xy+16y2。
例3、已知(3x+a)2=9x2+bx+4,则b的值为( )
A.6 B.±6 C.12 D.±12
【分析】
∵(3x+a)2=9x2+6ax+a2=9x2+bx+4,
∴a2=4,b=6a,
∴a=±2,b=±12。
D
03
典例精析
例4、先化简,再求值:(a+b)2-(a-b)2+5a(a-b),其中a=3,b=2。
【分析】(a+b)2-(a-b)2+5a(a-b)
=a2+2ab+b2-(a2-2ab+b2)+5a2-5ab
=4ab+5a2-5ab
=5a2-ab,
03
典例精析
当a=3,b=2时,原式=5×9-3×2=39。
【总结】(a+b)2-(a-b)2=4ab
例5、计算:(1)10032; (2)99982。
【分析】
(1)10032
=(1000+3)2
=10002+2×1000×3+32
=1000000+6000+9
=1006009
(2)99982
=(10000-2)2
=100002-2×10000×2+22
=100000000-40000+4
=99960004
03
典例精析
完全平方公式的拓展
计算:(a+b+c)2。
大正方形的面积即(a+b+c)2
=3个小正方形与6个长方形的面积之和
=a2+b2+c2+2ab+2bc+2ca。
a
c
a
c
b
b
01
情境引入
【分析】法一:几何法
【分析】法二:多项式乘法的运算性质
01
情境引入
计算:(a+b+c)2。
原式=(a+b+c)(a+b+c)
=a2+ab+ac+ba+b2+bc+ca+cb+c2
=a2+b2+c2+2ab+2bc+2ca。
【分析】法三:完全平方公式
01
情境引入
计算:(a+b+c)2。
原式=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2bc+2ca。
将(a+b)看作整体,
则可直接套用公式:
(a+b)2=a2+2ab+b2
02
知识精讲
【拓展公式】
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
拓展公式
例、计算:(x-y-z)2。
【分析】
原式=[x+(-y)+(-z)]2
=x2+(-y)2+(-z)2+2x(-y)+2(-y)(-z)+2(-z)x
=x2+y2+z2-2xy+2yz-2zx
03
典例精析
将-y、-z分别看作整体,
则可直接套用公式:(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
课后总结
【完全平方公式】
(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2。
【口诀】首平方,末平方,积的两倍在中央(符号随中央)。
【结构特征总结】
①左边是两个数的和(或差)的平方;
②右边是一个三项式,其中首末两项分别是两数的平方,都为正,中间一项是两数积的2倍,其符号与左边的运算符号相同。
【注意点】
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和(或差)的平方的计算,都可以用这个公式。
【拓展公式】
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
【乘法公式】
完全平方公式叫做乘法公式,在计算时可以直接使用。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
