12.3 立方根和开立方 课件(共27张PPT)-2023-2024学年七年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 12.3 立方根和开立方 课件(共27张PPT)-2023-2024学年七年级数学下册同步精品课堂(沪教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 06:48:22 | ||
图片预览






文档简介
(共27张PPT)
12.3 立方根和开立方
2023-2024学年沪教版七年级下册数学课件
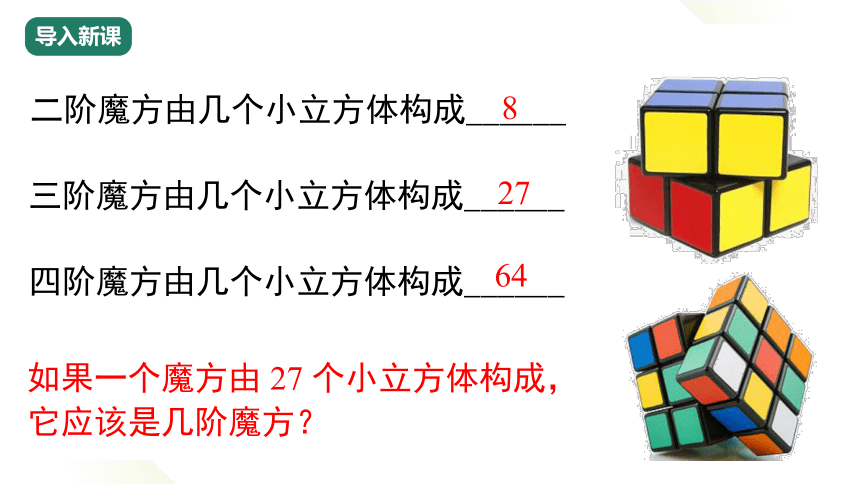
二阶魔方由几个小立方体构成______
三阶魔方由几个小立方体构成______
四阶魔方由几个小立方体构成______
如果一个魔方由 27 个小立方体构成,
它应该是几阶魔方?
8
27
64
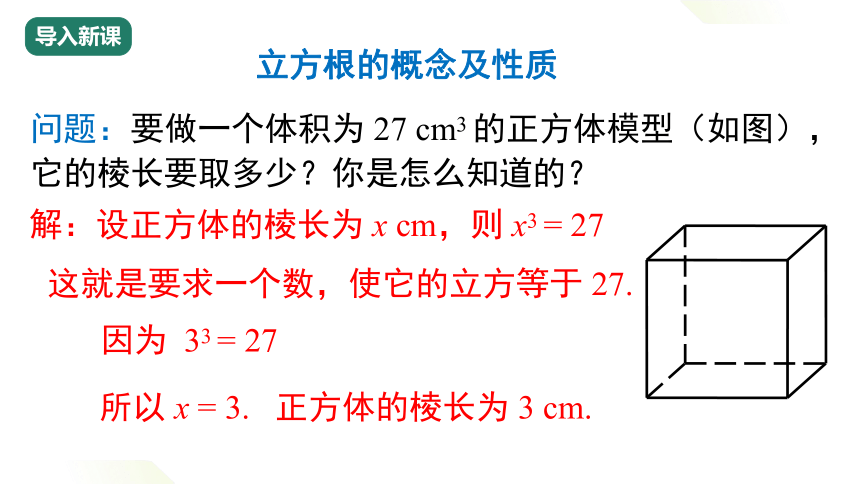
问题:要做一个体积为 27 cm3 的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
解:设正方体的棱长为 x cm,则 x3 = 27
这就是要求一个数,使它的立方等于 27.
因为 33 = 27
所以 x = 3. 正方体的棱长为 3 cm.
立方根的概念及性质
回忆:同学们能类比平方根的概念,平方根的性质,给出立方根的概念吗?
立方根的概念
一般地,一个数的立方等于 a,这个数就叫做 a 的立方根,也叫做 a 的三次方根.
如果 x3 = a,那么 x 叫做 a 的立方根.
根据立方根的意义填空:
因为 = 8,所以 8 的立方根是 ( );
因为( )3 = 0.125,所以 0.125 的立方根是 ( );
因为( )3 = 0,所以 0 的立方根是 ( );
因为( )3 = -8,所以 -8 的立方根是 ( );
因为( )3 = ,所以 的立方根是 ( ).
0
2
-2
0
-2
立方根的性质
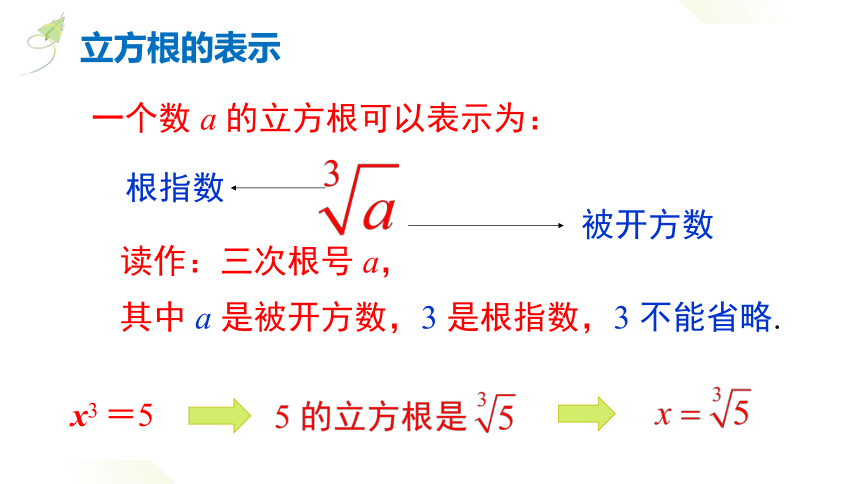
一个数 a 的立方根可以表示为:
根指数
被开方数
其中 a 是被开方数,3 是根指数,3 不能省略.
读作:三次根号 a,
立方根的表示
x3 =5
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
平方根与立方根的区别和联系
可以为任何数
非负数
例1 求下列各数的立方根:
(1) 1000;
(2)
教材第12页
(3) -0.001; (4) 0.
想一想
任意一个正数的立方根都是正数吗
正数的立方是一个正数,
负数的立方是一个负数,
零的立方等于零,
所以正数的立方根是一个正数,负数的立方根是一个负数,零的立方根是零.
互为逆运算
立方运算
开立方运算
如:( -2 )3=-8
-8 的立方根是 ( -2 )
立方根的性质
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
总结
立方根是它本身的数有 1,-1, 0;
平方根是它本身的数只有 0.
任意一个实数都有立方根,而且只有一个立方根.
在初中阶段,开立方运算中涉及的被开方数及立方根,都在实数范围内.
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ .
– 2
– 2
=
– 3
– 3
=
你能归纳出立方根的另一性质吗?
一般地,
=
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
例题2 求值:
教材第12页
一个数的立方根可能是有理数,也可能是无理数。我们可以利用计算器来求一个数的立方根或这个立方根的近似值.
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
问题 用计算器求下列各数的立方根:343, -1.331.
解:依次按键:
显示:7,所以
2ndF
4
3
3
=
依次按键:
显示:-1.1,所以
2ndF
1
(-)
.
3
1
3
=
用计算器求立方根
例3 用计算器求 的近似值(精确到 0.001).
解 : 依次按键:
显示:1.259 921 05
所以,
2ndF
=
2
例题4 用计算器,求值(近似值保留四位小数):
教材第13页
例题5 用计算器,求下列立方根,直接写出计算器显示的结果:
思考
比较例题4各小题中的被开方数和所得立方根,你有什么发现
教材第13页
用计算器计算 , , ,
,…,你能发现什么规律?用计算器计算
(精确到 0.001),并利用你发现的规律求
, , 的近似值.
被开方数的小数点向左或向右移动 3n 位时立方根的小数点就相应的向左或向右移动 n 位 (n 为正整数).
总结
= 0.06
= 0.6
= 6
= 60
探究
1.-8的立方根是 .
-2
2.若a的立方等于64,则a= .
4
3.面积为9的正方形,其边长等于( B )
A.9的平方根 B.9的算术平方根
C.9的立方根 D.的算术平方根
B
4.下列说法中正确的是( C )
A.0.09的平方根是0.3 B.=±4
C.0的立方根是0 D.1的立方根是±1
C
5.若m<0,则m的立方根是( A )
A. B.-
C.± D.
A
6.的立方根是 .
2
7.若x2=(-5)2,()3=-5,则x+y的值为______.
根据题意得x=-5或5,y=-5,
当x=-5,y=-5时,x+y=-5-5=-10;
当x=5,y=-5时,x+y=5-5=0.
解:
综上所述,x+y的值为-10或0.
12.计算:
(1)-3×++;
【解】-3×++
=-3×+(-10)+9
=-3×-10+9
=4-10+9=3.
(2)-+.
【解】-+
=-+
=--+
=-.
16.已知x+2是49的算术平方根,2x-y+10的立方根是2,求x2+y2的平方根.
【解】因为x+2是49的算术平方根,所以x+2=7,解得x=5.
因为2x-y+10的立方根是2,所以2x-y+10=8,解得y=12.
所以x2+y2=52+122=169.
因为(±13)2=169,
所以x2+y2的平方根是±13.
互为
逆运算
立方
立方根
定义
表示
特征
如果一个数的立方等于 a,那么这个数叫做 a 的________或三次方根.
正数 a 的平方根是_____;0 的平方根是_______;负数没有平方根
一个数 a 的立方根用符号表示为______,a 是________,3 是_______
开立方
立方根
被开方数
0
根指数
谢谢
12.3 立方根和开立方
2023-2024学年沪教版七年级下册数学课件
二阶魔方由几个小立方体构成______
三阶魔方由几个小立方体构成______
四阶魔方由几个小立方体构成______
如果一个魔方由 27 个小立方体构成,
它应该是几阶魔方?
8
27
64
问题:要做一个体积为 27 cm3 的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
解:设正方体的棱长为 x cm,则 x3 = 27
这就是要求一个数,使它的立方等于 27.
因为 33 = 27
所以 x = 3. 正方体的棱长为 3 cm.
立方根的概念及性质
回忆:同学们能类比平方根的概念,平方根的性质,给出立方根的概念吗?
立方根的概念
一般地,一个数的立方等于 a,这个数就叫做 a 的立方根,也叫做 a 的三次方根.
如果 x3 = a,那么 x 叫做 a 的立方根.
根据立方根的意义填空:
因为 = 8,所以 8 的立方根是 ( );
因为( )3 = 0.125,所以 0.125 的立方根是 ( );
因为( )3 = 0,所以 0 的立方根是 ( );
因为( )3 = -8,所以 -8 的立方根是 ( );
因为( )3 = ,所以 的立方根是 ( ).
0
2
-2
0
-2
立方根的性质
一个数 a 的立方根可以表示为:
根指数
被开方数
其中 a 是被开方数,3 是根指数,3 不能省略.
读作:三次根号 a,
立方根的表示
x3 =5
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
平方根与立方根的区别和联系
可以为任何数
非负数
例1 求下列各数的立方根:
(1) 1000;
(2)
教材第12页
(3) -0.001; (4) 0.
想一想
任意一个正数的立方根都是正数吗
正数的立方是一个正数,
负数的立方是一个负数,
零的立方等于零,
所以正数的立方根是一个正数,负数的立方根是一个负数,零的立方根是零.
互为逆运算
立方运算
开立方运算
如:( -2 )3=-8
-8 的立方根是 ( -2 )
立方根的性质
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
总结
立方根是它本身的数有 1,-1, 0;
平方根是它本身的数只有 0.
任意一个实数都有立方根,而且只有一个立方根.
在初中阶段,开立方运算中涉及的被开方数及立方根,都在实数范围内.
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ .
– 2
– 2
=
– 3
– 3
=
你能归纳出立方根的另一性质吗?
一般地,
=
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
例题2 求值:
教材第12页
一个数的立方根可能是有理数,也可能是无理数。我们可以利用计算器来求一个数的立方根或这个立方根的近似值.
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
问题 用计算器求下列各数的立方根:343, -1.331.
解:依次按键:
显示:7,所以
2ndF
4
3
3
=
依次按键:
显示:-1.1,所以
2ndF
1
(-)
.
3
1
3
=
用计算器求立方根
例3 用计算器求 的近似值(精确到 0.001).
解 : 依次按键:
显示:1.259 921 05
所以,
2ndF
=
2
例题4 用计算器,求值(近似值保留四位小数):
教材第13页
例题5 用计算器,求下列立方根,直接写出计算器显示的结果:
思考
比较例题4各小题中的被开方数和所得立方根,你有什么发现
教材第13页
用计算器计算 , , ,
,…,你能发现什么规律?用计算器计算
(精确到 0.001),并利用你发现的规律求
, , 的近似值.
被开方数的小数点向左或向右移动 3n 位时立方根的小数点就相应的向左或向右移动 n 位 (n 为正整数).
总结
= 0.06
= 0.6
= 6
= 60
探究
1.-8的立方根是 .
-2
2.若a的立方等于64,则a= .
4
3.面积为9的正方形,其边长等于( B )
A.9的平方根 B.9的算术平方根
C.9的立方根 D.的算术平方根
B
4.下列说法中正确的是( C )
A.0.09的平方根是0.3 B.=±4
C.0的立方根是0 D.1的立方根是±1
C
5.若m<0,则m的立方根是( A )
A. B.-
C.± D.
A
6.的立方根是 .
2
7.若x2=(-5)2,()3=-5,则x+y的值为______.
根据题意得x=-5或5,y=-5,
当x=-5,y=-5时,x+y=-5-5=-10;
当x=5,y=-5时,x+y=5-5=0.
解:
综上所述,x+y的值为-10或0.
12.计算:
(1)-3×++;
【解】-3×++
=-3×+(-10)+9
=-3×-10+9
=4-10+9=3.
(2)-+.
【解】-+
=-+
=--+
=-.
16.已知x+2是49的算术平方根,2x-y+10的立方根是2,求x2+y2的平方根.
【解】因为x+2是49的算术平方根,所以x+2=7,解得x=5.
因为2x-y+10的立方根是2,所以2x-y+10=8,解得y=12.
所以x2+y2=52+122=169.
因为(±13)2=169,
所以x2+y2的平方根是±13.
互为
逆运算
立方
立方根
定义
表示
特征
如果一个数的立方等于 a,那么这个数叫做 a 的________或三次方根.
正数 a 的平方根是_____;0 的平方根是_______;负数没有平方根
一个数 a 的立方根用符号表示为______,a 是________,3 是_______
开立方
立方根
被开方数
0
根指数
谢谢
