17.2.2勾股定理的逆定理的应用 课件(共24张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 17.2.2勾股定理的逆定理的应用 课件(共24张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
第17章
勾股定理
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
17.2.2
勾股定理的
逆定理的应用
条件
结论
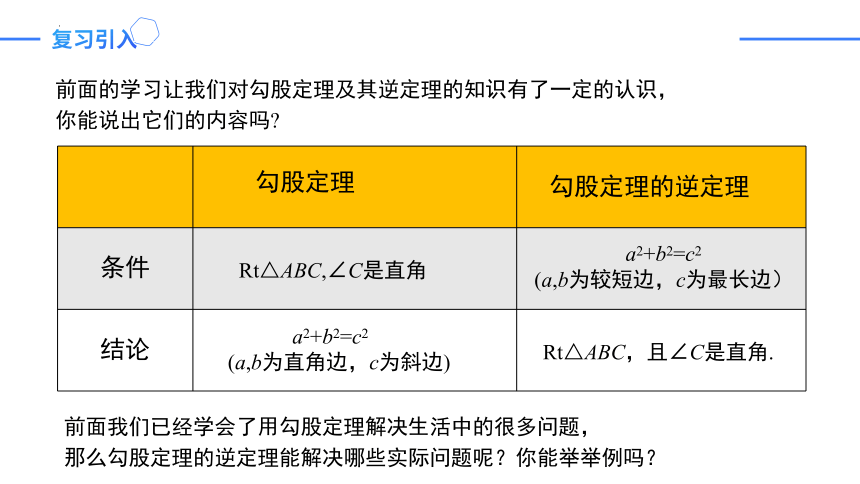
复习引入
前面的学习让我们对勾股定理及其逆定理的知识有了一定的认识,
你能说出它们的内容吗
a2+b2=c2
(a,b为直角边,c为斜边)
Rt△ABC,∠C是直角
勾股定理
勾股定理的逆定理
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
前面我们已经学会了用勾股定理解决生活中的很多问题,
那么勾股定理的逆定理能解决哪些实际问题呢?你能举举例吗?
典例精析
例1
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
(1)求四边形 ABCD 的面积.
A
B
C
D
∴ .
∴CD2+AC2=102+102=200,AD2= =200,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∵CD=10,AD=10 ,
解:连接 AC,
∵∠ABC=90°,AB=6,BC=8,
∴四边形ABCD的面积是
=74,
典例精析
例1
(2)求对角线 BD 的长.
解:作 DE⊥BC 交 BC 的延长线于点 E,则∠DEC=90°,
∵△ACD 是直角三角形,∠ACD=90°,
∴∠DCE+∠ACB=90°.
∵∠ABC=90°,
∴∠CAB+∠ACB=90°,
∴∠DCE=∠CAB.
A
B
C
D
E
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
典例精析
例1
(2)求对角线 BD 的长.
A
B
C
D
E
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
∴AB=CE,BC=ED.
∴ .
在△ABC 和△CED 中,
∴△ABC≌△CED(AAS).
∵AB=6,BC=8,
∴CE=6,ED=8,
∴BE=BC+CE=8+6=14,
典例精析
实际问题
抽象
数学模型
勾股定理及其逆定理
解答
实际意义
典例精析
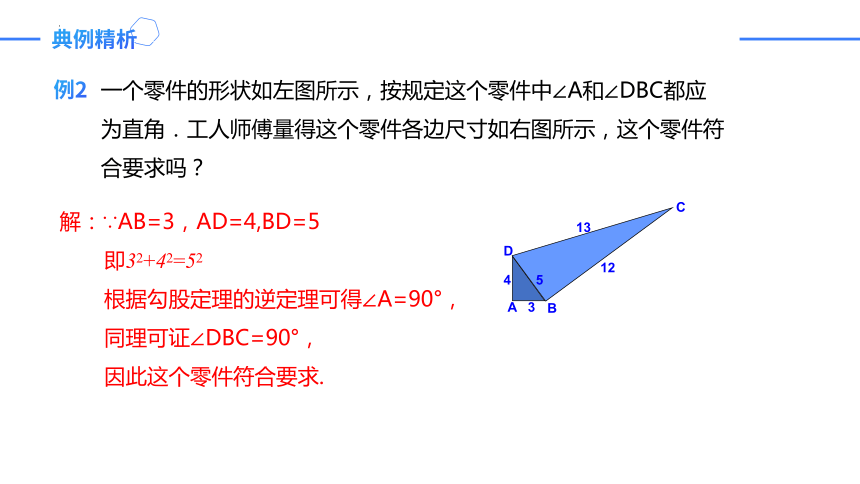
例2
13
A
B
C
D
3
4
5
12
一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
解:∵AB=3,AD=4,BD=5
即32+42=52
根据勾股定理的逆定理可得∠A=90°,
同理可证∠DBC=90°,
因此这个零件符合要求.
典例精析
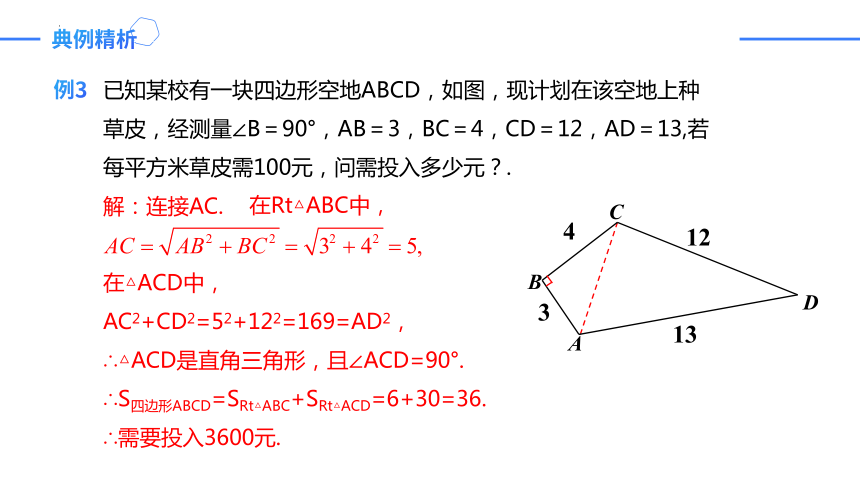
例3
已知某校有一块四边形空地ABCD,如图,现计划在该空地上种草皮,经测量∠B=90°,AB=3,BC=4,CD=12,AD=13,若每平方米草皮需100元,问需投入多少元?.
解:连接AC.
A
D
B
C
3
4
13
12
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
∴需要投入3600元.
典例精析
例4
典例精析
例4
典例精析
例5
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
1
2
N
E
P
Q
R
认真审题,弄清已知是什么?要解决的问题是什么?
由于我们现在所能得到的都是线段长,
要求角,由此你联想到了什么?
实质是要求出两艘船航向所成角.
勾股定理逆定理
问题1
问题2
勾股定理逆定理
典例精析
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
典例精析
例6
大型工程车行驶过程中会对周围产生较大的噪声影响.如图,有一台大型工程车沿公路 AB 由点 A 向点 B 行驶,已知点 C 为一所学校,且点 C 与直线
AB 上两点 A,B 的距离分别为 150 m 和 200 m,AB=250 m,大型工程车周围 130 m 以内为受噪声影响区域.
(1)学校 C 会受噪声影响吗?为什么?
B
A
C
(2)若大型工程车的行驶速度为 50 m/min,
大型工程车噪声影响该学校持续的时间
有多少分钟?
典例精析
例6
解:学校 C 会受噪声影响.
理由:如图,过点 C 作 CD⊥AB 于 D,
∵AC=150 m,BC=200 m,AB=250 m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∴S△ABC= AC·BC= CD·AB,
∴150×200=250CD,
∴CD= =120(m),
∵大型工程车周围 130 m 以内为受噪声影响区域,
∴学校 C 会受噪声影响.
A
B
C
D
典例精析
例6
∴EF=100(m).
(2)如图,取 EC=130 m,FC=130 m,当大型工程车在 EF 上时学校会受
噪声影响.
∵ED2=EC2-CD2=1302-1202=502,
∴ED=50(m),
∵大型工程车的行驶速度为 50 m/min,
∴100÷50=2(min),
即大型工程车噪声影响该学校持续的时间有 2 min.
E
F
A
B
C
D
典例精析
例7
锐角
钝角
>
<
典例精析
例7
归纳总结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
当堂检测
1.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
D
当堂检测
2.如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,AD= .
若AC⊥BC,求证:AD∥BC.
∴AD∥BC
当堂检测
3.如图,某中学为迎接校庆50周年,拟对学校校园中的一块空地进行美化
施工,已知AB=3 m,BC=4 m,∠ABC=90°,AD=12 m,CD=13 m,
学校欲在此空地上铺草坪,已知每平方米草坪80元,试问用草坪铺满这
块空地共需花费多少元.
解:如图,连接AC,在Rt△ABC中,
∵AC2=AB2+BC2=32+42=25,
∴AC=5 m.
∵AC2+AD2=52+122=169,CD2=132=169,
∴AC2+AD2=CD2,∴∠CAD=90°,
该区域面积=S△ACD-S△ABC=30-6=24(m2),
铺满这块空地共需花费24×80=1 920(元).
答:用草坪铺满这块空地共需花费1 920元.
当堂检测
A
B
C
D
M
N
北
东
4.一艘轮船从 A 港向南偏西 48°方向航行 100 km 到达 B 岛,再从 B 岛沿 BM 方向航行 125 km 到达 C 岛,A 港到航线 BM 的最短距离是 60 km.
(1)若轮船速度为 25 km/h,求轮船从 C 岛沿 CA 方向返回 A 港所需的时间;
∴ (km).
解:(1)由题意 AD=60 km,
在 Rt△ABD 中,由 AD2+BD2=AB2 得 602+BD2=1002.
∴BD=80(km).
∴CD=BC-BD=125-80=45(km).
75÷25=3(h).
答:从 C 岛沿 CA 方向返回 A 港所需的时间为 3 h.
当堂检测
(2)C 岛在 A 港的什么方向?
解:(2)∵AB2+AC2=1002+752=15 625,
BC2=1252=15 625,
∴AB2+AC2=BC2,
∴∠BAC=90°.
∴∠NAC=180°-90°-48°=42°.
∴C 岛在 A 港的北偏西 42°方向上.
A
B
C
D
M
N
北
东
第17章
勾股定理
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
17.2.2
勾股定理的
逆定理的应用
条件
结论
复习引入
前面的学习让我们对勾股定理及其逆定理的知识有了一定的认识,
你能说出它们的内容吗
a2+b2=c2
(a,b为直角边,c为斜边)
Rt△ABC,∠C是直角
勾股定理
勾股定理的逆定理
a2+b2=c2
(a,b为较短边,c为最长边)
Rt△ABC,且∠C是直角.
前面我们已经学会了用勾股定理解决生活中的很多问题,
那么勾股定理的逆定理能解决哪些实际问题呢?你能举举例吗?
典例精析
例1
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
(1)求四边形 ABCD 的面积.
A
B
C
D
∴ .
∴CD2+AC2=102+102=200,AD2= =200,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∵CD=10,AD=10 ,
解:连接 AC,
∵∠ABC=90°,AB=6,BC=8,
∴四边形ABCD的面积是
=74,
典例精析
例1
(2)求对角线 BD 的长.
解:作 DE⊥BC 交 BC 的延长线于点 E,则∠DEC=90°,
∵△ACD 是直角三角形,∠ACD=90°,
∴∠DCE+∠ACB=90°.
∵∠ABC=90°,
∴∠CAB+∠ACB=90°,
∴∠DCE=∠CAB.
A
B
C
D
E
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
典例精析
例1
(2)求对角线 BD 的长.
A
B
C
D
E
如图,在四边形ABCD中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10 .
∴AB=CE,BC=ED.
∴ .
在△ABC 和△CED 中,
∴△ABC≌△CED(AAS).
∵AB=6,BC=8,
∴CE=6,ED=8,
∴BE=BC+CE=8+6=14,
典例精析
实际问题
抽象
数学模型
勾股定理及其逆定理
解答
实际意义
典例精析
例2
13
A
B
C
D
3
4
5
12
一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
解:∵AB=3,AD=4,BD=5
即32+42=52
根据勾股定理的逆定理可得∠A=90°,
同理可证∠DBC=90°,
因此这个零件符合要求.
典例精析
例3
已知某校有一块四边形空地ABCD,如图,现计划在该空地上种草皮,经测量∠B=90°,AB=3,BC=4,CD=12,AD=13,若每平方米草皮需100元,问需投入多少元?.
解:连接AC.
A
D
B
C
3
4
13
12
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
∴需要投入3600元.
典例精析
例4
典例精析
例4
典例精析
例5
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
1
2
N
E
P
Q
R
认真审题,弄清已知是什么?要解决的问题是什么?
由于我们现在所能得到的都是线段长,
要求角,由此你联想到了什么?
实质是要求出两艘船航向所成角.
勾股定理逆定理
问题1
问题2
勾股定理逆定理
典例精析
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
典例精析
例6
大型工程车行驶过程中会对周围产生较大的噪声影响.如图,有一台大型工程车沿公路 AB 由点 A 向点 B 行驶,已知点 C 为一所学校,且点 C 与直线
AB 上两点 A,B 的距离分别为 150 m 和 200 m,AB=250 m,大型工程车周围 130 m 以内为受噪声影响区域.
(1)学校 C 会受噪声影响吗?为什么?
B
A
C
(2)若大型工程车的行驶速度为 50 m/min,
大型工程车噪声影响该学校持续的时间
有多少分钟?
典例精析
例6
解:学校 C 会受噪声影响.
理由:如图,过点 C 作 CD⊥AB 于 D,
∵AC=150 m,BC=200 m,AB=250 m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∴S△ABC= AC·BC= CD·AB,
∴150×200=250CD,
∴CD= =120(m),
∵大型工程车周围 130 m 以内为受噪声影响区域,
∴学校 C 会受噪声影响.
A
B
C
D
典例精析
例6
∴EF=100(m).
(2)如图,取 EC=130 m,FC=130 m,当大型工程车在 EF 上时学校会受
噪声影响.
∵ED2=EC2-CD2=1302-1202=502,
∴ED=50(m),
∵大型工程车的行驶速度为 50 m/min,
∴100÷50=2(min),
即大型工程车噪声影响该学校持续的时间有 2 min.
E
F
A
B
C
D
典例精析
例7
锐角
钝角
>
<
典例精析
例7
归纳总结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
当堂检测
1.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
D
当堂检测
2.如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,AD= .
若AC⊥BC,求证:AD∥BC.
∴AD∥BC
当堂检测
3.如图,某中学为迎接校庆50周年,拟对学校校园中的一块空地进行美化
施工,已知AB=3 m,BC=4 m,∠ABC=90°,AD=12 m,CD=13 m,
学校欲在此空地上铺草坪,已知每平方米草坪80元,试问用草坪铺满这
块空地共需花费多少元.
解:如图,连接AC,在Rt△ABC中,
∵AC2=AB2+BC2=32+42=25,
∴AC=5 m.
∵AC2+AD2=52+122=169,CD2=132=169,
∴AC2+AD2=CD2,∴∠CAD=90°,
该区域面积=S△ACD-S△ABC=30-6=24(m2),
铺满这块空地共需花费24×80=1 920(元).
答:用草坪铺满这块空地共需花费1 920元.
当堂检测
A
B
C
D
M
N
北
东
4.一艘轮船从 A 港向南偏西 48°方向航行 100 km 到达 B 岛,再从 B 岛沿 BM 方向航行 125 km 到达 C 岛,A 港到航线 BM 的最短距离是 60 km.
(1)若轮船速度为 25 km/h,求轮船从 C 岛沿 CA 方向返回 A 港所需的时间;
∴ (km).
解:(1)由题意 AD=60 km,
在 Rt△ABD 中,由 AD2+BD2=AB2 得 602+BD2=1002.
∴BD=80(km).
∴CD=BC-BD=125-80=45(km).
75÷25=3(h).
答:从 C 岛沿 CA 方向返回 A 港所需的时间为 3 h.
当堂检测
(2)C 岛在 A 港的什么方向?
解:(2)∵AB2+AC2=1002+752=15 625,
BC2=1252=15 625,
∴AB2+AC2=BC2,
∴∠BAC=90°.
∴∠NAC=180°-90°-48°=42°.
∴C 岛在 A 港的北偏西 42°方向上.
A
B
C
D
M
N
北
东
