华东师大版(2012)数学八年级下册第十九章矩形、菱形与正方形章节拔高练习(含答案)
文档属性
| 名称 | 华东师大版(2012)数学八年级下册第十九章矩形、菱形与正方形章节拔高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 539.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 10:59:19 | ||
图片预览



文档简介
华东师大版(2012)数学八年级下册第十九章矩形、菱形与正方形章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
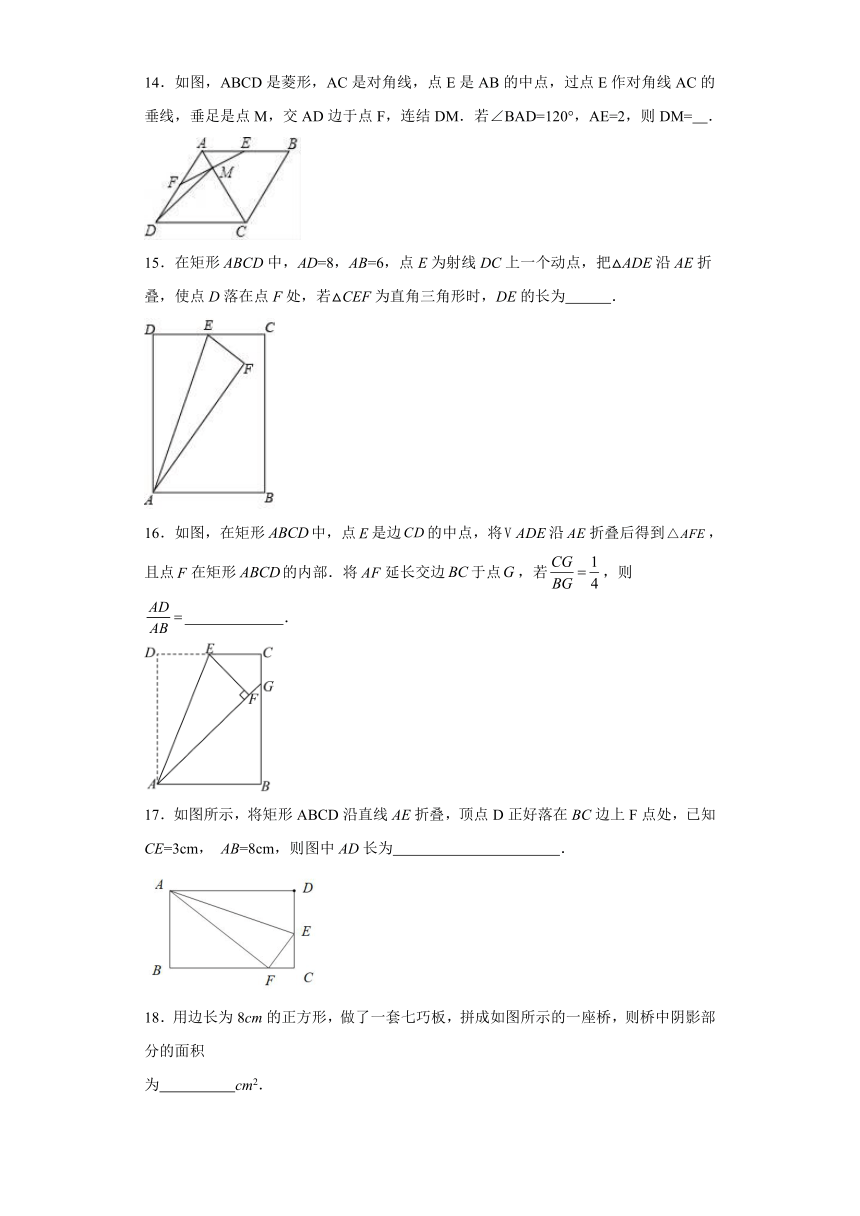
1.如图所示,在矩形中,,,矩形内部有一动点满足,则点到,两点的距离之和的最小值为( ).
A. B. C. D.
2.如图,正方形ABCD四边的中点分别是E、F、G、H,若四边形EFGH的面积是2,则正方形ABCD的周长是( )
A.4 B.4 C.8 D.8
3.如图,正方形在平面直角坐标系中的点A和点B的坐标为、,点D在双曲线上.若正方形沿x轴负方向平移m个单位长度后,点C恰好落在该双曲线上,则m的值是( )
A.2 B.3 C.4 D.5
4.下列命题中不正确的是( )
A.斜边对应相等的两个等腰直角三角形全等
B.有两条直角边对应相等的两个直角三角形全等
C.有一条边相等的两个等腰三角形全等
D.有一条直角边和斜边上的中线对应相等的两个直角三角形全等
5.如图,正方形的面积是,E、F、P分别是AB、BC、AC上的动点,的最小值等于( )
A.5 B. C. D.
6.如图,在菱形中,对角线 相交于点为 的中点,且,则菱形 的周长为( )
A. B. C. D.
7.下列图形对称轴最多的是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8.矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于( )
A.16 B.8 C.16 D.8
9.正方形,,按如图的方式放置,和点分别在直线和x轴上,则点的坐标是( )
A. B. C. D.
10.下列命题中,假命题是( )
A.矩形的对角线相等 B.矩形对角线交点到四个顶点的距离相等
C.矩形的对角线互相平分 D.矩形对角线交点到四条边的距离相等
二、填空题
11.如图,在等腰三角形纸片中,,,沿底边上的高剪成两个三角形,用这两个三角形拼成平行四边形,则能够拼出的平行四边形对角线长度最大值为 .
12.如图,E,F是矩形ABCD的边AD和BC上的两点,连接BE,DF,BD,请添加一个适当的条件,使△BED≌△DFB, (填一个即可).
13.如图,将矩形ABCD沿EF折叠,使点B落在点D处,点A落在点G处,若AB=4,BC=2AB,则线段DE的长为 .
14.如图,ABCD是菱形,AC是对角线,点E是AB的中点,过点E作对角线AC的垂线,垂足是点M,交AD边于点F,连结DM.若∠BAD=120°,AE=2,则DM= .
15.在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为 .
16.如图,在矩形中,点是边的中点,将沿折叠后得到,且点在矩形的内部.将延长交边于点,若,则 .
17.如图所示,将矩形ABCD沿直线AE折叠,顶点D正好落在BC边上F点处,已知CE=3cm, AB=8cm,则图中AD长为 .
18.用边长为8cm的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积
为 cm2.
19.如图,边长为5的菱形ABCD中,对角线AC长为6,菱形的面积为 .
20.如图,在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4,则对角线BD的长为
三、解答题
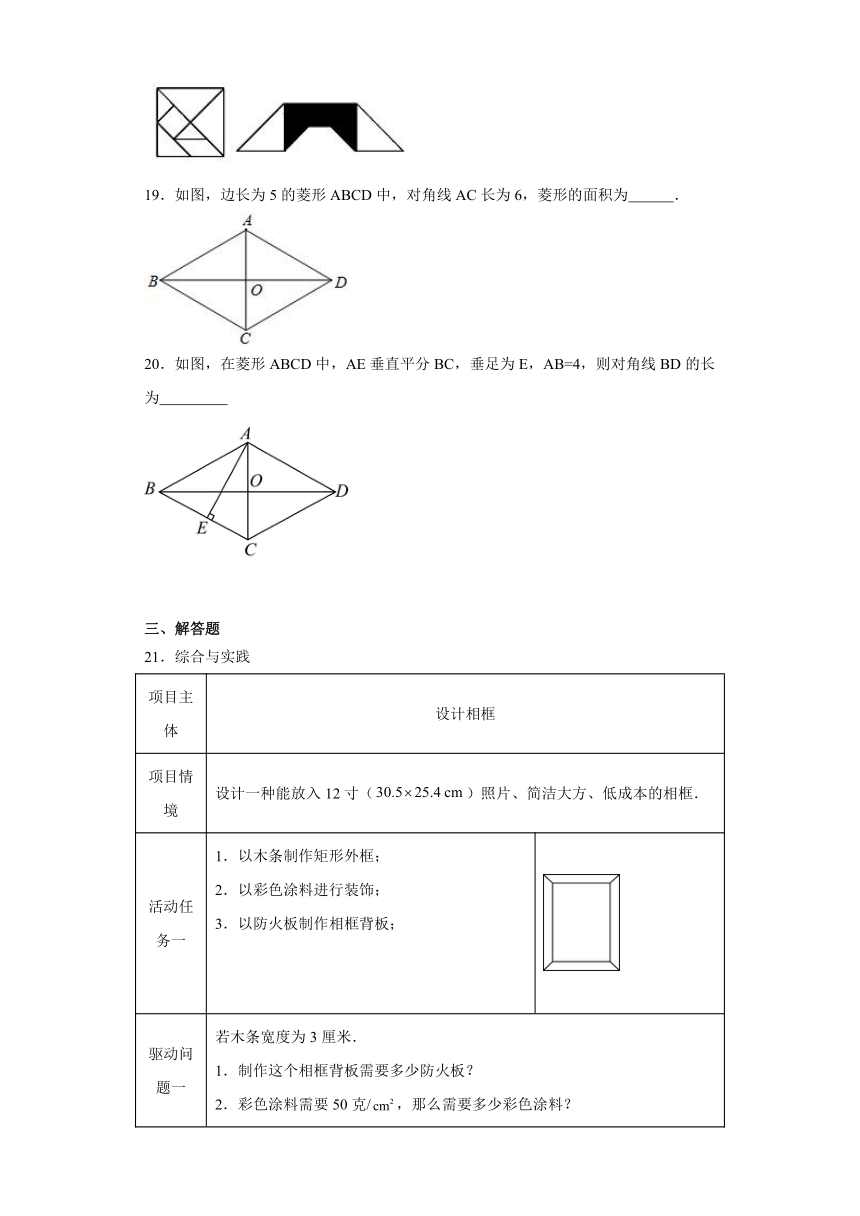
21.综合与实践
项目主体 设计相框
项目情境 设计一种能放入12寸()照片、简洁大方、低成本的相框.
活动任务一 1.以木条制作矩形外框; 2.以彩色涂料进行装饰; 3.以防火板制作相框背板;
驱动问题一 若木条宽度为3厘米. 1.制作这个相框背板需要多少防火板? 2.彩色涂料需要50克/,那么需要多少彩色涂料?
活动任务二 运用所学的函数知识,通过函数图象探究当相框的面积为4时,相框面积与周长的关系.
驱动问题二 3.设相框的长为x、宽为y,则,时,用图象的观点解析满足要求的的意义?
22.问题探究
(1)如图①,在四边形中,,,,,则的面积________.
(2)如图②,在中,点A是平面内一动点,且始终满足,,求的最小值.
(3)如图③,四边形为公园中的一片花圃,现计划在四边形内找一点P,连接,使得将四边形分成面积相等的两部分,分别用于种植两种不同品种的花,同时沿着修一条观赏的道路.为了降低成本,公园管理人员希望的和最小.以B为坐标原点,BC所在直线为x轴,建立如图③所示的平面直角坐标系,根据测量的数据可得:,,,请探究是否存在满足要求的点P,若存在,请在图中作出点P,并求出点P的坐标;若不存在,说明理由
23.如图所示,点为正方形的对角线的交点,若点在正方形内部时,且.试探究,,之间的数量关系.
24.如图,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
25.在边长为6的菱形中,,点E、F是边、上的点,连接.
(1)如图1,将沿翻折使B的对应点落在中点上,此时四边形是什么四边形?并说明理由.
(2)如图2,若,以为边在右侧作等边;
①连接,当是以为腰的等腰三角形时,求的长度.
②直接写出的最小值.
26.在平面直角坐标系中,点A(0,a),点B(b,0),其中参数a、b满足如下关系式|2a﹣b|+(6﹣b)2=0.
(1)直接写出A、B两点坐标:A 、B .
(2)如图1,C点的横坐标为3,且AC平分∠BAy,作CD⊥AB于D,求BD﹣AD的值;
(3)如图2,现以AB为斜边构造等腰直角三角形ABM,试求以A、B、O、M为顶点的四边形的面积.
27.如图,在矩形中,对角线,相交于点O,垂直平分,交于点E,交于点F,连接,若,求的长.
参考答案:
1.D
2.C
3.C
4.C
5.C
6.C
7.C
8.D
9.A
10.D
11.
12.ED=FB(答案不唯一)
13.5
14..
15.或8或或
16.
17.10 cm
18.32
19.24
20.
21.(1)(2)18570克(3)为反比例函数与一次函数的图象的交点.
22.(1)
(2);
(3).
23.
24.(1)3;(2)(7,4);(3)存在,(﹣2,)或(,)
25.(1)菱形,(2)①或3;②.
26.(1);(2)3;(3)或
27.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,在矩形中,,,矩形内部有一动点满足,则点到,两点的距离之和的最小值为( ).
A. B. C. D.
2.如图,正方形ABCD四边的中点分别是E、F、G、H,若四边形EFGH的面积是2,则正方形ABCD的周长是( )
A.4 B.4 C.8 D.8
3.如图,正方形在平面直角坐标系中的点A和点B的坐标为、,点D在双曲线上.若正方形沿x轴负方向平移m个单位长度后,点C恰好落在该双曲线上,则m的值是( )
A.2 B.3 C.4 D.5
4.下列命题中不正确的是( )
A.斜边对应相等的两个等腰直角三角形全等
B.有两条直角边对应相等的两个直角三角形全等
C.有一条边相等的两个等腰三角形全等
D.有一条直角边和斜边上的中线对应相等的两个直角三角形全等
5.如图,正方形的面积是,E、F、P分别是AB、BC、AC上的动点,的最小值等于( )
A.5 B. C. D.
6.如图,在菱形中,对角线 相交于点为 的中点,且,则菱形 的周长为( )
A. B. C. D.
7.下列图形对称轴最多的是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8.矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于( )
A.16 B.8 C.16 D.8
9.正方形,,按如图的方式放置,和点分别在直线和x轴上,则点的坐标是( )
A. B. C. D.
10.下列命题中,假命题是( )
A.矩形的对角线相等 B.矩形对角线交点到四个顶点的距离相等
C.矩形的对角线互相平分 D.矩形对角线交点到四条边的距离相等
二、填空题
11.如图,在等腰三角形纸片中,,,沿底边上的高剪成两个三角形,用这两个三角形拼成平行四边形,则能够拼出的平行四边形对角线长度最大值为 .
12.如图,E,F是矩形ABCD的边AD和BC上的两点,连接BE,DF,BD,请添加一个适当的条件,使△BED≌△DFB, (填一个即可).
13.如图,将矩形ABCD沿EF折叠,使点B落在点D处,点A落在点G处,若AB=4,BC=2AB,则线段DE的长为 .
14.如图,ABCD是菱形,AC是对角线,点E是AB的中点,过点E作对角线AC的垂线,垂足是点M,交AD边于点F,连结DM.若∠BAD=120°,AE=2,则DM= .
15.在矩形ABCD中,AD=8,AB=6,点E为射线DC上一个动点,把△ADE沿AE折叠,使点D落在点F处,若△CEF为直角三角形时,DE的长为 .
16.如图,在矩形中,点是边的中点,将沿折叠后得到,且点在矩形的内部.将延长交边于点,若,则 .
17.如图所示,将矩形ABCD沿直线AE折叠,顶点D正好落在BC边上F点处,已知CE=3cm, AB=8cm,则图中AD长为 .
18.用边长为8cm的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积
为 cm2.
19.如图,边长为5的菱形ABCD中,对角线AC长为6,菱形的面积为 .
20.如图,在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4,则对角线BD的长为
三、解答题
21.综合与实践
项目主体 设计相框
项目情境 设计一种能放入12寸()照片、简洁大方、低成本的相框.
活动任务一 1.以木条制作矩形外框; 2.以彩色涂料进行装饰; 3.以防火板制作相框背板;
驱动问题一 若木条宽度为3厘米. 1.制作这个相框背板需要多少防火板? 2.彩色涂料需要50克/,那么需要多少彩色涂料?
活动任务二 运用所学的函数知识,通过函数图象探究当相框的面积为4时,相框面积与周长的关系.
驱动问题二 3.设相框的长为x、宽为y,则,时,用图象的观点解析满足要求的的意义?
22.问题探究
(1)如图①,在四边形中,,,,,则的面积________.
(2)如图②,在中,点A是平面内一动点,且始终满足,,求的最小值.
(3)如图③,四边形为公园中的一片花圃,现计划在四边形内找一点P,连接,使得将四边形分成面积相等的两部分,分别用于种植两种不同品种的花,同时沿着修一条观赏的道路.为了降低成本,公园管理人员希望的和最小.以B为坐标原点,BC所在直线为x轴,建立如图③所示的平面直角坐标系,根据测量的数据可得:,,,请探究是否存在满足要求的点P,若存在,请在图中作出点P,并求出点P的坐标;若不存在,说明理由
23.如图所示,点为正方形的对角线的交点,若点在正方形内部时,且.试探究,,之间的数量关系.
24.如图,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
25.在边长为6的菱形中,,点E、F是边、上的点,连接.
(1)如图1,将沿翻折使B的对应点落在中点上,此时四边形是什么四边形?并说明理由.
(2)如图2,若,以为边在右侧作等边;
①连接,当是以为腰的等腰三角形时,求的长度.
②直接写出的最小值.
26.在平面直角坐标系中,点A(0,a),点B(b,0),其中参数a、b满足如下关系式|2a﹣b|+(6﹣b)2=0.
(1)直接写出A、B两点坐标:A 、B .
(2)如图1,C点的横坐标为3,且AC平分∠BAy,作CD⊥AB于D,求BD﹣AD的值;
(3)如图2,现以AB为斜边构造等腰直角三角形ABM,试求以A、B、O、M为顶点的四边形的面积.
27.如图,在矩形中,对角线,相交于点O,垂直平分,交于点E,交于点F,连接,若,求的长.
参考答案:
1.D
2.C
3.C
4.C
5.C
6.C
7.C
8.D
9.A
10.D
11.
12.ED=FB(答案不唯一)
13.5
14..
15.或8或或
16.
17.10 cm
18.32
19.24
20.
21.(1)(2)18570克(3)为反比例函数与一次函数的图象的交点.
22.(1)
(2);
(3).
23.
24.(1)3;(2)(7,4);(3)存在,(﹣2,)或(,)
25.(1)菱形,(2)①或3;②.
26.(1);(2)3;(3)或
27.
