江西省上饶市重点中学2023-2024学年八年级下学期开学考试数学试题(无答案)
文档属性
| 名称 | 江西省上饶市重点中学2023-2024学年八年级下学期开学考试数学试题(无答案) | 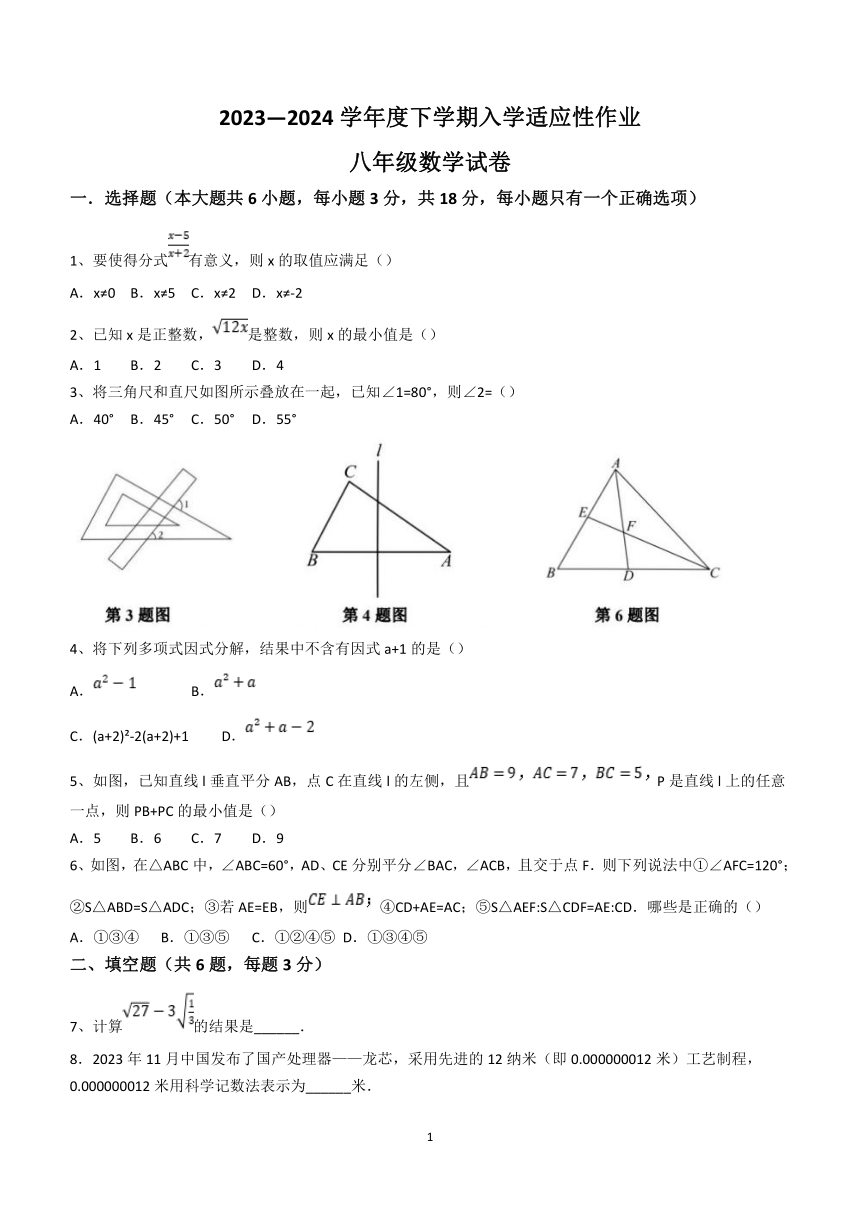 | |
| 格式 | doc | ||
| 文件大小 | 489.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:51:32 | ||
图片预览


文档简介
2023—2024学年度下学期入学适应性作业
八年级数学试卷
一.选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)
1、要使得分式有意义,则x的取值应满足()
A.x≠0 B.x≠5 C.x≠2 D.x≠-2
2、已知x是正整数,是整数,则x的最小值是()
A.1 B.2 C.3 D.4
3、将三角尺和直尺如图所示叠放在一起,已知∠1=80°,则∠2=()
A.40° B.45° C.50° D.55°
4、将下列多项式因式分解,结果中不含有因式a+1的是()
A. B.
C.(a+2) -2(a+2)+1 D.
5、如图,已知直线l垂直平分AB,点C在直线l的左侧,且P是直线l上的任意一点,则PB+PC的最小值是()
A.5 B.6 C.7 D.9
6、如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,且交于点F.则下列说法中①∠AFC=120°;②S△ABD=S△ADC;③若AE=EB,则④CD+AE=AC;⑤S△AEF:S△CDF=AE:CD.哪些是正确的()
A.①③④ B.①③⑤ C.①②④⑤ D.①③④⑤
二、填空题(共6题,每题3分)
7、计算的结果是______.
8.2023年11月中国发布了国产处理器——龙芯,采用先进的12纳米(即0.000000012米)工艺制程,0.000000012米用科学记数法表示为______米.
9.若a,b满足则点(a,b)在第______象限.
10.已知则______.
11、如图,已知方格纸中是4个相同的小正方形,则的度数为______.
12、如图,有一个三角形纸片ABC,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则的度数可以是______.
三.解答题(共5题,每题6分)
13、计算:
(1); (2)
14、一个正多边形的一个外角等于它的一个内角的则这个正多形是几边形?
15、先化简,再求值:其中.
16、如图所示,点C,E分别为的边BD,AB上两点,且求∠B的度数.
17、如图,在正六边形ABCDEF中,连接BD,请用无刻度的直尺,完成下列作图
(1)如图①,作出一个边长等于BD的等边三角形;
(2)如图②,作出一个周长等于BD的等边三角形.
四.解答题(共3题,每题8分)
18、小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:.
(1)她把这个数“?”猜成5,请你帮小华解这个分式方程.
(2)小华的妈妈说:“我看到标准答案是:原分式方程无解.”请你求出原分式方程中“?”代表的数是多少.
19、如图,在中,点D,E分别在边AB,AC上,连结CD,BE.
(1)若求的度数;
(2)写出.与之间的关系,并说明理由.
20、请阅读下列材料:
问题:已知求代数式的值.
小敏的做法是:根据得(
得:
把作为整体代入:得
即:把已知条件适当变形,再整体代入解决问题.请你用上述方法解决下面问题:
(1)己知:求代数式的值;
(2)已知求代数式的值.
五.解答题(共2题,每题9分)
21、(1)如图1,在△ABC中,AB=AC,点D是AC边上一点,连接BD,G,F两点都在线段BD上,连接AG,AF,过C作CE∥BD交AF延长线于点E,若AG=AF,∠ABD=∠CAE.求证:AG=CE;
(2)如图2,在△ABC中,AB=AC,点D为△ABC下方一点,连接AD,BD,过C作CE∥BD交AD于点E,若∠ABD=∠CAE,CE=3,AE=1,求DE的长.
22、对于代数式,不同的表达形式能表现出它不同的性质,若代数式代数式改变x的值,代数式A,B有不同的取值,如下表:
x -1 0 1 2 3 4
A=x +4x+3 0 3 8 15 24 35
B=(x-1) +4(x-1)+3 -1 0 3 8 15 24
观察表格发现:当x=m时,当x=m+1时,4(x-1)+3=n,我们把这种现象称为代数式B参照代数式A取值延后,相应的延后值为1.
(1)若代数式D参照代数式A取值延后,相应的延后值为2,求代数式D;
(2)若代数式参照代数式A的取值延后,求相应的延后值;
(3)若代数式参照代数式(取值延后,求b-c的值.
六.解答题(共1题,12分)
23、已知:在平面直角坐标系中,A(0,a),B(b,0),且a,b满足点C在x轴正半轴,(动点P从点B出发,以1个单位长度/秒的速度沿x轴向点C运动,运动到点C停止,设点P的运动时间为t秒,连接AP,过点C作AP的垂线交射线AP于点交M,交y轴于N.
(1)点A的坐标为,点B的坐标为.
(2)当点P在线段OB上时,如图②所示,求线段ON的长度(用含t的式子表示).
(3)若则t的值为.
(4)若是否存在以AB为腰的等腰三角形ABP?若存在,请直接写出点P的坐标;若不存在,请说明理由.
八年级数学试卷
一.选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)
1、要使得分式有意义,则x的取值应满足()
A.x≠0 B.x≠5 C.x≠2 D.x≠-2
2、已知x是正整数,是整数,则x的最小值是()
A.1 B.2 C.3 D.4
3、将三角尺和直尺如图所示叠放在一起,已知∠1=80°,则∠2=()
A.40° B.45° C.50° D.55°
4、将下列多项式因式分解,结果中不含有因式a+1的是()
A. B.
C.(a+2) -2(a+2)+1 D.
5、如图,已知直线l垂直平分AB,点C在直线l的左侧,且P是直线l上的任意一点,则PB+PC的最小值是()
A.5 B.6 C.7 D.9
6、如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC,∠ACB,且交于点F.则下列说法中①∠AFC=120°;②S△ABD=S△ADC;③若AE=EB,则④CD+AE=AC;⑤S△AEF:S△CDF=AE:CD.哪些是正确的()
A.①③④ B.①③⑤ C.①②④⑤ D.①③④⑤
二、填空题(共6题,每题3分)
7、计算的结果是______.
8.2023年11月中国发布了国产处理器——龙芯,采用先进的12纳米(即0.000000012米)工艺制程,0.000000012米用科学记数法表示为______米.
9.若a,b满足则点(a,b)在第______象限.
10.已知则______.
11、如图,已知方格纸中是4个相同的小正方形,则的度数为______.
12、如图,有一个三角形纸片ABC,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则的度数可以是______.
三.解答题(共5题,每题6分)
13、计算:
(1); (2)
14、一个正多边形的一个外角等于它的一个内角的则这个正多形是几边形?
15、先化简,再求值:其中.
16、如图所示,点C,E分别为的边BD,AB上两点,且求∠B的度数.
17、如图,在正六边形ABCDEF中,连接BD,请用无刻度的直尺,完成下列作图
(1)如图①,作出一个边长等于BD的等边三角形;
(2)如图②,作出一个周长等于BD的等边三角形.
四.解答题(共3题,每题8分)
18、小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:.
(1)她把这个数“?”猜成5,请你帮小华解这个分式方程.
(2)小华的妈妈说:“我看到标准答案是:原分式方程无解.”请你求出原分式方程中“?”代表的数是多少.
19、如图,在中,点D,E分别在边AB,AC上,连结CD,BE.
(1)若求的度数;
(2)写出.与之间的关系,并说明理由.
20、请阅读下列材料:
问题:已知求代数式的值.
小敏的做法是:根据得(
得:
把作为整体代入:得
即:把已知条件适当变形,再整体代入解决问题.请你用上述方法解决下面问题:
(1)己知:求代数式的值;
(2)已知求代数式的值.
五.解答题(共2题,每题9分)
21、(1)如图1,在△ABC中,AB=AC,点D是AC边上一点,连接BD,G,F两点都在线段BD上,连接AG,AF,过C作CE∥BD交AF延长线于点E,若AG=AF,∠ABD=∠CAE.求证:AG=CE;
(2)如图2,在△ABC中,AB=AC,点D为△ABC下方一点,连接AD,BD,过C作CE∥BD交AD于点E,若∠ABD=∠CAE,CE=3,AE=1,求DE的长.
22、对于代数式,不同的表达形式能表现出它不同的性质,若代数式代数式改变x的值,代数式A,B有不同的取值,如下表:
x -1 0 1 2 3 4
A=x +4x+3 0 3 8 15 24 35
B=(x-1) +4(x-1)+3 -1 0 3 8 15 24
观察表格发现:当x=m时,当x=m+1时,4(x-1)+3=n,我们把这种现象称为代数式B参照代数式A取值延后,相应的延后值为1.
(1)若代数式D参照代数式A取值延后,相应的延后值为2,求代数式D;
(2)若代数式参照代数式A的取值延后,求相应的延后值;
(3)若代数式参照代数式(取值延后,求b-c的值.
六.解答题(共1题,12分)
23、已知:在平面直角坐标系中,A(0,a),B(b,0),且a,b满足点C在x轴正半轴,(动点P从点B出发,以1个单位长度/秒的速度沿x轴向点C运动,运动到点C停止,设点P的运动时间为t秒,连接AP,过点C作AP的垂线交射线AP于点交M,交y轴于N.
(1)点A的坐标为,点B的坐标为.
(2)当点P在线段OB上时,如图②所示,求线段ON的长度(用含t的式子表示).
(3)若则t的值为.
(4)若是否存在以AB为腰的等腰三角形ABP?若存在,请直接写出点P的坐标;若不存在,请说明理由.
同课章节目录
