2023-2024学年初中数学人教版八年级下册第十八章平行四边形复习课 课时练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册第十八章平行四边形复习课 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 116.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 14:41:00 | ||
图片预览


文档简介
第十八章 复习课
【基础作业】
1.下列说法不正确的是 ( )
A.两组对边分别相等的四边形是平行四边形
B.一个角是直角的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.对角线相等的四边形是矩形
2.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB=90°,D为边AB的中点,点A,B对应的刻度分别为1,7,则CD的长为 ( )
A.3.5 cm B.3 cm
C.4.5 cm D.6 cm
3.将一个正方形纸片折叠一次,使得左右两边完全重合,则这样的折痕可以有 ( )
A.0条 B.2条 C.4条 D.6条
4.矩形的一个内角平分线把矩形的一边分成3和5,则矩形的周长为 ( )
A.16 B.16或22
C.22或26 D.以上都不对
5.如图,D,E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE=BC.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,∴四边形ADCF是平行四边形,
接着以下是排序错误的证明过程:
①∴DF BC;
②∴CF AD,即CF BD;
③∴四边形DBCF是平行四边形;
④∴DE∥BC,且DE=BC.
则正确的证明顺序应是 ( )
A.①→③→②→④
B.①→③→④→②
C.②→③→①→④
D.②→③→④→①
6.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
7.如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
【巩固作业】
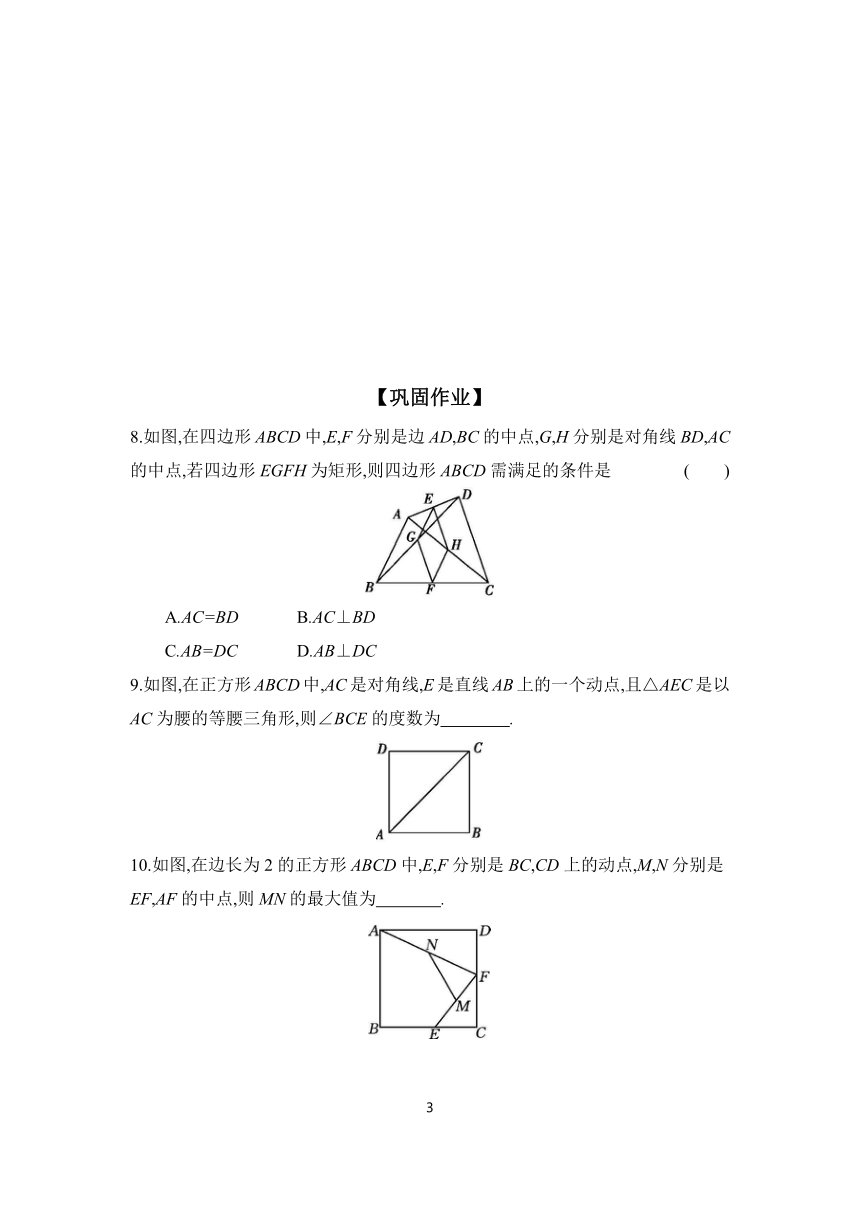
8.如图,在四边形ABCD中,E,F分别是边AD,BC的中点,G,H分别是对角线BD,AC的中点,若四边形EGFH为矩形,则四边形ABCD需满足的条件是 ( )
A.AC=BD B.AC⊥BD
C.AB=DC D.AB⊥DC
9.如图,在正方形ABCD中,AC是对角线,E是直线AB上的一个动点,且△AEC是以AC为腰的等腰三角形,则∠BCE的度数为 .
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
11.如图,在正方形ABCD中,E是对角线BD上一点,且不与B,D两点重合,F是直线CB上一点,且EF=EC.
(1)求证:AE=EF.
(2)若BE=AB,请在图2中补全图形,判断AF与EC的数量关系并加以证明.
【素养作业】
12.如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P,Q的速度都是每秒1个单位长度,连接PQ,AQ,CP.设点P,Q运动的时间为t秒.
(1)当t为何值时,四边形ABQP是矩形
(2)当t=6时,判断四边形AQCP的形状,并说明理由.
参考答案
1.D 2.B 3.C 4.C 5.C 6.36°
7.证明:(1)在 ABCD中,OA=OC,OB=OD.
∵AE=CF,∴OE=OF,
∴四边形EBFD是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,∴∠BAC=∠DCA.
∵∠BAC=∠DAC,∴∠DCA=∠DAC,
∴DA=DC,
∴平行四边形ABCD为菱形,∴DB⊥EF,
∴四边形EBFD是菱形.
8.D 9.67.5°或22.5°或45°
10.
提示:如图,连接AE.
∵M,N分别是EF,AF的中点,
∴MN是△AEF的中位线,
∴MN=AE.
∵四边形ABCD是正方形,∠B=90°,
∴AE==,
∴当BE最大时,AE最大,此时MN最大.
∵E是BC上的动点,
∴当点E和点C重合时,BE最大,即BC的长度,
∴此时AE==2,
MN=AE=,∴MN的最大值为.
故答案为.
11.解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ADB=∠CDB=45°.
在△ADE与△CDE中,
∴△ADE≌△CDE(SAS),∴AE=CE.
∵EF=EC,∴AE=EF.
(2)补全图形如图所示.AF=CE.
证明:∵AB=BE=BC,∠ABD=∠DBC=45°,
∴∠BAE=∠AEB=∠BEC=∠BCE=67.5°.
∵EF=EC,∴∠EFC=∠ECF=67.5°,∴∠FEC=45°,∠BFE=112.5°.
∵∠BAE+∠AEF+∠BFE+∠ABF=360°,
∴∠AEF=90°,且AE=EF,∴∠AFE=45°,
∴∠AFE=∠FEC=45°,∴AF=EF,
∴AF=CE.
12.解:(1)∵在矩形ABCD中,AB=8,BC=16,
∴BC=AD=16,AB=CD=8.
由已知可得BQ=DP=t,AP=CQ=16-t,
在矩形ABCD中,∠B=90°,AD∥BC,
当BQ=AP时,四边形ABQP为矩形,
∴t=16-t,解得t=8,
∴当t=8时,四边形ABQP为矩形.
(2)四边形AQCP为菱形.
理由:∵t=6,∴BQ=6,DP=6,
∴CQ=16-6=10,AP=16-6=10,
∴AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形.
在Rt△ABQ中,AQ===10,∴AQ=CQ,
∴平行四边形AQCP为菱形,
即当t=6时,四边形AQCP为菱形
2
【基础作业】
1.下列说法不正确的是 ( )
A.两组对边分别相等的四边形是平行四边形
B.一个角是直角的平行四边形是矩形
C.对角线互相平分且垂直的四边形是菱形
D.对角线相等的四边形是矩形
2.一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图,已知∠ACB=90°,D为边AB的中点,点A,B对应的刻度分别为1,7,则CD的长为 ( )
A.3.5 cm B.3 cm
C.4.5 cm D.6 cm
3.将一个正方形纸片折叠一次,使得左右两边完全重合,则这样的折痕可以有 ( )
A.0条 B.2条 C.4条 D.6条
4.矩形的一个内角平分线把矩形的一边分成3和5,则矩形的周长为 ( )
A.16 B.16或22
C.22或26 D.以上都不对
5.如图,D,E分别是△ABC的边AB,AC的中点.
求证:DE∥BC,且DE=BC.
证明:如图,延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,∴四边形ADCF是平行四边形,
接着以下是排序错误的证明过程:
①∴DF BC;
②∴CF AD,即CF BD;
③∴四边形DBCF是平行四边形;
④∴DE∥BC,且DE=BC.
则正确的证明顺序应是 ( )
A.①→③→②→④
B.①→③→④→②
C.②→③→①→④
D.②→③→④→①
6.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
7.如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(1)求证:四边形EBFD是平行四边形.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
【巩固作业】
8.如图,在四边形ABCD中,E,F分别是边AD,BC的中点,G,H分别是对角线BD,AC的中点,若四边形EGFH为矩形,则四边形ABCD需满足的条件是 ( )
A.AC=BD B.AC⊥BD
C.AB=DC D.AB⊥DC
9.如图,在正方形ABCD中,AC是对角线,E是直线AB上的一个动点,且△AEC是以AC为腰的等腰三角形,则∠BCE的度数为 .
10.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
11.如图,在正方形ABCD中,E是对角线BD上一点,且不与B,D两点重合,F是直线CB上一点,且EF=EC.
(1)求证:AE=EF.
(2)若BE=AB,请在图2中补全图形,判断AF与EC的数量关系并加以证明.
【素养作业】
12.如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P,Q的速度都是每秒1个单位长度,连接PQ,AQ,CP.设点P,Q运动的时间为t秒.
(1)当t为何值时,四边形ABQP是矩形
(2)当t=6时,判断四边形AQCP的形状,并说明理由.
参考答案
1.D 2.B 3.C 4.C 5.C 6.36°
7.证明:(1)在 ABCD中,OA=OC,OB=OD.
∵AE=CF,∴OE=OF,
∴四边形EBFD是平行四边形.
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,∴∠BAC=∠DCA.
∵∠BAC=∠DAC,∴∠DCA=∠DAC,
∴DA=DC,
∴平行四边形ABCD为菱形,∴DB⊥EF,
∴四边形EBFD是菱形.
8.D 9.67.5°或22.5°或45°
10.
提示:如图,连接AE.
∵M,N分别是EF,AF的中点,
∴MN是△AEF的中位线,
∴MN=AE.
∵四边形ABCD是正方形,∠B=90°,
∴AE==,
∴当BE最大时,AE最大,此时MN最大.
∵E是BC上的动点,
∴当点E和点C重合时,BE最大,即BC的长度,
∴此时AE==2,
MN=AE=,∴MN的最大值为.
故答案为.
11.解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ADB=∠CDB=45°.
在△ADE与△CDE中,
∴△ADE≌△CDE(SAS),∴AE=CE.
∵EF=EC,∴AE=EF.
(2)补全图形如图所示.AF=CE.
证明:∵AB=BE=BC,∠ABD=∠DBC=45°,
∴∠BAE=∠AEB=∠BEC=∠BCE=67.5°.
∵EF=EC,∴∠EFC=∠ECF=67.5°,∴∠FEC=45°,∠BFE=112.5°.
∵∠BAE+∠AEF+∠BFE+∠ABF=360°,
∴∠AEF=90°,且AE=EF,∴∠AFE=45°,
∴∠AFE=∠FEC=45°,∴AF=EF,
∴AF=CE.
12.解:(1)∵在矩形ABCD中,AB=8,BC=16,
∴BC=AD=16,AB=CD=8.
由已知可得BQ=DP=t,AP=CQ=16-t,
在矩形ABCD中,∠B=90°,AD∥BC,
当BQ=AP时,四边形ABQP为矩形,
∴t=16-t,解得t=8,
∴当t=8时,四边形ABQP为矩形.
(2)四边形AQCP为菱形.
理由:∵t=6,∴BQ=6,DP=6,
∴CQ=16-6=10,AP=16-6=10,
∴AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形.
在Rt△ABQ中,AQ===10,∴AQ=CQ,
∴平行四边形AQCP为菱形,
即当t=6时,四边形AQCP为菱形
2
