第十九章 一次函数复习课 课时练习 (含答案)2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 第十九章 一次函数复习课 课时练习 (含答案)2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 165.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 14:41:56 | ||
图片预览



文档简介
第十九章 复习课
【基础作业】
1.有下列函数:①y=2x;②y=;③y=2x+1;④y=2x2+1.其中y是关于x的一次函数有 ( )
A.1个 B.2个
C.3个 D.4个
2.在函数y=中,自变量x的取值范围是 ( )
A.x≥1 B.x>2
C.x≥1且x≠2 D.x≠2
3.如图,这是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是 ( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
4.将直线y=3x向下平移3个单位长度后所得直线的解析式是 .
5.如图,已知一次函数y=kx+b,观察图象回答下列问题:当x 时,kx+b>0;当x 时,kx+b<1.
【巩固作业】
6.甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(单位:km)与行驶时间t(单位:h)的函数图象如图所示,下列说法正确的有 ( )
①甲车的速度为50 km/h;②乙车用了3 h到达B城;③甲车出发4 h时,乙车追上甲车.
A.0个 B.1个 C.2个 D.3个
7.若点M(k-1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k-1)x+k的图象不经过第 象限.
8.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(单位:km)与甲车行驶时间t(单位:h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.
9.已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所有可能取得的整数值为 .
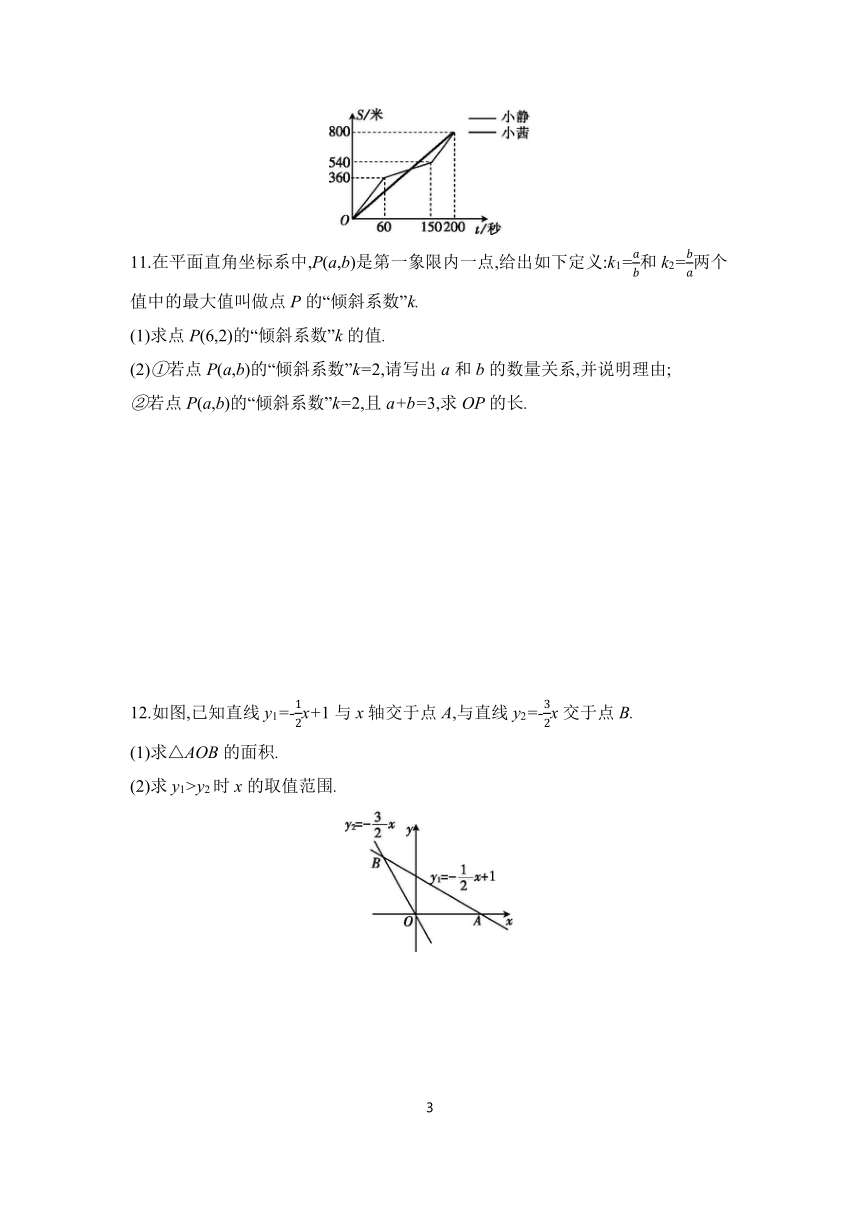
10.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 秒.
11.在平面直角坐标系中,P(a,b)是第一象限内一点,给出如下定义:k1=和k2=两个值中的最大值叫做点P的“倾斜系数”k.
(1)求点P(6,2)的“倾斜系数”k的值.
(2)①若点P(a,b)的“倾斜系数”k=2,请写出a和b的数量关系,并说明理由;
②若点P(a,b)的“倾斜系数”k=2,且a+b=3,求OP的长.
12.如图,已知直线y1=-x+1与x轴交于点A,与直线y2=-x交于点B.
(1)求△AOB的面积.
(2)求y1>y2时x的取值范围.
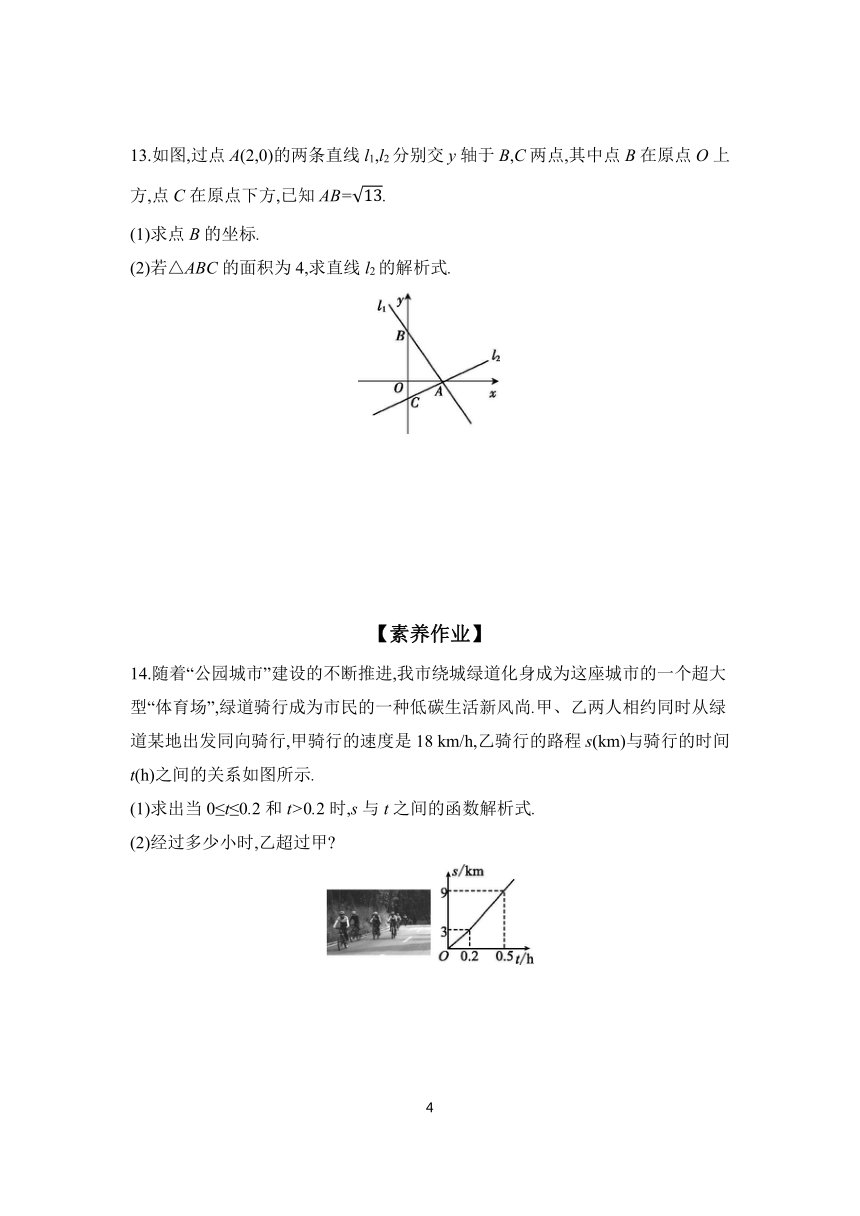
13.如图,过点A(2,0)的两条直线l1,l2分别交y轴于B,C两点,其中点B在原点O上方,点C在原点下方,已知AB=.
(1)求点B的坐标.
(2)若△ABC的面积为4,求直线l2的解析式.
【素养作业】
14.随着“公园城市”建设的不断推进,我市绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是18 km/h,乙骑行的路程s(km)与骑行的时间t(h)之间的关系如图所示.
(1)求出当0≤t≤0.2和t>0.2时,s与t之间的函数解析式.
(2)经过多少小时,乙超过甲
15.甲、乙两个书店举行了购书优惠活动.甲书店:所有图书按标价7折出售;乙书店:所购图书标价总额不超过80元的按原价计费,超过80元的部分打5折.设要购买图书的标价总额为x元,实际支付金额为y元.
(1)根据题意,填写下表:
在乙书店购买图书标价总额/元 60 80 90 100
在乙书店购买图书实际支付金额/元 60 85
(2)请直接写出在甲、乙书店购书金额y1,y2与x的函数解析式.
(3)若只在一家书店购书,请通过计算说明在哪家书店购买更实惠.
16.如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象交x轴于点A(8,0),交y轴于点B.直线y=x-与y轴交于点D,与直线AB交于点C(6,a).M是线段BC上的一个动点(点M不与点C重合),过点M作x轴的垂线交直线CD于点N.设点M的横坐标为m.
(1)求a的值和直线AB的函数解析式.
(2)以线段MN,MC为邻边作 MNQC,直线QC与x轴交于点E.
①当0≤m<时,设线段EQ的长度为l,求l与m之间的关系式;
②连接OQ,AQ,当△AOQ的面积为3时,请直接写出m的值.
17.某动力科学研究院实验基地内装有一段笔直的轨道AB,长度为1 m的金属滑块在上面做往返滑动.如图,滑块首先沿AB方向从左向右匀速滑动,滑动速度为9 m/s,滑动开始前滑块左端与点A重合,当滑块右端到达点B时,滑块停顿2 s,然后再以小于9 m/s的速度匀速返回,直到滑块的左端与点A重合,滑动停止.设时间为t(单位:s)时,滑块左端离点A的距离为l1(单位:m),右端离点B的距离为l2(单位:m),记d=l1-l2,d与t具有函数关系.已知滑块在从左向右的滑动过程中,当t=4.5和5.5时,与之对应的d的两个值互为相反数;滑块从点A出发到最后返回点A,整个过程总用时27 s(含停顿时间).请你根据所给条件解决下列问题:
(1)滑块从点A到点B的滑动过程中,d的值 .(填“由负到正”或“由正到负”)
(2)滑块从点B到点A的滑动过程中,求d与t的函数解析式.
(3)在整个往返过程中,若d=18,求t的值.
参考答案
1.C 2.C 3.C 4.y=3x-3 5.>2.5 <3 6.D
7.一 8. 9.-1 10.120
11.解:(1)由题意知,k==3,即点P(6,2)的“倾斜系数”k的值为3.
(2)①∵点P(a,b)的“倾斜系数”k=2,
∴=2或=2,即a=2b或b=2a,
∴a和b的数量关系为a=2b或b=2a.
②由①知,a=2b或b=2a.
∵a+b=3,∴或
∴OP==.
12.解:(1)由y1=-x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2.
∵y1=-x+1与直线y2=-x交于点B,
∴点B的坐标是(-1,1.5),
∴△AOB的面积=×2×1.5=1.5.
(2)由(1)可知交点B的坐标是(-1,1.5),
由函数图象可知y1>y2时,x>-1.
13.解:(1)∵点A(2,0),AB=,
∴BO===3,
∴点B的坐标为(0,3).
(2)∵△ABC的面积为4,
∴×BC×AO=4,
∴×BC×2=4,即BC=4.
∵BO=3,
∴CO=4-3=1,
∴C(0,-1).
设直线l2的解析式为y=kx+b,则
解得∴直线l2的解析式为y=x-1.
14.解:(1)当0≤t≤0.2时,设s=at,
把(0.2,3)代入s=at,得0.2a=3,解得a=15,
∴s=15t;
当t>0.2时,设s=kt+b,
把(0.2,3)和(0.5,9)代入s=kt+b,
得解得
∴s=20t-1,
∴s与t之间的函数解析式为s=
(2)由(1)可知,当0≤t≤0.2时,乙骑行的速度为15 km/h,而甲的速度为18 km/h,则甲在乙前面,当t>0.2时,乙骑行的速度为20 km/h,甲的速度为18 km/h.
设x小时后,乙超过甲,则18x<20x-1,解得x>0.5.
答:0.5小时后乙超过甲.
15.解:(1)80;90.
(2)根据题意得y1=x,
当0≤x≤80时,y2=x,
当x>80时,y2=80+(x-80)=x+40,
∴y2=
(3)①当0∵x∴在甲书店购买更实惠.
②若x>80,
当x解得x<200,
∴当80当x=x+40时,
解得x=200,
∴当x=200时,在两家书店购买所需费用一样;
当x>x+40时,
解得x>200,
∴当x>200时,在乙书店购买更实惠.
综上所述,当0200时,在乙书店购买更实惠.
16.解:(1)∵点C(6,a)在直线y=x-上,
∴a=×6-=.
∵一次函数y=kx+b的图象过点A(8,0)和点C6,,
∴解得
∴直线AB的函数解析式为y=-x+6.
(2)①∵点M在直线y=-x+6上,且点M的横坐标为m,
∴点M的纵坐标为-m+6.
∵点N在直线y=x-上,且点N的横坐标为m,
∴点N的纵坐标为m-,
∴MN=-m+6-m+=-m.
∵点C(6,),线段EQ的长度为l,
∴CQ=l+.
∵MN=CQ,
∴-m=l+,
即l=6-m.
②或.
提示:∵△AOQ的面积为3,
∴OA·EQ=3,
即×8×EQ=3,
解得EQ=.
∵EQ=6-m,
∴6-m=,∴6-m=或6-m=-,
解得m=或m=,
即m的值为或.
17.解:(1)∵d=l1-l2,
当滑块在点A时,l1=0,d=-l2<0,
当滑块在点B时,l2=0,d=l1>0,
∴d的值由负到正.
故答案为由负到正.
(2)设轨道AB的长为n,当滑块从左向右滑动时,
∵l1+l2+1=n,
∴l2=n-l1-1,
∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1,
∴d是关于t的一次函数.
∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,
∴18×4.5-n+1+(18×5.5-n+1)=0,
解得n=91,
∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).
∵整个过程总用时27 s(含停顿时间).当滑块右端到达点B时,滑块停顿2 s,
∴滑块从点B返回到点A所用的时间为27-10-2=15 s,
∴滑块返回的速度为(91-1)÷15=6(m/s),
∴当12≤t≤27时,l2=6(t-12),
∴l1=91-1-l2=90-6(t-12)=162-6t,
∴l1-l2=162-6t-6(t-12)=-12t+234,
∴d与t的函数解析式为d=-12t+234.
(3)由(2)可知,有两种情况:
①当0≤t≤10时,18t-90=18,
∴t=6;
②当12≤t≤27时,-12t+234=18,
∴t=18.
综上所述,当t=6或18时,d=18.
2
【基础作业】
1.有下列函数:①y=2x;②y=;③y=2x+1;④y=2x2+1.其中y是关于x的一次函数有 ( )
A.1个 B.2个
C.3个 D.4个
2.在函数y=中,自变量x的取值范围是 ( )
A.x≥1 B.x>2
C.x≥1且x≠2 D.x≠2
3.如图,这是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是 ( )
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度
4.将直线y=3x向下平移3个单位长度后所得直线的解析式是 .
5.如图,已知一次函数y=kx+b,观察图象回答下列问题:当x 时,kx+b>0;当x 时,kx+b<1.
【巩固作业】
6.甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(单位:km)与行驶时间t(单位:h)的函数图象如图所示,下列说法正确的有 ( )
①甲车的速度为50 km/h;②乙车用了3 h到达B城;③甲车出发4 h时,乙车追上甲车.
A.0个 B.1个 C.2个 D.3个
7.若点M(k-1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k-1)x+k的图象不经过第 象限.
8.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(单位:km)与甲车行驶时间t(单位:h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.
9.已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所有可能取得的整数值为 .
10.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 秒.
11.在平面直角坐标系中,P(a,b)是第一象限内一点,给出如下定义:k1=和k2=两个值中的最大值叫做点P的“倾斜系数”k.
(1)求点P(6,2)的“倾斜系数”k的值.
(2)①若点P(a,b)的“倾斜系数”k=2,请写出a和b的数量关系,并说明理由;
②若点P(a,b)的“倾斜系数”k=2,且a+b=3,求OP的长.
12.如图,已知直线y1=-x+1与x轴交于点A,与直线y2=-x交于点B.
(1)求△AOB的面积.
(2)求y1>y2时x的取值范围.
13.如图,过点A(2,0)的两条直线l1,l2分别交y轴于B,C两点,其中点B在原点O上方,点C在原点下方,已知AB=.
(1)求点B的坐标.
(2)若△ABC的面积为4,求直线l2的解析式.
【素养作业】
14.随着“公园城市”建设的不断推进,我市绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是18 km/h,乙骑行的路程s(km)与骑行的时间t(h)之间的关系如图所示.
(1)求出当0≤t≤0.2和t>0.2时,s与t之间的函数解析式.
(2)经过多少小时,乙超过甲
15.甲、乙两个书店举行了购书优惠活动.甲书店:所有图书按标价7折出售;乙书店:所购图书标价总额不超过80元的按原价计费,超过80元的部分打5折.设要购买图书的标价总额为x元,实际支付金额为y元.
(1)根据题意,填写下表:
在乙书店购买图书标价总额/元 60 80 90 100
在乙书店购买图书实际支付金额/元 60 85
(2)请直接写出在甲、乙书店购书金额y1,y2与x的函数解析式.
(3)若只在一家书店购书,请通过计算说明在哪家书店购买更实惠.
16.如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象交x轴于点A(8,0),交y轴于点B.直线y=x-与y轴交于点D,与直线AB交于点C(6,a).M是线段BC上的一个动点(点M不与点C重合),过点M作x轴的垂线交直线CD于点N.设点M的横坐标为m.
(1)求a的值和直线AB的函数解析式.
(2)以线段MN,MC为邻边作 MNQC,直线QC与x轴交于点E.
①当0≤m<时,设线段EQ的长度为l,求l与m之间的关系式;
②连接OQ,AQ,当△AOQ的面积为3时,请直接写出m的值.
17.某动力科学研究院实验基地内装有一段笔直的轨道AB,长度为1 m的金属滑块在上面做往返滑动.如图,滑块首先沿AB方向从左向右匀速滑动,滑动速度为9 m/s,滑动开始前滑块左端与点A重合,当滑块右端到达点B时,滑块停顿2 s,然后再以小于9 m/s的速度匀速返回,直到滑块的左端与点A重合,滑动停止.设时间为t(单位:s)时,滑块左端离点A的距离为l1(单位:m),右端离点B的距离为l2(单位:m),记d=l1-l2,d与t具有函数关系.已知滑块在从左向右的滑动过程中,当t=4.5和5.5时,与之对应的d的两个值互为相反数;滑块从点A出发到最后返回点A,整个过程总用时27 s(含停顿时间).请你根据所给条件解决下列问题:
(1)滑块从点A到点B的滑动过程中,d的值 .(填“由负到正”或“由正到负”)
(2)滑块从点B到点A的滑动过程中,求d与t的函数解析式.
(3)在整个往返过程中,若d=18,求t的值.
参考答案
1.C 2.C 3.C 4.y=3x-3 5.>2.5 <3 6.D
7.一 8. 9.-1 10.120
11.解:(1)由题意知,k==3,即点P(6,2)的“倾斜系数”k的值为3.
(2)①∵点P(a,b)的“倾斜系数”k=2,
∴=2或=2,即a=2b或b=2a,
∴a和b的数量关系为a=2b或b=2a.
②由①知,a=2b或b=2a.
∵a+b=3,∴或
∴OP==.
12.解:(1)由y1=-x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2.
∵y1=-x+1与直线y2=-x交于点B,
∴点B的坐标是(-1,1.5),
∴△AOB的面积=×2×1.5=1.5.
(2)由(1)可知交点B的坐标是(-1,1.5),
由函数图象可知y1>y2时,x>-1.
13.解:(1)∵点A(2,0),AB=,
∴BO===3,
∴点B的坐标为(0,3).
(2)∵△ABC的面积为4,
∴×BC×AO=4,
∴×BC×2=4,即BC=4.
∵BO=3,
∴CO=4-3=1,
∴C(0,-1).
设直线l2的解析式为y=kx+b,则
解得∴直线l2的解析式为y=x-1.
14.解:(1)当0≤t≤0.2时,设s=at,
把(0.2,3)代入s=at,得0.2a=3,解得a=15,
∴s=15t;
当t>0.2时,设s=kt+b,
把(0.2,3)和(0.5,9)代入s=kt+b,
得解得
∴s=20t-1,
∴s与t之间的函数解析式为s=
(2)由(1)可知,当0≤t≤0.2时,乙骑行的速度为15 km/h,而甲的速度为18 km/h,则甲在乙前面,当t>0.2时,乙骑行的速度为20 km/h,甲的速度为18 km/h.
设x小时后,乙超过甲,则18x<20x-1,解得x>0.5.
答:0.5小时后乙超过甲.
15.解:(1)80;90.
(2)根据题意得y1=x,
当0≤x≤80时,y2=x,
当x>80时,y2=80+(x-80)=x+40,
∴y2=
(3)①当0
②若x>80,
当x
∴当80
解得x=200,
∴当x=200时,在两家书店购买所需费用一样;
当x>x+40时,
解得x>200,
∴当x>200时,在乙书店购买更实惠.
综上所述,当0
16.解:(1)∵点C(6,a)在直线y=x-上,
∴a=×6-=.
∵一次函数y=kx+b的图象过点A(8,0)和点C6,,
∴解得
∴直线AB的函数解析式为y=-x+6.
(2)①∵点M在直线y=-x+6上,且点M的横坐标为m,
∴点M的纵坐标为-m+6.
∵点N在直线y=x-上,且点N的横坐标为m,
∴点N的纵坐标为m-,
∴MN=-m+6-m+=-m.
∵点C(6,),线段EQ的长度为l,
∴CQ=l+.
∵MN=CQ,
∴-m=l+,
即l=6-m.
②或.
提示:∵△AOQ的面积为3,
∴OA·EQ=3,
即×8×EQ=3,
解得EQ=.
∵EQ=6-m,
∴6-m=,∴6-m=或6-m=-,
解得m=或m=,
即m的值为或.
17.解:(1)∵d=l1-l2,
当滑块在点A时,l1=0,d=-l2<0,
当滑块在点B时,l2=0,d=l1>0,
∴d的值由负到正.
故答案为由负到正.
(2)设轨道AB的长为n,当滑块从左向右滑动时,
∵l1+l2+1=n,
∴l2=n-l1-1,
∴d=l1-l2=l1-(n-l1-1)=2l1-n+1=2×9t-n+1=18t-n+1,
∴d是关于t的一次函数.
∵当t=4.5和5.5时,与之对应的d的两个值互为相反数,
∴18×4.5-n+1+(18×5.5-n+1)=0,
解得n=91,
∴滑块从点A到点B所用的时间为(91-1)÷9=10(s).
∵整个过程总用时27 s(含停顿时间).当滑块右端到达点B时,滑块停顿2 s,
∴滑块从点B返回到点A所用的时间为27-10-2=15 s,
∴滑块返回的速度为(91-1)÷15=6(m/s),
∴当12≤t≤27时,l2=6(t-12),
∴l1=91-1-l2=90-6(t-12)=162-6t,
∴l1-l2=162-6t-6(t-12)=-12t+234,
∴d与t的函数解析式为d=-12t+234.
(3)由(2)可知,有两种情况:
①当0≤t≤10时,18t-90=18,
∴t=6;
②当12≤t≤27时,-12t+234=18,
∴t=18.
综上所述,当t=6或18时,d=18.
2
