人教版七年级数学下册第五章 相交线与平行线章节练习题 (1)(含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线章节练习题 (1)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 08:48:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级数学下册第五章 相交线与平行线章节练习题
一、单选题(共10小题,每小题3分,满分30分)
1.如图,下列各组角中,互为对顶角的是( )
A.和 B.和 C.和 D.和
2.如图所示的图形中,线段的长表示点到直线的距离的是( )
A. B. C. D.
3.过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点处
C.这条线段的延长线上 D.以上都有可能
4.如图,与是同旁内角的是( )
A. B. C. D.
5.下列生活实例中:①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有( )
A.个 B.个 C.个 D.个
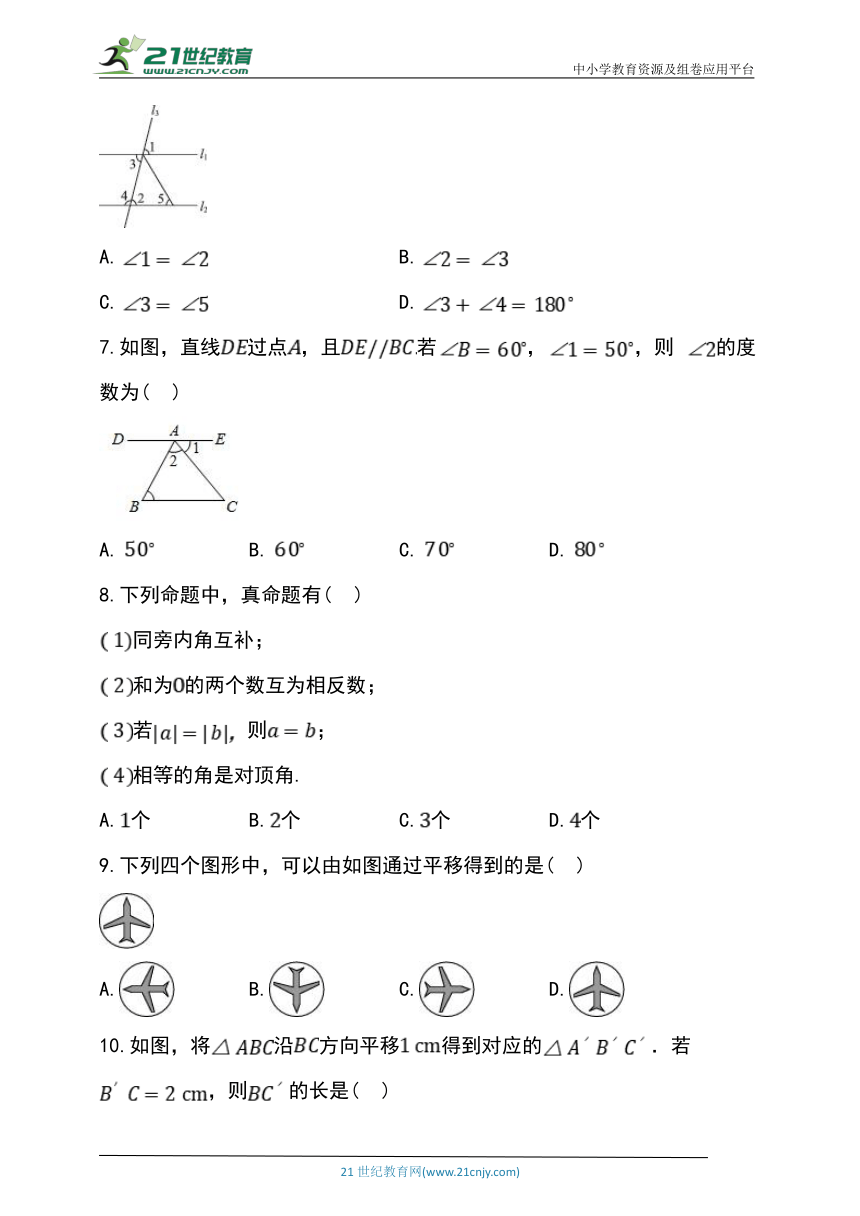
6.如图,下列选项中,不可以得到的是( )
A. B.
C. D.
7.如图,直线过点,且若,,则 的度数为( )
A. B. C. D.
8.下列命题中,真命题有( )
同旁内角互补;
和为的两个数互为相反数;
若则;
相等的角是对顶角.
A.个 B.个 C.个 D.个
9.下列四个图形中,可以由如图通过平移得到的是( )
A. B. C. D.
10.如图,将沿方向平移得到对应的.若,则的长是( )
A. B. C. D.
二、填空题(共11小题,每小题3分,满分33分)
11.如图是一把剪刀,若则( ).
12.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是,理由是( ).
13.如图,点是直线上一点,,是的角平分线,是的角平分线,则的度数是( ).
14.如图,点是延长线上一点,如果添加一个条件,使,则可添加的条件为( ).(任意添加一个符合题意的条件即可)
15.将一副三角尺如图所示放置,其中,则( )度.
16.某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线,等反射后都沿着与平行的方向射出.若,,则( ).
17.已知直线∥b,把一块含角的直角三角板按如图方式放置,若,则 .
18.如图,则( ).
19.命题“两直线平行,内错角相等”的题设是( ),结论是( ).
20.如图,,平分,则 .
21.如图,三角形的边的长为,将三角形平移得到三角形,且,则阴影部分的面积为( ).
三、解答题(共6小题,满分37分)
22.如图,将三角形平行移动后得到三角形′′′,其中点平行移动到了点′.画出′′′. (4分)
23.如图,一个由条线段构成的“鱼”形图案,其中,,,找出图中的平行线,并说明理由. (6分)
24. 如图,,,直线与,的延长线分别交于点,,求证:(6分)
25.如图,在直角三角形中,,,,将沿方向向右平移得到,若,. (7分)
(1)求向右平移的距离的长;
(2)求四边形的周长.
26.填空完成推理过程:如图,已知于点,于点,.试判断与的位置关系,并说明你的理由.(7分)
解: .
理由:∵ ),
∴ = ).
∵ ),
∴,即,
∴ ( ).
27.如图,已知,,,求的度数.(7分)
参考答案
1.A
2.A
3.D
4.D
5.D
6.C
7.C
8.A
9.D
10.C
11.
12.垂线段最短
13.
14.或或或(答案不唯一)
15.
16.
17.
18.
19.两条平行线被第三条直线所截;内错角相等
20.
21.
22.图中的三角形′′′即为所求.
23.解:,.
理由如下:
∵,,
∴,
∴.
∵,,
∴,
∴.
24.证明:,
,
,
,
,
.
25.(1)∵沿方向向右平移得到,
∴,.
∵,,
∴
(2)四边形的周长
26.解:.
理由:∵(已知),
∴(垂直的定义).
∵(已知),
∴,即,
∴(内错角相等,两直线平行).
27.如图所示,过点作,
∵,
∴,
∴.
∵,
∴.
∵,
∴,
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级数学下册第五章 相交线与平行线章节练习题
一、单选题(共10小题,每小题3分,满分30分)
1.如图,下列各组角中,互为对顶角的是( )
A.和 B.和 C.和 D.和
2.如图所示的图形中,线段的长表示点到直线的距离的是( )
A. B. C. D.
3.过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点处
C.这条线段的延长线上 D.以上都有可能
4.如图,与是同旁内角的是( )
A. B. C. D.
5.下列生活实例中:①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有( )
A.个 B.个 C.个 D.个
6.如图,下列选项中,不可以得到的是( )
A. B.
C. D.
7.如图,直线过点,且若,,则 的度数为( )
A. B. C. D.
8.下列命题中,真命题有( )
同旁内角互补;
和为的两个数互为相反数;
若则;
相等的角是对顶角.
A.个 B.个 C.个 D.个
9.下列四个图形中,可以由如图通过平移得到的是( )
A. B. C. D.
10.如图,将沿方向平移得到对应的.若,则的长是( )
A. B. C. D.
二、填空题(共11小题,每小题3分,满分33分)
11.如图是一把剪刀,若则( ).
12.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是,理由是( ).
13.如图,点是直线上一点,,是的角平分线,是的角平分线,则的度数是( ).
14.如图,点是延长线上一点,如果添加一个条件,使,则可添加的条件为( ).(任意添加一个符合题意的条件即可)
15.将一副三角尺如图所示放置,其中,则( )度.
16.某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线,等反射后都沿着与平行的方向射出.若,,则( ).
17.已知直线∥b,把一块含角的直角三角板按如图方式放置,若,则 .
18.如图,则( ).
19.命题“两直线平行,内错角相等”的题设是( ),结论是( ).
20.如图,,平分,则 .
21.如图,三角形的边的长为,将三角形平移得到三角形,且,则阴影部分的面积为( ).
三、解答题(共6小题,满分37分)
22.如图,将三角形平行移动后得到三角形′′′,其中点平行移动到了点′.画出′′′. (4分)
23.如图,一个由条线段构成的“鱼”形图案,其中,,,找出图中的平行线,并说明理由. (6分)
24. 如图,,,直线与,的延长线分别交于点,,求证:(6分)
25.如图,在直角三角形中,,,,将沿方向向右平移得到,若,. (7分)
(1)求向右平移的距离的长;
(2)求四边形的周长.
26.填空完成推理过程:如图,已知于点,于点,.试判断与的位置关系,并说明你的理由.(7分)
解: .
理由:∵ ),
∴ = ).
∵ ),
∴,即,
∴ ( ).
27.如图,已知,,,求的度数.(7分)
参考答案
1.A
2.A
3.D
4.D
5.D
6.C
7.C
8.A
9.D
10.C
11.
12.垂线段最短
13.
14.或或或(答案不唯一)
15.
16.
17.
18.
19.两条平行线被第三条直线所截;内错角相等
20.
21.
22.图中的三角形′′′即为所求.
23.解:,.
理由如下:
∵,,
∴,
∴.
∵,,
∴,
∴.
24.证明:,
,
,
,
,
.
25.(1)∵沿方向向右平移得到,
∴,.
∵,,
∴
(2)四边形的周长
26.解:.
理由:∵(已知),
∴(垂直的定义).
∵(已知),
∴,即,
∴(内错角相等,两直线平行).
27.如图所示,过点作,
∵,
∴,
∴.
∵,
∴.
∵,
∴,
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
