7.2探索平行线的性质 苏科版初中数学七年级下册同步练习(含解析)
文档属性
| 名称 | 7.2探索平行线的性质 苏科版初中数学七年级下册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 615.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 11:13:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.2探索平行线的性质苏科版初中数学七年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,一艘快艇向正东方向行驶至点时,接到指令向右转,航行到处,再向左转,航行到处,再向右转继续航行,此时这艘快艇的航行方向为( )
A. 北偏西 B. 北偏西 C. 南偏东 D. 南偏东
2.如图,为一长条形纸带,,将沿折叠,、两点分别与、对应,若,则的度数是( )
A. B. C. D.
3.如图,在平行线,之间放置一块直角三角尺,三角尺的锐角顶点,分别在直线,上.若,则的度数是
( )
A. B. C. D.
4.如图,,与的角平分线交于点,且,已知,若,,则下列等式中成立的是
( )
A. B. C. D.
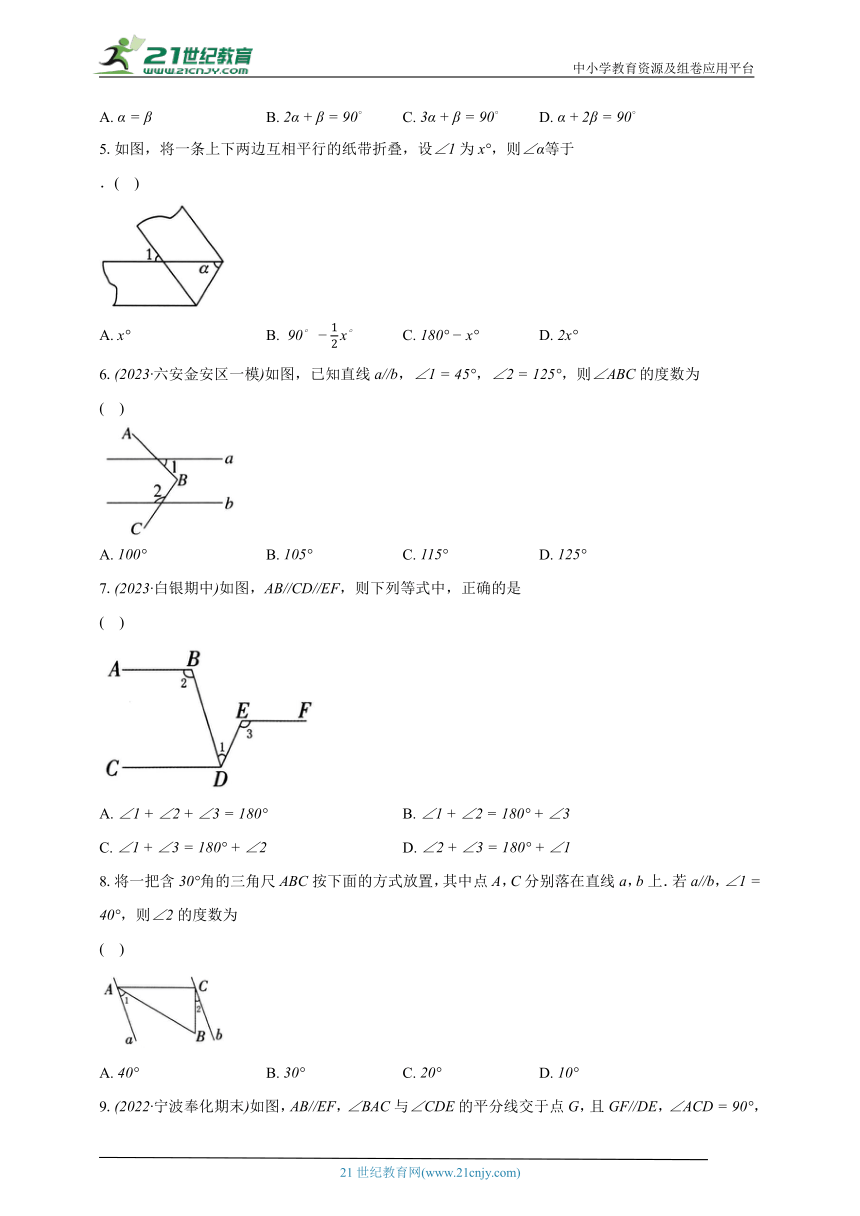
5.如图,将一条上下两边互相平行的纸带折叠,设为,则等于
.( )
A. B. C. D.
6.六安金安区一模如图,已知直线,,,则的度数为
( )
A. B. C. D.
7.白银期中如图,,则下列等式中,正确的是
( )
A. B.
C. D.
8.将一把含角的三角尺按下面的方式放置,其中点,分别落在直线,上.若,,则的度数为
( )
A. B. C. D.
9.宁波奉化期末如图,,与的平分线交于点,且,,连接若,,则下列等式中,成立的是
( )
A. B. C. D.
10.如图,把一张长方形纸片沿折叠后,、分别在、的位置上,与的交点为,若,则( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,直线,直线交于点,交于点,过点的直线交于点若,,则
12.如图,平分,,若,,则
13.七彩云南少数民族传统艺术表演,是七彩云南欢乐世界的王牌演艺节目,它荟萃云南人文之美,深受观众喜爱.在展演中,舞台上的灯光由灯带上位于点和点的两盏激光灯控制.如图,光线与灯带的夹角,当时,光线与灯带的夹角 .
14.
如下图,将一个含角的直角三角尺按如图所示的位置摆放在直尺上.若,则的度数为
将一副直角三角尺按如下图所示的方式摆放,点在的延长线上,且,则的度数为
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在三角形中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
判断与的位置关系,并说明理由;
若,且,求的度数.
16.本小题分
如图,的延长线与的延长线交于点,,,.
求的度数;
试说明:.
17.本小题分
如图,点在的一边上,过点的直线,平分,.
若,求的度数;
当为多少度时,分成的两部分,并说明理由.
18.本小题分
如图,点在线段上,点、在线段上,,.
试说明:;
若于点,平分,,求的度数.
19.本小题分
如图,,,探索与的数量关系,并说明理由.
20.本小题分
如图,平分,,,、交于点.
说明:;
若,求________的度数.请从“,”中选择一项填在空格处填写序号,并写出求解过程.
答案和解析
1.【答案】
【解析】如图,由题意得,,因为,所以.
因为,所以因为,所以.
又因为,所以,所以此时的航行方向为南偏东,故选C.
2.【答案】
【解析】由翻折的性质可知因为,
设,则,,所以,解得,
所以.
因为,所以,所以,故选C.
3.【答案】
【解析】设三角尺的直角顶点为,过点作直线交于点,则因为,所以,所以因为,所以,即又因为,所以.
4.【答案】
【解析】解:如图,过作,连接并延长,
,
,
,
又是的外角,是的外角,
,
,
与的角平分线交于点,
,,
,
又,,
,
,
即,
,
,
故选:
过作,连接并延长,依据平行线的性质以及三角形的外角性质,即可得到,,进而得出
本题主要考查了平行线的性质,熟练掌握“两直线平行,同旁内角互补”是解题的关键.
5.【答案】
【解析】【分析】
本题考查了平行线的性质和折叠的性质,根据平行线的性质和对顶角得到,,再根据折叠的性质可得,即可求解.
【解答】
解:延长纸带下边,如图,由题意,可知,, 由折叠性质,得,所以, 所以,即, 所以 .
6.【答案】
【解析】【分析】
本题考查平行线的性质,解答本题的关键是明确题意,利用平行线的性质解答.根据平行线的性质和,,可以得到的度数,本题得以解决.
【解答】
解:作,
因为,
所以,
所以,
所以,,
因为,,
所以,,
所以.
故选A.
7.【答案】
【解析】【分析】
本题主要考查平行线的性质,从复杂图形中找出内错角,同旁内角是解题的关键.
根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等可得,而,整理可得.
【解答】
解:,
,,
又,
即,
.
故选:.
8.【答案】
【解析】解:如图,过点作,
,
,
,
,
,
,
在三角尺中,易知,,
.
.
故选:.
过点作,可得,,可得,可得,根据角的和差可求的度数.
本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.
9.【答案】
【解析】如图,过点作 ,连接并延长至点.
,
.
过点作 ,
.
,
.
.
,
易得.
,,
.
同理,可得.
.
.
与的平分线交于点,
,.
.
,即.
又 , ,
,.
.
,
即.
.
故选:.
过作,连接并延长,依据平行线的性质,即可得到,,进而得出.
本题主要考查了平行线的性质,熟练掌握“两直线平行,同旁内角互补”是解题的关键.
10.【答案】
【解析】解:长方形对边,
,
,
由翻折的性质得:,
,
故选:.
根据两直线平行,同旁内角互补可得,再根据翻折的性质和平角的定义列式计算,即可求出.
本题主要考查平行线的性质,折叠的性质,熟练掌握平行线的性质和折叠的性质是解题的关键.
11.【答案】
【解析】如图,因为,所以.
因为,所以.
因为,,所以.
因为,所以.
12.【答案】
【解析】因为,所以.
因为,所以,所以,所以.
因为,所以,所以因为平分,
所以因为,所以,所以.
又,所以.
13.【答案】或
【解析】如图,分情况讨论:
当在的右侧时,因为,,所以;
当在的左侧时,.
14.【答案】【小题】
【小题】
【解析】 略
略
15.【答案】【小题】
理由如下:
,,.
,,
.
【小题】
由,得,
,.
,.
,,,
.
,,
解得,.
【解析】 见答案
见答案
16.【答案】【小题】
,,.
,
.
【小题】
,,,,
即,.
【解析】 见答案
见答案
17.【答案】【小题】
,
两直线平行,同位角相等.
,.
平角定义,
.
平分,
角平分线的定义,
.
【小题】
当或时,分成两部分.理由如下:
当时,,
,.
又平分,,
,
即分成两部分;
当时,,
,.
又平分,,
,
即分成两部分.
【解析】 见答案
见答案
18.【答案】【小题】
,.
,,.
【小题】
,.
,,
.
平分,,
,
的度数为.
【解析】 见答案
见答案
19.【答案】理由如下:
,,,
,.
,,
,.
【解析】见答案
20.【答案】【小题】
因为平分,,所以.
因为,所以,所以.
【小题】
填因为平分,,所以.
因为,所以,所以.
填因为,所以又,
所以,所以.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.2探索平行线的性质苏科版初中数学七年级下册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,一艘快艇向正东方向行驶至点时,接到指令向右转,航行到处,再向左转,航行到处,再向右转继续航行,此时这艘快艇的航行方向为( )
A. 北偏西 B. 北偏西 C. 南偏东 D. 南偏东
2.如图,为一长条形纸带,,将沿折叠,、两点分别与、对应,若,则的度数是( )
A. B. C. D.
3.如图,在平行线,之间放置一块直角三角尺,三角尺的锐角顶点,分别在直线,上.若,则的度数是
( )
A. B. C. D.
4.如图,,与的角平分线交于点,且,已知,若,,则下列等式中成立的是
( )
A. B. C. D.
5.如图,将一条上下两边互相平行的纸带折叠,设为,则等于
.( )
A. B. C. D.
6.六安金安区一模如图,已知直线,,,则的度数为
( )
A. B. C. D.
7.白银期中如图,,则下列等式中,正确的是
( )
A. B.
C. D.
8.将一把含角的三角尺按下面的方式放置,其中点,分别落在直线,上.若,,则的度数为
( )
A. B. C. D.
9.宁波奉化期末如图,,与的平分线交于点,且,,连接若,,则下列等式中,成立的是
( )
A. B. C. D.
10.如图,把一张长方形纸片沿折叠后,、分别在、的位置上,与的交点为,若,则( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,直线,直线交于点,交于点,过点的直线交于点若,,则
12.如图,平分,,若,,则
13.七彩云南少数民族传统艺术表演,是七彩云南欢乐世界的王牌演艺节目,它荟萃云南人文之美,深受观众喜爱.在展演中,舞台上的灯光由灯带上位于点和点的两盏激光灯控制.如图,光线与灯带的夹角,当时,光线与灯带的夹角 .
14.
如下图,将一个含角的直角三角尺按如图所示的位置摆放在直尺上.若,则的度数为
将一副直角三角尺按如下图所示的方式摆放,点在的延长线上,且,则的度数为
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在三角形中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
判断与的位置关系,并说明理由;
若,且,求的度数.
16.本小题分
如图,的延长线与的延长线交于点,,,.
求的度数;
试说明:.
17.本小题分
如图,点在的一边上,过点的直线,平分,.
若,求的度数;
当为多少度时,分成的两部分,并说明理由.
18.本小题分
如图,点在线段上,点、在线段上,,.
试说明:;
若于点,平分,,求的度数.
19.本小题分
如图,,,探索与的数量关系,并说明理由.
20.本小题分
如图,平分,,,、交于点.
说明:;
若,求________的度数.请从“,”中选择一项填在空格处填写序号,并写出求解过程.
答案和解析
1.【答案】
【解析】如图,由题意得,,因为,所以.
因为,所以因为,所以.
又因为,所以,所以此时的航行方向为南偏东,故选C.
2.【答案】
【解析】由翻折的性质可知因为,
设,则,,所以,解得,
所以.
因为,所以,所以,故选C.
3.【答案】
【解析】设三角尺的直角顶点为,过点作直线交于点,则因为,所以,所以因为,所以,即又因为,所以.
4.【答案】
【解析】解:如图,过作,连接并延长,
,
,
,
又是的外角,是的外角,
,
,
与的角平分线交于点,
,,
,
又,,
,
,
即,
,
,
故选:
过作,连接并延长,依据平行线的性质以及三角形的外角性质,即可得到,,进而得出
本题主要考查了平行线的性质,熟练掌握“两直线平行,同旁内角互补”是解题的关键.
5.【答案】
【解析】【分析】
本题考查了平行线的性质和折叠的性质,根据平行线的性质和对顶角得到,,再根据折叠的性质可得,即可求解.
【解答】
解:延长纸带下边,如图,由题意,可知,, 由折叠性质,得,所以, 所以,即, 所以 .
6.【答案】
【解析】【分析】
本题考查平行线的性质,解答本题的关键是明确题意,利用平行线的性质解答.根据平行线的性质和,,可以得到的度数,本题得以解决.
【解答】
解:作,
因为,
所以,
所以,
所以,,
因为,,
所以,,
所以.
故选A.
7.【答案】
【解析】【分析】
本题主要考查平行线的性质,从复杂图形中找出内错角,同旁内角是解题的关键.
根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等可得,而,整理可得.
【解答】
解:,
,,
又,
即,
.
故选:.
8.【答案】
【解析】解:如图,过点作,
,
,
,
,
,
,
在三角尺中,易知,,
.
.
故选:.
过点作,可得,,可得,可得,根据角的和差可求的度数.
本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.
9.【答案】
【解析】如图,过点作 ,连接并延长至点.
,
.
过点作 ,
.
,
.
.
,
易得.
,,
.
同理,可得.
.
.
与的平分线交于点,
,.
.
,即.
又 , ,
,.
.
,
即.
.
故选:.
过作,连接并延长,依据平行线的性质,即可得到,,进而得出.
本题主要考查了平行线的性质,熟练掌握“两直线平行,同旁内角互补”是解题的关键.
10.【答案】
【解析】解:长方形对边,
,
,
由翻折的性质得:,
,
故选:.
根据两直线平行,同旁内角互补可得,再根据翻折的性质和平角的定义列式计算,即可求出.
本题主要考查平行线的性质,折叠的性质,熟练掌握平行线的性质和折叠的性质是解题的关键.
11.【答案】
【解析】如图,因为,所以.
因为,所以.
因为,,所以.
因为,所以.
12.【答案】
【解析】因为,所以.
因为,所以,所以,所以.
因为,所以,所以因为平分,
所以因为,所以,所以.
又,所以.
13.【答案】或
【解析】如图,分情况讨论:
当在的右侧时,因为,,所以;
当在的左侧时,.
14.【答案】【小题】
【小题】
【解析】 略
略
15.【答案】【小题】
理由如下:
,,.
,,
.
【小题】
由,得,
,.
,.
,,,
.
,,
解得,.
【解析】 见答案
见答案
16.【答案】【小题】
,,.
,
.
【小题】
,,,,
即,.
【解析】 见答案
见答案
17.【答案】【小题】
,
两直线平行,同位角相等.
,.
平角定义,
.
平分,
角平分线的定义,
.
【小题】
当或时,分成两部分.理由如下:
当时,,
,.
又平分,,
,
即分成两部分;
当时,,
,.
又平分,,
,
即分成两部分.
【解析】 见答案
见答案
18.【答案】【小题】
,.
,,.
【小题】
,.
,,
.
平分,,
,
的度数为.
【解析】 见答案
见答案
19.【答案】理由如下:
,,,
,.
,,
,.
【解析】见答案
20.【答案】【小题】
因为平分,,所以.
因为,所以,所以.
【小题】
填因为平分,,所以.
因为,所以,所以.
填因为,所以又,
所以,所以.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
