新课标A版必修5解三角形《余弦定理》第一课时
文档属性
| 名称 | 新课标A版必修5解三角形《余弦定理》第一课时 |  | |
| 格式 | rar | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-10 22:06:00 | ||
图片预览



文档简介
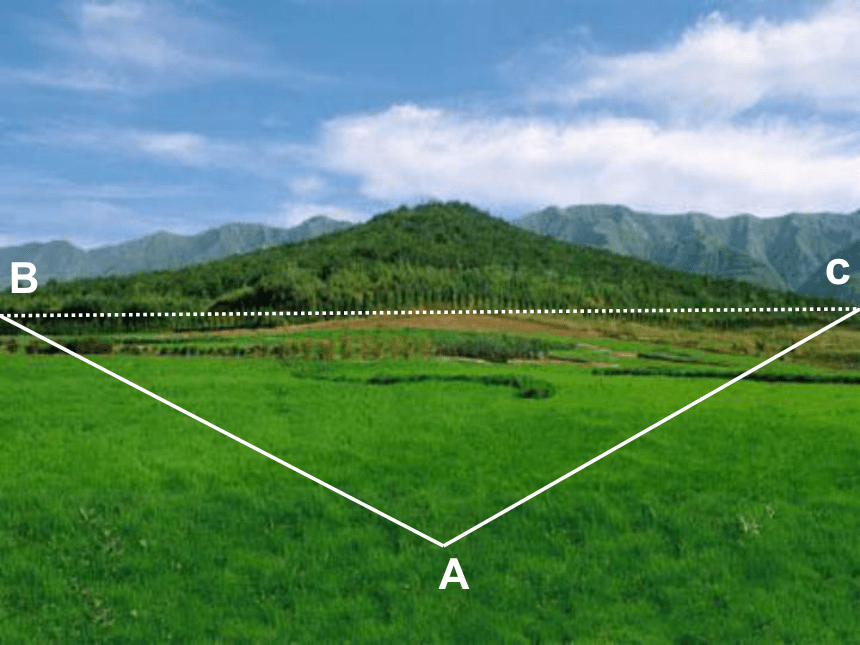
课件18张PPT。1.1.2余弦定理复习回顾正弦定理:可以解决两类有关三角形的问题:(1)已知两角和任一边。(2)已知两边和其中一边的对角。变形:解惟一解的情况有两解、一解、无解。ABc抽象为一个数学问题:
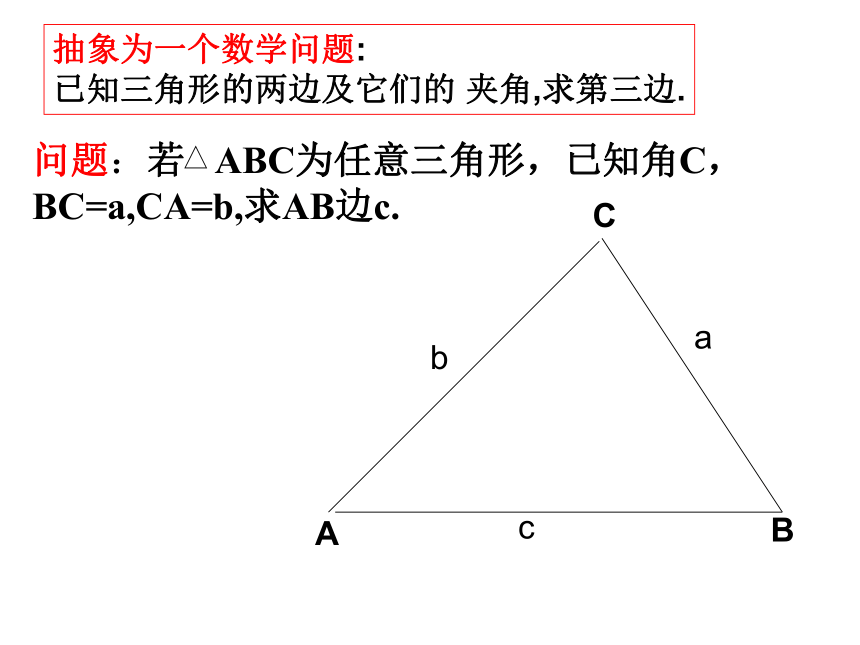
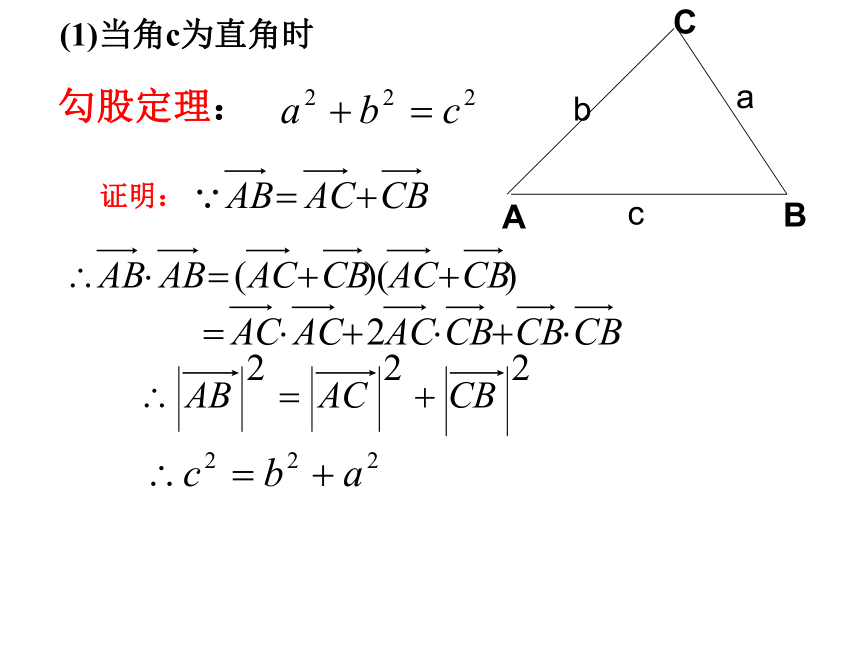
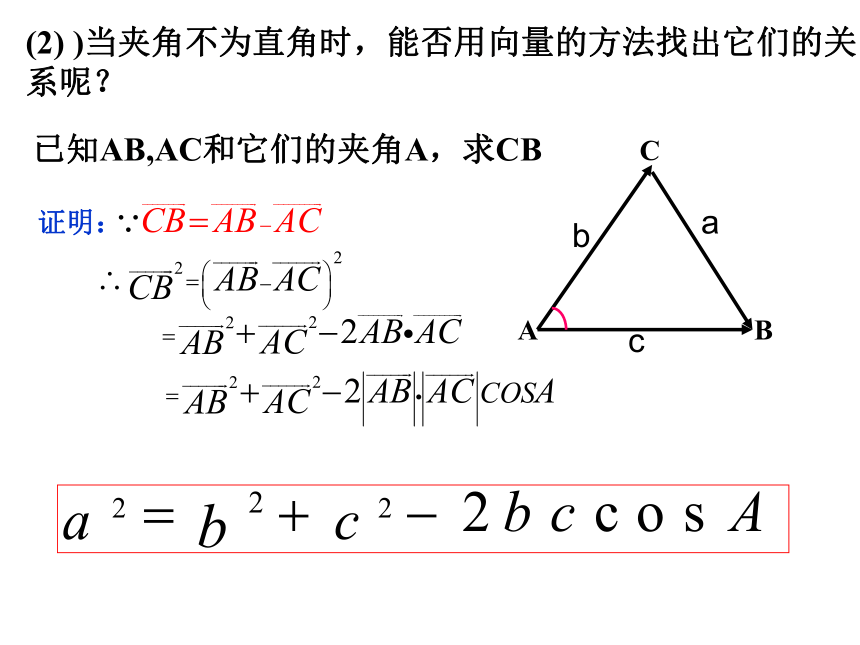
已知三角形的两边及它们的 夹角,求第三边.ABC问题:若 ABC为任意三角形,已知角C,BC=a,CA=b,求AB边c.勾股定理:证明:(1)当角c为直角时 证明:(2) )当夹角不为直角时,能否用向量的方法找出它们的关系呢?已知AB,AC和它们的夹角A,求CB余弦定理: 三角形任一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.由余弦定理变形得:应用:已知三条边求角度.应用:已知两边和一个夹角,
求第三边.解惟一解惟一与勾股定理有何联系?当 时当 时当 时C为钝角;C为锐角.C为直角.例3:在⊿ABC中,已知b=60cm,c=34cm,A=41°,解三角形(角度精确到1°,边长精确到1cm).解:根据余弦定理,a2=b2+c2-2bccosA
=602+342-2×60×34× cos41°≈1676.82
所以 a≈41(cm)由正弦定理得,因为c不是三角形中最大的边,所以C是锐角,利用计算器得
C≈33°
B=180°-(A+C)=180°-(41°+33°)=106°求角C有其他解法吗?例4,在⊿ABC中,已知a=134.6cm,b=87.8cm,c=161.7cm,解三角形(角度精确到1′)。解:由余弦定理的推论得:A≈56°20′;B≈32°53′C= 180°-(A+B)≈ 180°-( 56°20′+ 32°53′ )
=90°47′练习:解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9 - 2×2×3×
=7
∴BC=1.在△ABC中,已知AB=2,AC=3,A= ,求BC的长2.在ΔABC中,已知a=7,b=10,c=6,求A、B和C解:∵ =0.725=0.8071∴ B=180°-(A+C)≈100°∴ A≈44°∴ C≈36°,变式:已知不变,结论换成判定的形状。3.在△ABC中,若a2=b2+c2,则△ABC为 ;
若a2>b2+c2,则△ABC为_____;
若a2<b2+c2且b2<a2+c2且c2<a2+b2,
则△ABC为:_______ 判断三角形ABC的形状一钝角三角形的边长为连续自然数,则这三边长为( )
分析: 要看哪一组符合要求,只需检验哪一个选项中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足BA、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6思考题:小结:余弦定理应用:1、已知两条边和一个夹角,求第三条边。
2、已知三条边,求三个角。判断三角形的形状。应用正、余弦定理可解四类中三角形边角问题:
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求其他的边和角。
(正弦定理)
(3)已知两边和它们的夹角,求第三边和其他两个角;
(4)已知三边,求三个角。
(余弦定理)
已知三角形的两边及它们的 夹角,求第三边.ABC问题:若 ABC为任意三角形,已知角C,BC=a,CA=b,求AB边c.勾股定理:证明:(1)当角c为直角时 证明:(2) )当夹角不为直角时,能否用向量的方法找出它们的关系呢?已知AB,AC和它们的夹角A,求CB余弦定理: 三角形任一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.由余弦定理变形得:应用:已知三条边求角度.应用:已知两边和一个夹角,
求第三边.解惟一解惟一与勾股定理有何联系?当 时当 时当 时C为钝角;C为锐角.C为直角.例3:在⊿ABC中,已知b=60cm,c=34cm,A=41°,解三角形(角度精确到1°,边长精确到1cm).解:根据余弦定理,a2=b2+c2-2bccosA
=602+342-2×60×34× cos41°≈1676.82
所以 a≈41(cm)由正弦定理得,因为c不是三角形中最大的边,所以C是锐角,利用计算器得
C≈33°
B=180°-(A+C)=180°-(41°+33°)=106°求角C有其他解法吗?例4,在⊿ABC中,已知a=134.6cm,b=87.8cm,c=161.7cm,解三角形(角度精确到1′)。解:由余弦定理的推论得:A≈56°20′;B≈32°53′C= 180°-(A+B)≈ 180°-( 56°20′+ 32°53′ )
=90°47′练习:解:由余弦定理可知
BC2=AB2+AC2-2AB×AC·cosA
=4+9 - 2×2×3×
=7
∴BC=1.在△ABC中,已知AB=2,AC=3,A= ,求BC的长2.在ΔABC中,已知a=7,b=10,c=6,求A、B和C解:∵ =0.725=0.8071∴ B=180°-(A+C)≈100°∴ A≈44°∴ C≈36°,变式:已知不变,结论换成判定的形状。3.在△ABC中,若a2=b2+c2,则△ABC为 ;
若a2>b2+c2,则△ABC为_____;
若a2<b2+c2且b2<a2+c2且c2<a2+b2,
则△ABC为:_______ 判断三角形ABC的形状一钝角三角形的边长为连续自然数,则这三边长为( )
分析: 要看哪一组符合要求,只需检验哪一个选项中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足BA、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6思考题:小结:余弦定理应用:1、已知两条边和一个夹角,求第三条边。
2、已知三条边,求三个角。判断三角形的形状。应用正、余弦定理可解四类中三角形边角问题:
(1)已知两角和任意一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求其他的边和角。
(正弦定理)
(3)已知两边和它们的夹角,求第三边和其他两个角;
(4)已知三边,求三个角。
(余弦定理)
