《等比数列》第一课时
图片预览





文档简介
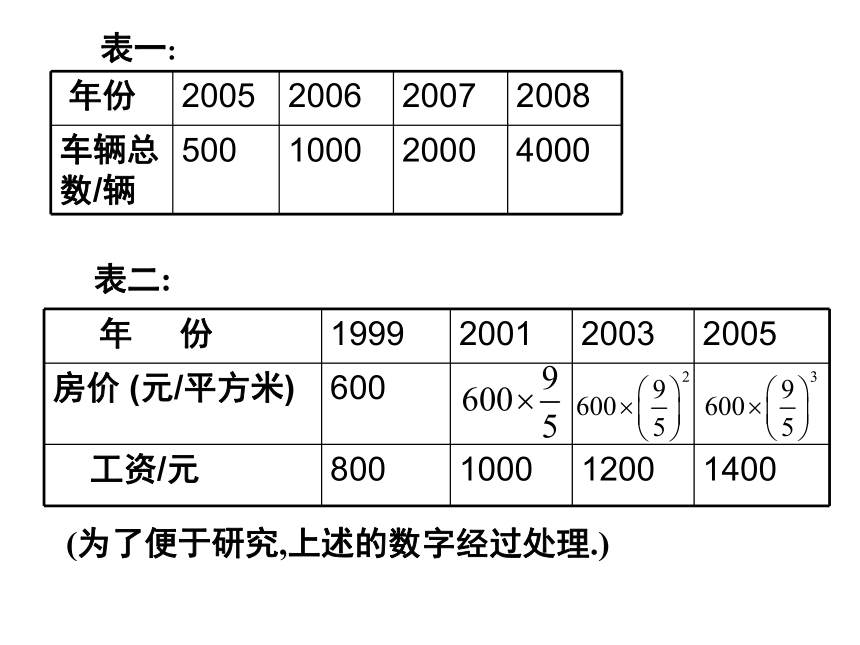
课件18张PPT。 表一:表二:(为了便于研究,上述的数字经过处理.)定义:一般地,如果一个数列从第二项起每
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
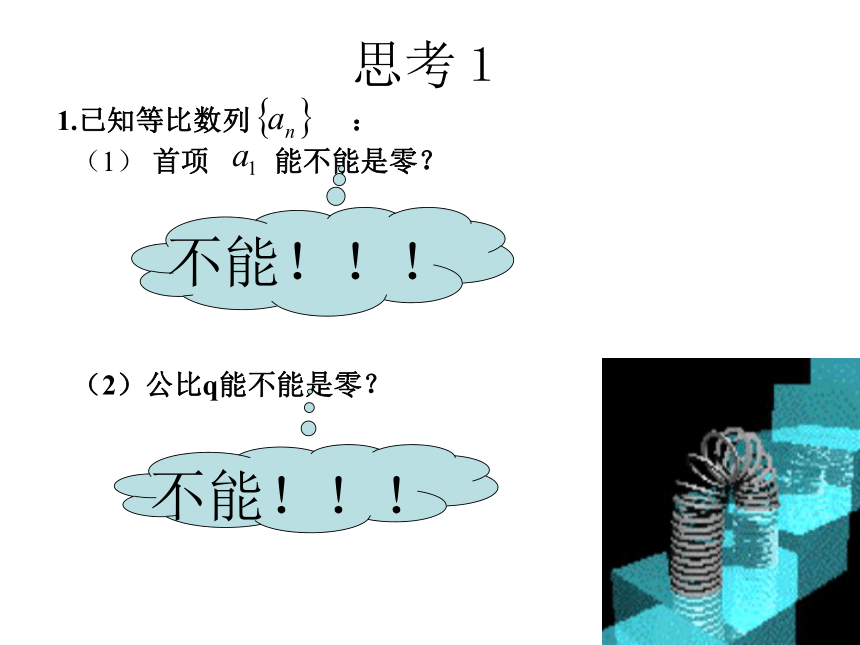
等比数列的公比,公比通常用字母q表示。用数学符号表示(2)公比q能不能是零?(1) 首项 能不能是零?不能!!!不能!!!思考1(正确)(错误)(不是)问题:类比于等差数列,如何从函数角度理解等比数列的通项公式?●●●●●例如:等比数列:1,2,4,8,16,…的图象练习:写出下列数列的通项公式
q=2q=2q=-2q=18278-23-964-24 an,a1,q,n四个基本量中“知三求一”。方程的
思想变:一个等比数列的第3项与第4项分别是12与18, 求它的第1项与第2项及通项公式。问题1:求通项公式an是否一定需要求a1?问题2:从中你能发现a1 、a4、 a2、a3有何关系? 例2 培育水稻新品种,如果第1代得到120粒种子,并且从第1代起,以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这种新品种的种子多少粒(保留两个有效数字)?解:由于每代的种子数是它的前一代种子数的120倍,思考:
如果一辆车停放的面积需4平方米,那么按照上述规律, 请同学们求出几年后车辆将覆盖整个温岭表面?(温岭地表面积960平方公里)计算课堂小结
1.本节课研究了等比数列的概念,得到了通项
公式。
2.注意在研究内容和方法上要与等差数列相类
比。
3.用函数观点与方程思想认识通项公式,
并加以应用。 an+1-an=dd 叫公差q叫公比 an+1=an+d an+1=an q an= a1+(n-1)d an=a1qn-1 an=am+(n-m)d an=amqn-m归纳: 学习知识要善于思考, 思考, 再思考. 我就是靠这个方法成为科学家的。???
--爱因斯坦 祝同学们学习进步!提高题:等比数列通项公式的推导方法一: 递推法方法二: 累积法
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
等比数列的公比,公比通常用字母q表示。用数学符号表示(2)公比q能不能是零?(1) 首项 能不能是零?不能!!!不能!!!思考1(正确)(错误)(不是)问题:类比于等差数列,如何从函数角度理解等比数列的通项公式?●●●●●例如:等比数列:1,2,4,8,16,…的图象练习:写出下列数列的通项公式
q=2q=2q=-2q=18278-23-964-24 an,a1,q,n四个基本量中“知三求一”。方程的
思想变:一个等比数列的第3项与第4项分别是12与18, 求它的第1项与第2项及通项公式。问题1:求通项公式an是否一定需要求a1?问题2:从中你能发现a1 、a4、 a2、a3有何关系? 例2 培育水稻新品种,如果第1代得到120粒种子,并且从第1代起,以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这种新品种的种子多少粒(保留两个有效数字)?解:由于每代的种子数是它的前一代种子数的120倍,思考:
如果一辆车停放的面积需4平方米,那么按照上述规律, 请同学们求出几年后车辆将覆盖整个温岭表面?(温岭地表面积960平方公里)计算课堂小结
1.本节课研究了等比数列的概念,得到了通项
公式。
2.注意在研究内容和方法上要与等差数列相类
比。
3.用函数观点与方程思想认识通项公式,
并加以应用。 an+1-an=dd 叫公差q叫公比 an+1=an+d an+1=an q an= a1+(n-1)d an=a1qn-1 an=am+(n-m)d an=amqn-m归纳: 学习知识要善于思考, 思考, 再思考. 我就是靠这个方法成为科学家的。???
--爱因斯坦 祝同学们学习进步!提高题:等比数列通项公式的推导方法一: 递推法方法二: 累积法
