鲁教版八年级数学上册第4章4.2图形的旋转同步测试题(含答案)
文档属性
| 名称 | 鲁教版八年级数学上册第4章4.2图形的旋转同步测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 158.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-16 07:28:08 | ||
图片预览

文档简介
鲁教版八年级数学上册第4章4.2图形的旋转同步测试题(含答案)
一.选择题(共10小题)
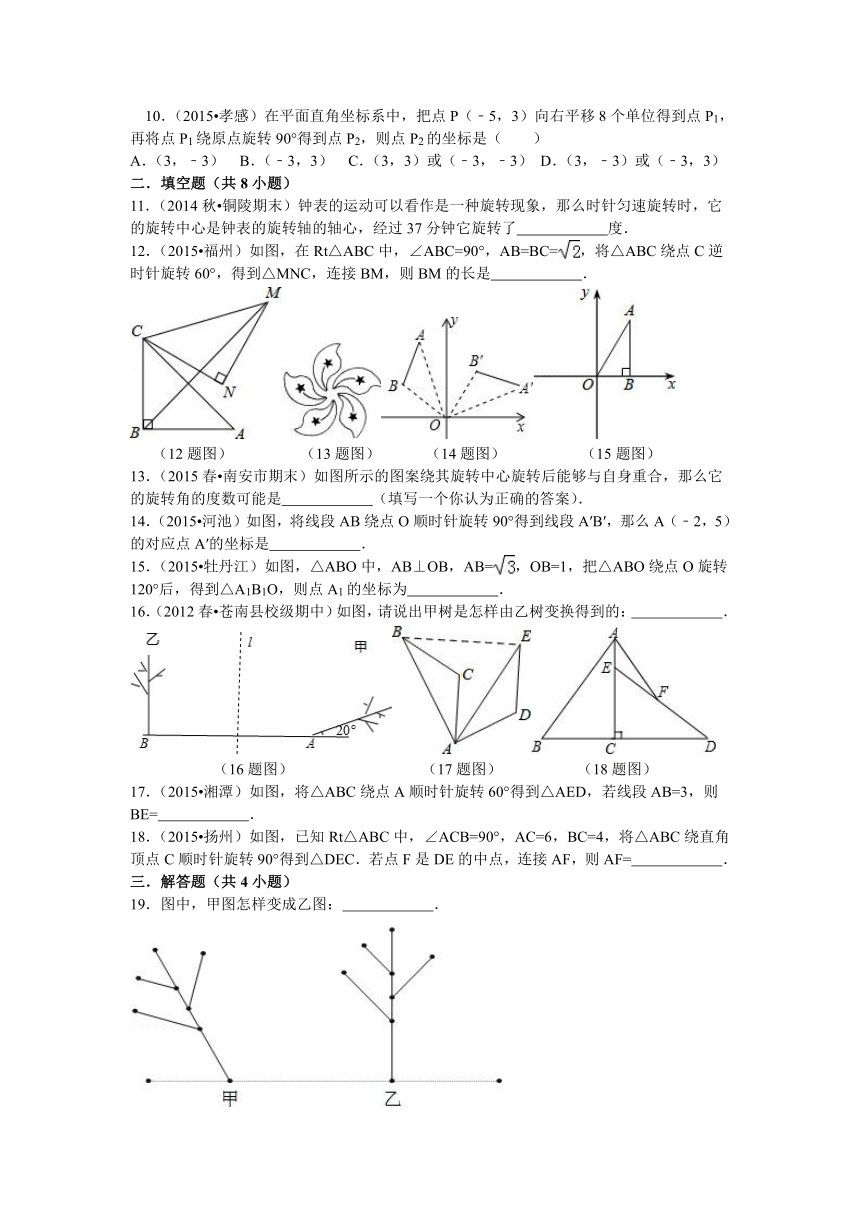
1.(2015 广州)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
2.(2015春 邵阳县期末)下列现象中属于旋转的是( )
A.摩托车在急刹车时向前滑动 B. 拧开水龙头
C.雪橇在雪地里滑动 D. 电梯的上升与下降
3.(2015 德州)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.35° B. 40° C. 50° D. 65°
(3题图) (4题图) (5题图)
4.(2015 哈尔滨)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A.32° B. 64° C. 77° D. 87°
5.(2015 青海)一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
A.105° B. 115° C. 120° D. 135°
6.(2015 浠水县校级模拟)等边三角形ABC绕着它的中心,至少旋转( )度才能与它本身重合.
A.60° B. 120° C. 180° D. 360°
7.(2015 天津)在平面直角坐标系中,把点P(﹣3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B. (2,﹣3) C. (﹣3,﹣2) D. (3,﹣2)
8.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.B. C. D.
9.(2015春 长清区期末)下列说法正确的是( )
A. 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B. 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C. 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D. 在平移和旋转图形中,对应角相等,对应线段相等且平行
10.(2015 孝感)在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
A.(3,﹣3) B.(﹣3,3) C.(3,3)或(﹣3,﹣3) D.(3,﹣3)或(﹣3,3)
二.填空题(共8小题)
11.(2014秋 铜陵期末)钟表的运动可以看作是一种旋转现象,那么时针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过37分钟它旋转了 度.
12.(2015 福州)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
(12题图) (13题图) (14题图) (15题图)
13.(2015春 南安市期末)如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是 (填写一个你认为正确的答案).
14.(2015 河池)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是 .
15.(2015 牡丹江)如图,△ABO中,AB⊥OB,AB=,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为 .
16.(2012春 苍南县校级期中)如图,请说出甲树是怎样由乙树变换得到的: .
(16题图) (17题图) (18题图)
17.(2015 湘潭)如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
18.(2015 扬州)如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
三.解答题(共4小题)
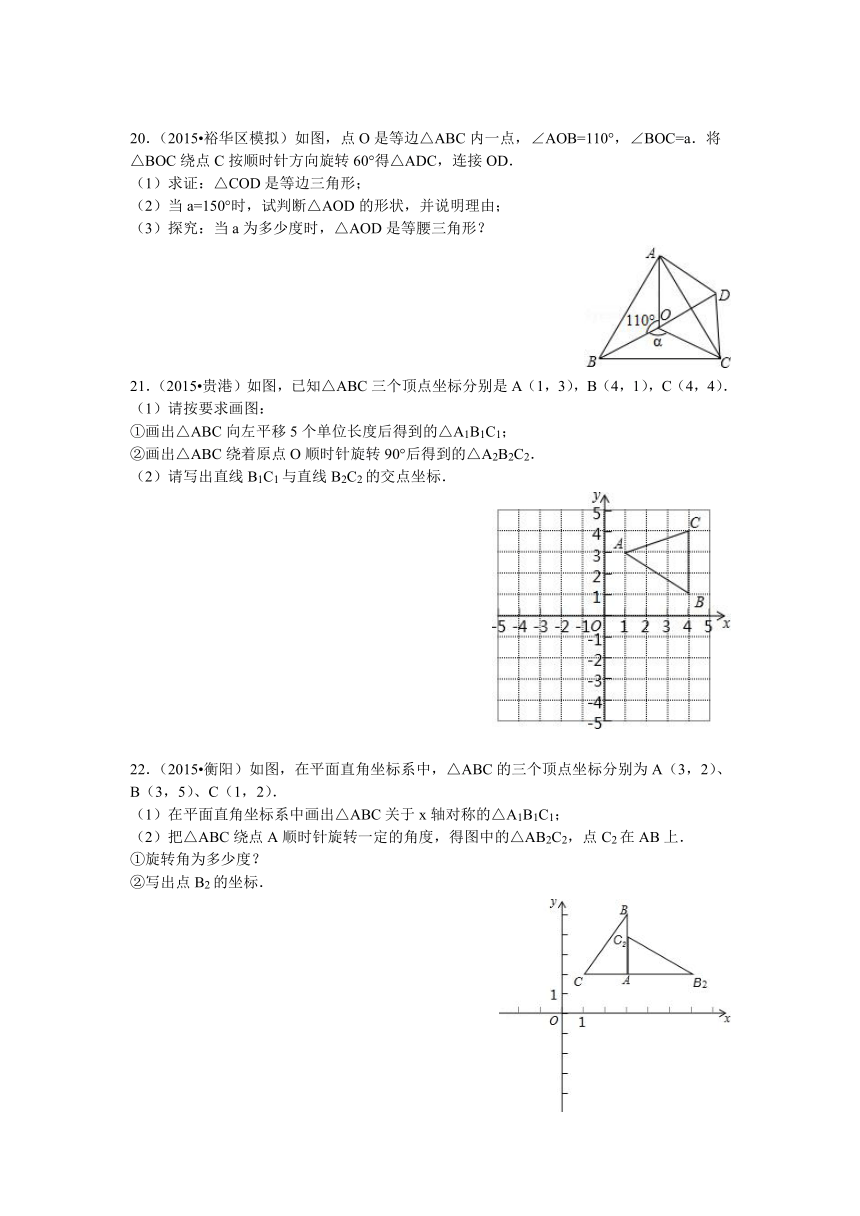
19.图中,甲图怎样变成乙图: .
20.(2015 裕华区模拟)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
21.(2015 贵港)如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
22.(2015 衡阳)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
鲁教版八年级数学上册第4章4.2图形的旋转同步测试题参考答案
一.选择题(共10小题)
1.D 2.B 3.C 4.C 5.C 6.B 7.D 8.C 9.B 10.D
二.填空题(共8小题)
11.18.5 12.+1 13.72°(答案不唯一) 14.A′(5,2)
15.(-2,0)或(1,-)
16.先以直线L为对称轴作轴对称变换,再把所得的像绕点A顺时针旋转70度
17.3 18.5
三.解答题(共4小题)
19、解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
20.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC﹣∠ODC=90°,
∵∠α=150°∠AOB=110°,∠COD=60°,
∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,
∴△AOD不是等腰直角三角形,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,
∴190°﹣α=α﹣60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,
∴α﹣60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α,
∠AOD==120°﹣,
∴190°﹣α=120°﹣,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
21.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)由图形可知:交点坐标为(﹣1,﹣4).
22.解:(1)A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,
(2)①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=,
∵,
∴AB2+AC2=BC2,
∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,
∴旋转角为90°;
②∵AB=AB2=3,
∴CB2=AC+AB2=5,
∴B2的坐标为(6,2).
一.选择题(共10小题)
1.(2015 广州)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
2.(2015春 邵阳县期末)下列现象中属于旋转的是( )
A.摩托车在急刹车时向前滑动 B. 拧开水龙头
C.雪橇在雪地里滑动 D. 电梯的上升与下降
3.(2015 德州)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.35° B. 40° C. 50° D. 65°
(3题图) (4题图) (5题图)
4.(2015 哈尔滨)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A.32° B. 64° C. 77° D. 87°
5.(2015 青海)一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
A.105° B. 115° C. 120° D. 135°
6.(2015 浠水县校级模拟)等边三角形ABC绕着它的中心,至少旋转( )度才能与它本身重合.
A.60° B. 120° C. 180° D. 360°
7.(2015 天津)在平面直角坐标系中,把点P(﹣3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B. (2,﹣3) C. (﹣3,﹣2) D. (3,﹣2)
8.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.B. C. D.
9.(2015春 长清区期末)下列说法正确的是( )
A. 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B. 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C. 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D. 在平移和旋转图形中,对应角相等,对应线段相等且平行
10.(2015 孝感)在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
A.(3,﹣3) B.(﹣3,3) C.(3,3)或(﹣3,﹣3) D.(3,﹣3)或(﹣3,3)
二.填空题(共8小题)
11.(2014秋 铜陵期末)钟表的运动可以看作是一种旋转现象,那么时针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过37分钟它旋转了 度.
12.(2015 福州)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
(12题图) (13题图) (14题图) (15题图)
13.(2015春 南安市期末)如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是 (填写一个你认为正确的答案).
14.(2015 河池)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是 .
15.(2015 牡丹江)如图,△ABO中,AB⊥OB,AB=,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为 .
16.(2012春 苍南县校级期中)如图,请说出甲树是怎样由乙树变换得到的: .
(16题图) (17题图) (18题图)
17.(2015 湘潭)如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
18.(2015 扬州)如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
三.解答题(共4小题)
19.图中,甲图怎样变成乙图: .
20.(2015 裕华区模拟)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
21.(2015 贵港)如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
22.(2015 衡阳)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
鲁教版八年级数学上册第4章4.2图形的旋转同步测试题参考答案
一.选择题(共10小题)
1.D 2.B 3.C 4.C 5.C 6.B 7.D 8.C 9.B 10.D
二.填空题(共8小题)
11.18.5 12.+1 13.72°(答案不唯一) 14.A′(5,2)
15.(-2,0)或(1,-)
16.先以直线L为对称轴作轴对称变换,再把所得的像绕点A顺时针旋转70度
17.3 18.5
三.解答题(共4小题)
19、解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
20.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC﹣∠ODC=90°,
∵∠α=150°∠AOB=110°,∠COD=60°,
∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,
∴△AOD不是等腰直角三角形,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,
∴190°﹣α=α﹣60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,
∴α﹣60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α,
∠AOD==120°﹣,
∴190°﹣α=120°﹣,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
21.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)由图形可知:交点坐标为(﹣1,﹣4).
22.解:(1)A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,
(2)①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=,
∵,
∴AB2+AC2=BC2,
∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,
∴旋转角为90°;
②∵AB=AB2=3,
∴CB2=AC+AB2=5,
∴B2的坐标为(6,2).
