人教版八年级数学上册教学参考课件:12.1全等三角形(共15张PPT)
文档属性
| 名称 | 人教版八年级数学上册教学参考课件:12.1全等三角形(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-16 11:43:11 | ||
图片预览






文档简介
课件15张PPT。12.1 全等三角形 1.理解全等形,全等三角形的概念,会找全等三角形的对应边、对应角和对应顶点.
2.掌握全等三角形的性质,并能进行简单的推理和计算.
3.通过图形变换,培养学生动态观点,研究几何图形. 重点:全等三角形的性质.
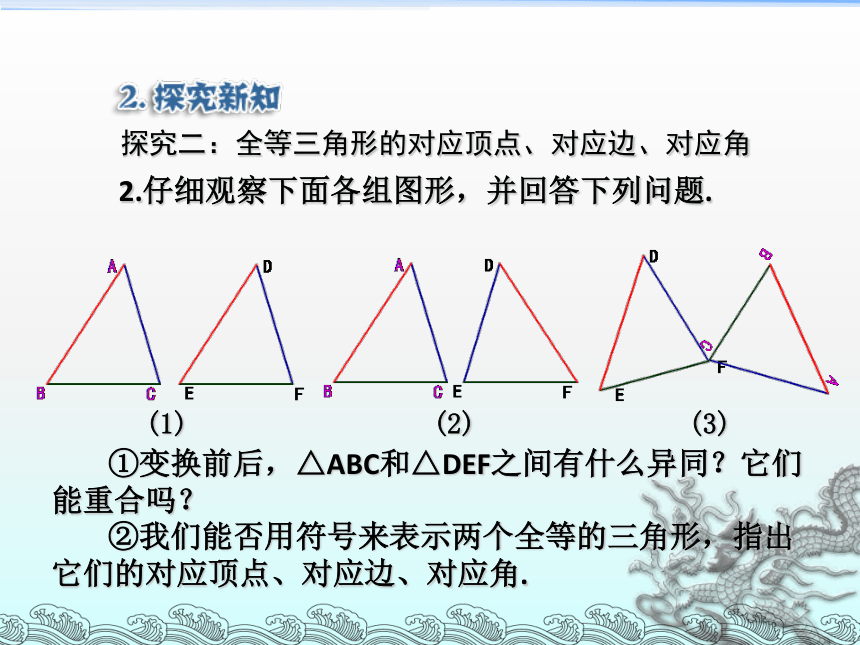
难点:找全等三角形的对应边、对应角、对应顶点. 阅读课本P31-32页内容,了解本节主要内容.重合全等对应边重合相等 请同学们观察下面图片,想一想,它们有什么共同特征? 1.把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板与三角尺的形状、大小是否完全一样?探究一:全等形以及全等三角形的概念 2.仔细观察下面各组图形,并回答下列问题.探究二:全等三角形的对应顶点、对应边、对应角 ①变换前后,△ABC和△DEF之间有什么异同?它们能重合吗? ②我们能否用符号来表示两个全等的三角形,指出它们的对应顶点、对应边、对应角.(1)(2)(3)DC△ABC≌△ADC∠ACB∠A与∠B,∠AOD与∠BOC是对应角,解:OA与OB,OD与OC,
AD与BC是对应边.20 例1:如图,△ABF和△DCE全等,∠A和∠D是对应角,且B与C为对应顶点,写出其相等的对应边和对应角.解析: 由题知∠A和∠D是对应角,则点A与点D是对应顶点,B与C为对应顶点,则F与E是对应顶点.解:∵△ABF≌△DCE,∴对应边是:AB与DC;AF与DE;BF与CE.对应角是:∠A与∠D;∠B与∠C;∠AFB与∠DEC. 例2:如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数是_____. 由翻折知△ABE≌△ADC≌△ABC,从而得∠ABE=∠2,∠ACD=∠3,而∠α=∠EBC+∠DCB=2(∠2+∠3),故只需求∠2+∠3即可. 解析:解:∴△ABE≌△ADC≌△ABC,∵△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的∴∠ABE=∠2,∠ACD=∠3,∴∠α=∠EBC+∠DCB=2(∠2+∠3),∵∠1:∠2:∠3=28:5:3, ∠1+∠2+∠3=180°∴∠2+∠3=40°∴∠α=80°AB95°解:(1)∵△A’B’C’由△ABC平移所得(2)∵由(1)知△ABC≌△A′B′C′(3)∵由(1)知∠B=∠A’B’C’,∴B′C′=BC=3cm; ∠A′=∠A=75°∴△ABC≌△A′B′C′∴ AB∥A′B′. 本课时学习了全等三角形的概念以及表示方法,全等三角形的性质和应用.
2.掌握全等三角形的性质,并能进行简单的推理和计算.
3.通过图形变换,培养学生动态观点,研究几何图形. 重点:全等三角形的性质.
难点:找全等三角形的对应边、对应角、对应顶点. 阅读课本P31-32页内容,了解本节主要内容.重合全等对应边重合相等 请同学们观察下面图片,想一想,它们有什么共同特征? 1.把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板与三角尺的形状、大小是否完全一样?探究一:全等形以及全等三角形的概念 2.仔细观察下面各组图形,并回答下列问题.探究二:全等三角形的对应顶点、对应边、对应角 ①变换前后,△ABC和△DEF之间有什么异同?它们能重合吗? ②我们能否用符号来表示两个全等的三角形,指出它们的对应顶点、对应边、对应角.(1)(2)(3)DC△ABC≌△ADC∠ACB∠A与∠B,∠AOD与∠BOC是对应角,解:OA与OB,OD与OC,
AD与BC是对应边.20 例1:如图,△ABF和△DCE全等,∠A和∠D是对应角,且B与C为对应顶点,写出其相等的对应边和对应角.解析: 由题知∠A和∠D是对应角,则点A与点D是对应顶点,B与C为对应顶点,则F与E是对应顶点.解:∵△ABF≌△DCE,∴对应边是:AB与DC;AF与DE;BF与CE.对应角是:∠A与∠D;∠B与∠C;∠AFB与∠DEC. 例2:如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数是_____. 由翻折知△ABE≌△ADC≌△ABC,从而得∠ABE=∠2,∠ACD=∠3,而∠α=∠EBC+∠DCB=2(∠2+∠3),故只需求∠2+∠3即可. 解析:解:∴△ABE≌△ADC≌△ABC,∵△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的∴∠ABE=∠2,∠ACD=∠3,∴∠α=∠EBC+∠DCB=2(∠2+∠3),∵∠1:∠2:∠3=28:5:3, ∠1+∠2+∠3=180°∴∠2+∠3=40°∴∠α=80°AB95°解:(1)∵△A’B’C’由△ABC平移所得(2)∵由(1)知△ABC≌△A′B′C′(3)∵由(1)知∠B=∠A’B’C’,∴B′C′=BC=3cm; ∠A′=∠A=75°∴△ABC≌△A′B′C′∴ AB∥A′B′. 本课时学习了全等三角形的概念以及表示方法,全等三角形的性质和应用.
