北师版数学必修4正弦余弦函数的图像

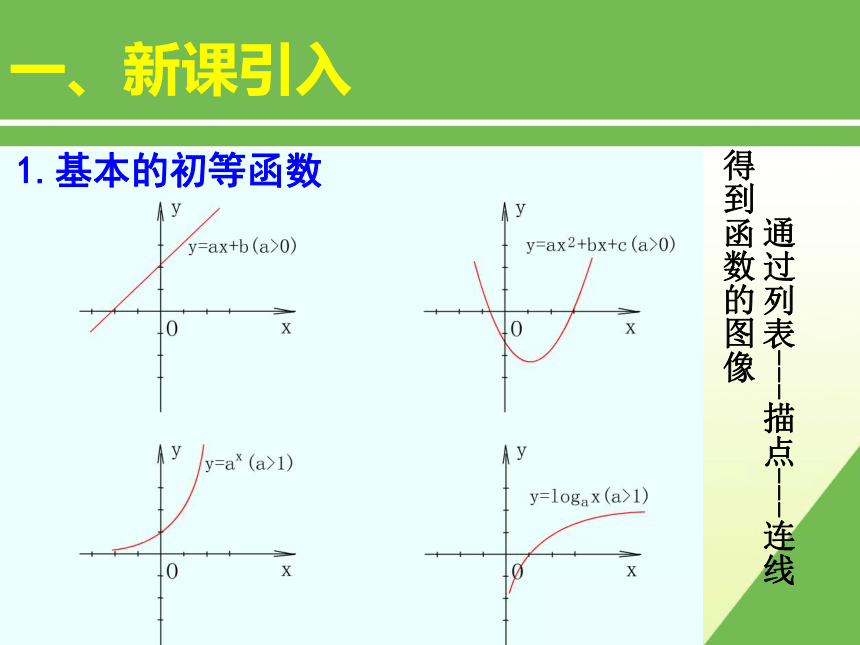
课件18张PPT。一、新课引入1.基本的初等函数 通过列表---描点---连线 得到函数的图像5.2正弦、余弦函数的图像授课人：马广东
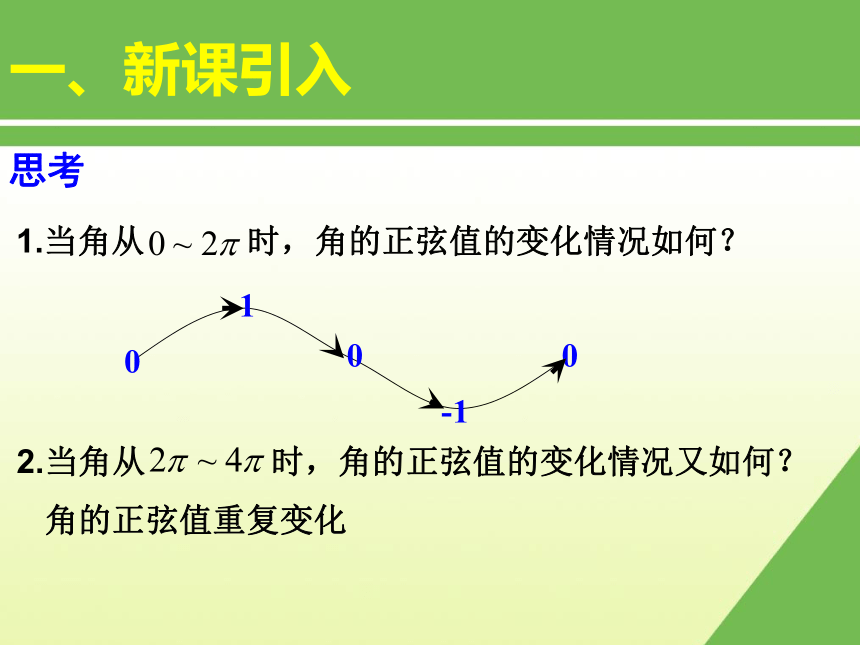
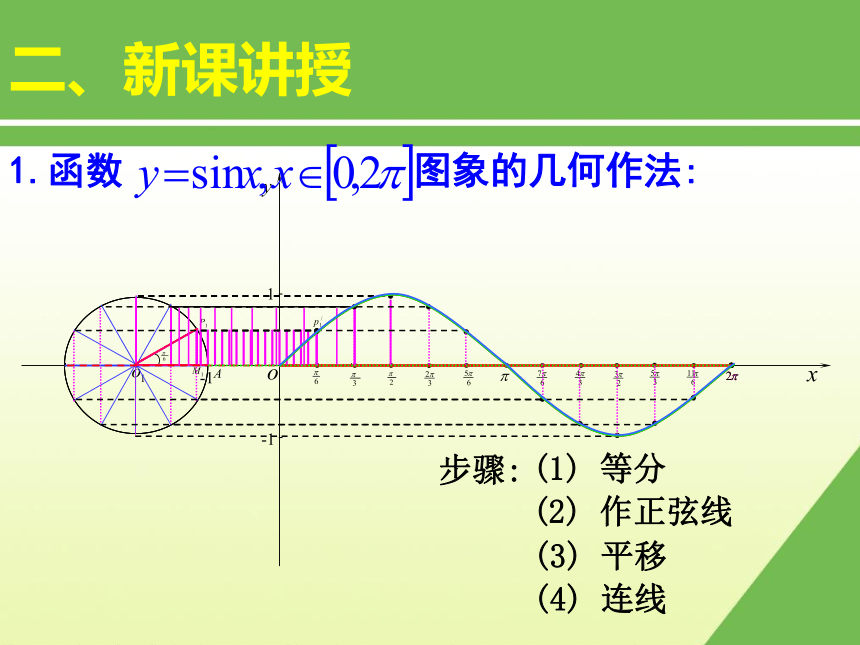
淮北市实验高级中学一、新课引入1.能否用描点法作函数 的图象? 只要能够确定该图象上的点 的坐标，就可以用描点法作出函数图象。而该图象上点的坐标可通过的值查三角函数表得到。2.能否不通过查表得到点 的坐标?思考一、新课引入α的终边　　设任意角α的终边与单位圆相交于点P。过点P做轴的垂线，垂足为M，则有向线段MP叫做角α的正弦线，有向线段OM叫做角α的余弦线。2. 正弦线、余弦线的概念一、新课引入3.在直角坐标系用几何法何作点 由单位圆中的正弦线知识，我们只要知道一个角 的大小，就能用几何方法做出对应的正弦值 的大小。 例如用几何方法在直角坐标系中做出点 ？ 一、新课引入1.当角从 时，角的正弦值的变化情况如何？思考2.当角从 时，角的正弦值的变化情况又如何？角的正弦值重复变化步骤:(1) 等分(2) 作正弦线(3) 平移(4) 连线二、新课讲授1.函数 图象的几何作法:二、新课讲授2.函数 的图象:正弦曲线二、新课讲授2.函数 的图象:二、新课讲授思考:如何作函数 的图象的简图?（在精确度要求不太高时）(0,0)( ,1)( ? ,0)( ,-1)( 2? ,0)五点画图法五点法——简图作法
与x轴的交点图象的最高点图象的最低点(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)二、新课讲授3.五点作图法由于 余弦函数的图像可以通过正弦曲线向左平移

各单位长度而得到．4. 余弦函数的图像二、新课讲授余弦曲线
与x轴的交点图象的最高点图象的最低点二、新课讲授5.五点作图法简图作法
(1) 列表(列出对图象形状起关键作用的五点坐标)(2) 描点(定出五个关键点)(3) 连线(用光滑的曲线顺次连结五个点)例1 画出函数y=1+sinx，x?[0, 2?]的简图： 0 ? 2 ?010-10 1 2 1 0 1 y=sinx，x?[0, 2?]y=1+sinx，x?[0, 2?]步骤：
1.列表
2.描点
3.连线三、例题解析例2 画出函数y= - cosx，x?[0, 2?]的简图： 0 ? 2 ?10-101 -1 0 1 0 -1 y= - cosx，x?[0, 2?]y=cosx，x?[0, 2?]三、例题解析1.作函数 的简图。2.作函数 的简图。四、课堂练习 0 ? 2 ? 5.在同一坐标系内，用五点法分别画出函数
y= sinx，x?[0, 2?] 和 y= cosx，x?[ , ]的简图：y=sinx，x?[0, 2?]y= cosx，x?[ , ] 向左平移 个单位长度100-10 0 ? 四、课堂练习1. 正弦曲线、余弦曲线2.注意与诱导公式、三角函数线等知识的联系y=sinx，x?[0, 2?]y=cosx，x?[0, 2?]五、课堂小结