平行四边形的性质(第1课时)
文档属性
| 名称 | 平行四边形的性质(第1课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-09 00:00:00 | ||
图片预览



文档简介
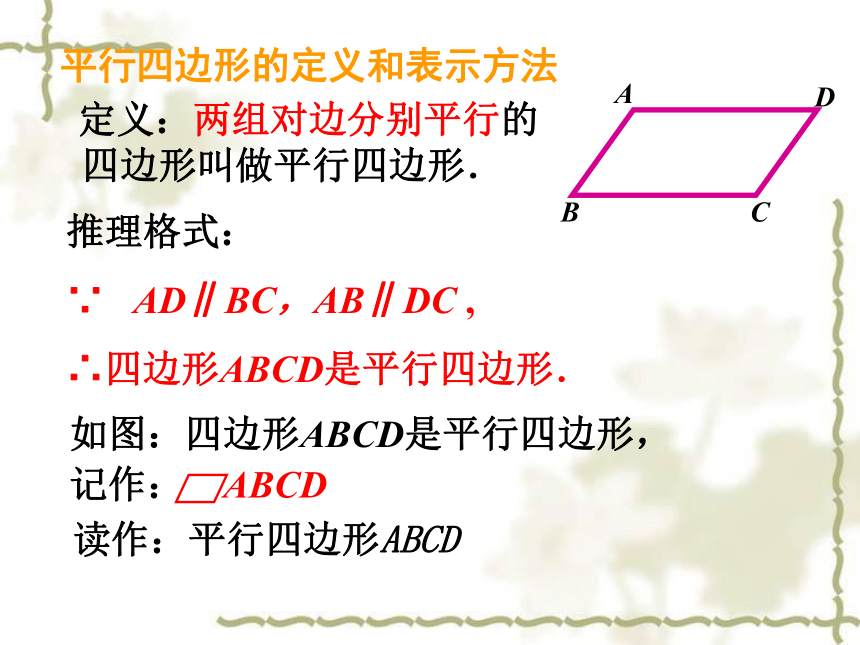
课件13张PPT。19.1 .1平行四边形的性质(第1课时)生活中的平行四边形 定义:两组对边分别平行的四边形叫做平行四边形.平行四边形的定义和表示方法推理格式:
∵ AD∥BC,AB∥DC ,
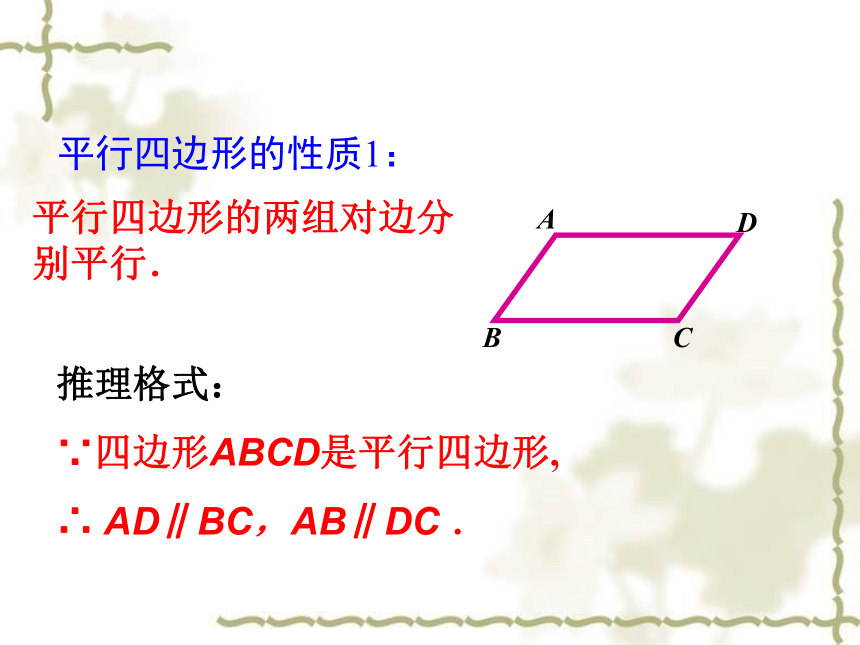
∴四边形ABCD是平行四边形. 读作:平行四边形ABCD平行四边形的两组对边分别平行. 平行四边形的性质1:推理格式:
∵四边形ABCD是平行四边形,
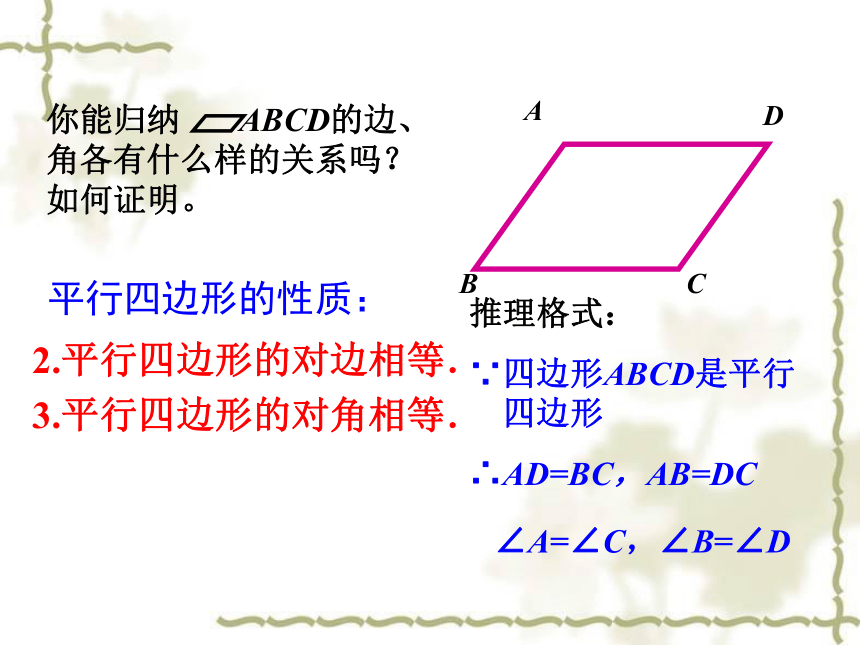
∴ AD∥BC,AB∥DC . 取出两张全等的不等边三角形纸片拼平行四边形,你能拼出几种不同的平行四边形?观察:平行四边形的边、角之间有什么关系?度量一下,是不是和你的猜想一致?2.平行四边形的对边相等.
3.平行四边形的对角相等. 平行四边形的性质:推理格式:
∵四边形ABCD是平行 四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D 已知:
四边形ABCD是平行四边形,
求证:
AD=BC,AB=DC
∠A=∠C,∠B=∠D
利用化归思想把平行四边形转化为两个全等的三角形,证明对边和对角分别相等。解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m例1 如图 ,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 运用所学知识解决问题练习:1.在 ABCD中,AB=5,BC=3,求它的周长。2. 如图 ,在平行四边形ABCD中, ∠A:∠B= 5:4, 求∠C的度数.3、已知如图,在 ABCD中,
求证:①△ABE≌△CDF②AE=CFE、F分别是边BC和AD上的点,且BE=DF。注意:运用平行四边形的性质可证明线段、角相等或三角形全等。对边(平行且)相等.
对角相等.2.平行四边形的性质:1.平行四边形的定义:
两组对边分别平行的
四边形叫做平行四边形.∵四边形ABCD是 平行四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D 课堂小结作业布置
课书 P90,1、2
∵ AD∥BC,AB∥DC ,
∴四边形ABCD是平行四边形. 读作:平行四边形ABCD平行四边形的两组对边分别平行. 平行四边形的性质1:推理格式:
∵四边形ABCD是平行四边形,
∴ AD∥BC,AB∥DC . 取出两张全等的不等边三角形纸片拼平行四边形,你能拼出几种不同的平行四边形?观察:平行四边形的边、角之间有什么关系?度量一下,是不是和你的猜想一致?2.平行四边形的对边相等.
3.平行四边形的对角相等. 平行四边形的性质:推理格式:
∵四边形ABCD是平行 四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D 已知:
四边形ABCD是平行四边形,
求证:
AD=BC,AB=DC
∠A=∠C,∠B=∠D
利用化归思想把平行四边形转化为两个全等的三角形,证明对边和对角分别相等。解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m例1 如图 ,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 运用所学知识解决问题练习:1.在 ABCD中,AB=5,BC=3,求它的周长。2. 如图 ,在平行四边形ABCD中, ∠A:∠B= 5:4, 求∠C的度数.3、已知如图,在 ABCD中,
求证:①△ABE≌△CDF②AE=CFE、F分别是边BC和AD上的点,且BE=DF。注意:运用平行四边形的性质可证明线段、角相等或三角形全等。对边(平行且)相等.
对角相等.2.平行四边形的性质:1.平行四边形的定义:
两组对边分别平行的
四边形叫做平行四边形.∵四边形ABCD是 平行四边形
∴AD=BC,AB=DC
∠A=∠C,∠B=∠D 课堂小结作业布置
课书 P90,1、2
