【新课堂】北师大版数学九年级下册 2.1 二次函数 教案(表格式)
文档属性
| 名称 | 【新课堂】北师大版数学九年级下册 2.1 二次函数 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 22.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览



文档简介
北师大版数学九年级下册2.1二次函数
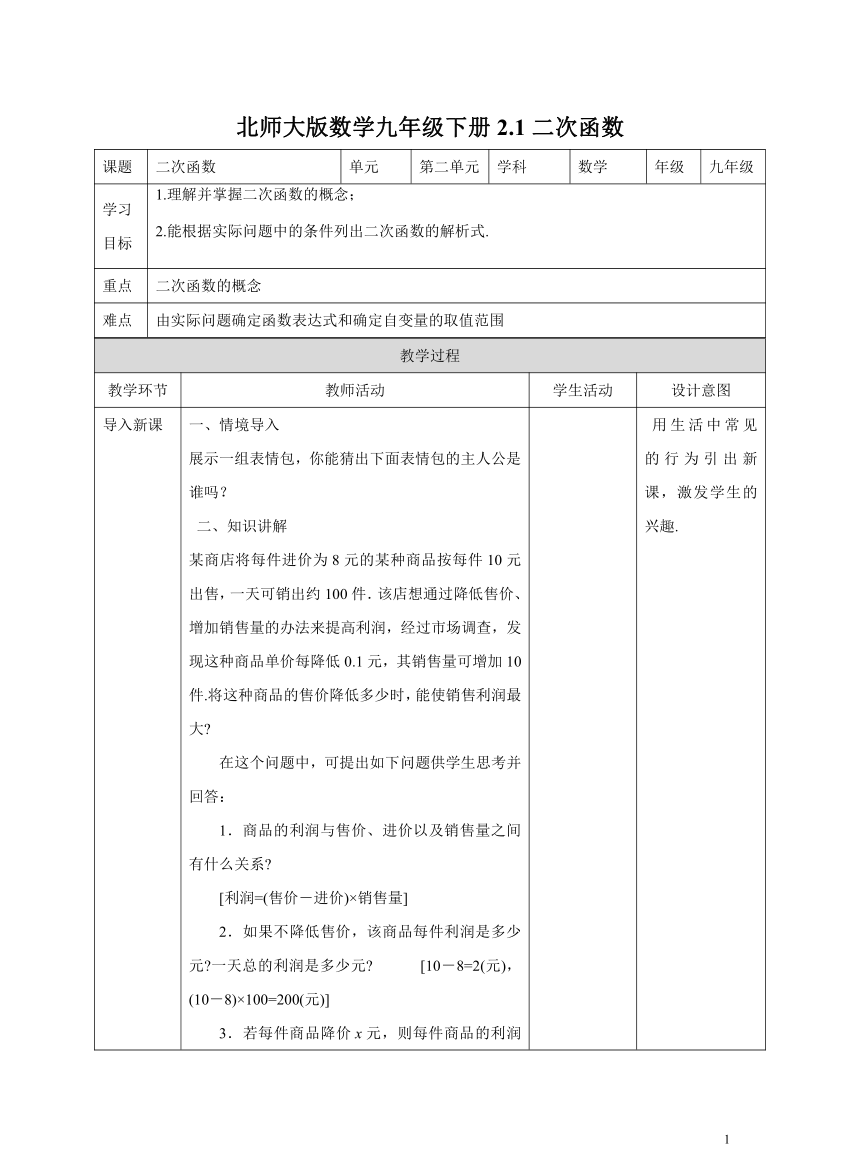
课题 二次函数 单元 第二单元 学科 数学 年级 九年级
学习 目标 1.理解并掌握二次函数的概念; 2.能根据实际问题中的条件列出二次函数的解析式.
重点 二次函数的概念
难点 由实际问题确定函数表达式和确定自变量的取值范围
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、情境导入 展示一组表情包,你能猜出下面表情包的主人公是谁吗? 二、知识讲解 某商店将每件进价为8元的某种商品按每件10元出售,一天可销出约100件.该店想通过降低售价、增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加10件.将这种商品的售价降低多少时,能使销售利润最大 在这个问题中,可提出如下问题供学生思考并回答: 1.商品的利润与售价、进价以及销售量之间有什么关系 [利润=(售价-进价)×销售量] 2.如果不降低售价,该商品每件利润是多少元 一天总的利润是多少元 [10-8=2(元),(10-8)×100=200(元)] 3.若每件商品降价x元,则每件商品的利润是多少元 一天可销售约多少件商品 [(10-8-x);(100+100x)] 4.x的值是否可以任意取 如果不能任意取,请求出它的范围, [x的值不能任意取,其范围是0≤x≤2] 5.若设该商品每天的利润为y元,求y与x的函数关系式. [y=(10-8-x) (100+100x)(0≤x≤2)] 将函数关系式y=x(20-2x)(0 <x <10=化为: y=-2x2+20x (0<x<10)…(1) 将函数关系式y=(10-8-x)(100+100x)(0≤x≤2)化为: y=-100x2+100x+200 (0≤x≤2)…(2) 用生活中常见的行为引出新课,激发学生的兴趣.
讲授新课 一、 师:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的. 设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款额是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税). 想一想: (1)已知矩形的周长为40 cm,它的面积可能是100 cm2吗?可能是75 cm2吗?还可能是多少?你能表示这个矩形的面积与其一边长的关系吗? 解:设其中一边为 x cm,面积为y cm2,则 y= x(20-x)=-x2+20x (2)两数的和是20,设其中一个数是x,你能写出这两数之积y的表达式吗? 解: y= x(20-x)=-x2+20x 师:我们刚才推导出来的关系式 y=100x2+200x+100中分析出y是x的函数,你能说出它的结构特点吗? 师,你能归纳出二次函数的定义吗?它的一般表达式是怎样的? 师:为什么 a≠ 0? 概念中的b和c可以为0吗?表达式应该怎么写?它们还是二次函数吗? 师:根据刚才我们分析得到的,我们总结出关于二次函数应该注意: (1)关于x的代数式一定是整式,a,b,c是常数,且a≠ 0. (2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项. (3)判断一个函数是不是二次函数,先把它化成一般形式. 师:函数y = ax2 + bx + c( a, b, c 是常数),当a, b, c 满足什么条件时: 它是二次函数? 它是一次函数? 它是正比例函数? 师:同学们回答的非常正确,下面我们来检验一下大家的掌握情况. 1.下列函数中( x, t 是自变量), 哪些是二次函数? y = -12+ 3x2, y = 12x2- x3+ 25, y = 22 + 2x, s = 1 + t + 5t2. 2. 圆的半径是 1 cm, 假设半径增加 x cm 时, 圆的面积增加 y cm2. ( 1) 写出 y 与 x 之间的关系式; ( 2) 当圆的半径分别增加 1 cm, cm, 2 cm 时, 圆的面积各增加多少? 3. m取何值时,函数y=(m+1)xm2-2m-1+(m-3)x+m是二次函数? 4.对于y=(m+3)xm2-7 (1)m取什么值时,此函数是正比例函数? (2) m取什么值时,此函数是反比例函数? (3) m取什么值时,此函数是二次函数? 4.某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空余.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间的房价每天不得高于340元.设每个房间的房价每天增加x元(x为10的整数倍). (1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围; (2)设宾馆一天的利润为w元,求w与x的函数关系式; 二、巩固练习 完成课件内容 生:y关于x的代数式是整式且等式的右边最高次数为2 生:一般地,形如y = ax2 + bx + c( a, b, c 是常数, a≠ 0) 的函数叫做 x 的二次函数 . 生:若 a≠ 0,就没有二次项了,就不是二次函数了. 生:可以 当b=0时, y = ax2 + c 当c=0时, y = ax2 + bx 当b=0,c=0时, y = ax2 它们都是二次函数. 生:(1)a≠ 0 (2) a=0, b≠ 0 (3) a=0, b≠ 0 , c =0 生:完成相应练习题 由简单到复杂,逐步推进的设计问题,同时让学生初步体会到问题中所蕴含的函数关系. 通过交流讨论,培养学生思维的严密性和灵活性,让学生体验在交流中收益的乐趣.增强自信心,锻炼学生的语言表达能力. 培养学生分析、比较、归纳的能力. 让学生从丰富的背景中体会函数模型的意义,在大量模型的基础上归纳出二次函数的基本形式 通过练习巩固新知
课堂小结
板书 二次函数 一、二次函数的定义 y = ax2 + bx + c( a, b, c 是常数, a≠ 0) 注意: (1)关于x的代数式整式,a≠ 0. (2)等式的右边最高次数为2 (3)先函数化成一般形式,再判断是不是二次函数. 二、二次函数的特殊形式 当b=0时, y = ax2 + c 当c=0时, y = ax2 + bx 当b=0,c=0时, y = ax2 函数y = ax2 + bx + c( a, b, c 是常数), (1)a≠ 0时它是二次函数; (2)a=0, b≠ 0时它是一次函数; (3)a=0, b≠ 0 , c =0它是正比例函数.
1
课题 二次函数 单元 第二单元 学科 数学 年级 九年级
学习 目标 1.理解并掌握二次函数的概念; 2.能根据实际问题中的条件列出二次函数的解析式.
重点 二次函数的概念
难点 由实际问题确定函数表达式和确定自变量的取值范围
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、情境导入 展示一组表情包,你能猜出下面表情包的主人公是谁吗? 二、知识讲解 某商店将每件进价为8元的某种商品按每件10元出售,一天可销出约100件.该店想通过降低售价、增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加10件.将这种商品的售价降低多少时,能使销售利润最大 在这个问题中,可提出如下问题供学生思考并回答: 1.商品的利润与售价、进价以及销售量之间有什么关系 [利润=(售价-进价)×销售量] 2.如果不降低售价,该商品每件利润是多少元 一天总的利润是多少元 [10-8=2(元),(10-8)×100=200(元)] 3.若每件商品降价x元,则每件商品的利润是多少元 一天可销售约多少件商品 [(10-8-x);(100+100x)] 4.x的值是否可以任意取 如果不能任意取,请求出它的范围, [x的值不能任意取,其范围是0≤x≤2] 5.若设该商品每天的利润为y元,求y与x的函数关系式. [y=(10-8-x) (100+100x)(0≤x≤2)] 将函数关系式y=x(20-2x)(0 <x <10=化为: y=-2x2+20x (0<x<10)…(1) 将函数关系式y=(10-8-x)(100+100x)(0≤x≤2)化为: y=-100x2+100x+200 (0≤x≤2)…(2) 用生活中常见的行为引出新课,激发学生的兴趣.
讲授新课 一、 师:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的. 设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款额是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税). 想一想: (1)已知矩形的周长为40 cm,它的面积可能是100 cm2吗?可能是75 cm2吗?还可能是多少?你能表示这个矩形的面积与其一边长的关系吗? 解:设其中一边为 x cm,面积为y cm2,则 y= x(20-x)=-x2+20x (2)两数的和是20,设其中一个数是x,你能写出这两数之积y的表达式吗? 解: y= x(20-x)=-x2+20x 师:我们刚才推导出来的关系式 y=100x2+200x+100中分析出y是x的函数,你能说出它的结构特点吗? 师,你能归纳出二次函数的定义吗?它的一般表达式是怎样的? 师:为什么 a≠ 0? 概念中的b和c可以为0吗?表达式应该怎么写?它们还是二次函数吗? 师:根据刚才我们分析得到的,我们总结出关于二次函数应该注意: (1)关于x的代数式一定是整式,a,b,c是常数,且a≠ 0. (2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项. (3)判断一个函数是不是二次函数,先把它化成一般形式. 师:函数y = ax2 + bx + c( a, b, c 是常数),当a, b, c 满足什么条件时: 它是二次函数? 它是一次函数? 它是正比例函数? 师:同学们回答的非常正确,下面我们来检验一下大家的掌握情况. 1.下列函数中( x, t 是自变量), 哪些是二次函数? y = -12+ 3x2, y = 12x2- x3+ 25, y = 22 + 2x, s = 1 + t + 5t2. 2. 圆的半径是 1 cm, 假设半径增加 x cm 时, 圆的面积增加 y cm2. ( 1) 写出 y 与 x 之间的关系式; ( 2) 当圆的半径分别增加 1 cm, cm, 2 cm 时, 圆的面积各增加多少? 3. m取何值时,函数y=(m+1)xm2-2m-1+(m-3)x+m是二次函数? 4.对于y=(m+3)xm2-7 (1)m取什么值时,此函数是正比例函数? (2) m取什么值时,此函数是反比例函数? (3) m取什么值时,此函数是二次函数? 4.某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空余.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间的房价每天不得高于340元.设每个房间的房价每天增加x元(x为10的整数倍). (1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围; (2)设宾馆一天的利润为w元,求w与x的函数关系式; 二、巩固练习 完成课件内容 生:y关于x的代数式是整式且等式的右边最高次数为2 生:一般地,形如y = ax2 + bx + c( a, b, c 是常数, a≠ 0) 的函数叫做 x 的二次函数 . 生:若 a≠ 0,就没有二次项了,就不是二次函数了. 生:可以 当b=0时, y = ax2 + c 当c=0时, y = ax2 + bx 当b=0,c=0时, y = ax2 它们都是二次函数. 生:(1)a≠ 0 (2) a=0, b≠ 0 (3) a=0, b≠ 0 , c =0 生:完成相应练习题 由简单到复杂,逐步推进的设计问题,同时让学生初步体会到问题中所蕴含的函数关系. 通过交流讨论,培养学生思维的严密性和灵活性,让学生体验在交流中收益的乐趣.增强自信心,锻炼学生的语言表达能力. 培养学生分析、比较、归纳的能力. 让学生从丰富的背景中体会函数模型的意义,在大量模型的基础上归纳出二次函数的基本形式 通过练习巩固新知
课堂小结
板书 二次函数 一、二次函数的定义 y = ax2 + bx + c( a, b, c 是常数, a≠ 0) 注意: (1)关于x的代数式整式,a≠ 0. (2)等式的右边最高次数为2 (3)先函数化成一般形式,再判断是不是二次函数. 二、二次函数的特殊形式 当b=0时, y = ax2 + c 当c=0时, y = ax2 + bx 当b=0,c=0时, y = ax2 函数y = ax2 + bx + c( a, b, c 是常数), (1)a≠ 0时它是二次函数; (2)a=0, b≠ 0时它是一次函数; (3)a=0, b≠ 0 , c =0它是正比例函数.
1
