6.1单项式与多项式同步练习(含简单答案)青岛版(2012)数学七年级上册
文档属性
| 名称 | 6.1单项式与多项式同步练习(含简单答案)青岛版(2012)数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览



文档简介
6.1单项式与多项式同步练习青岛版(2012)数学七年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列代数式中是二次三项式的是( )
A. B. C. D.
2.多项式的次数和常数项分别是
A.4和5 B.1和5 C.1和 D.4和
3.单项式的系数和次数分别是 ( )
A. B.- C. D.
4.单项式的系数与次数分别是( )
A., B., C., D.,
5.把有理数代入得到,称为第一次操作,再将作为的值代入得到,称为第二次操作,…,若,经过第次操作后得到的是( )
A. B. C. D.8
6.按一定规律排列的单项式:﹣2a3,7a6,﹣12a9,17a12,﹣22a15,….其中第n个单项式是( )
A.(﹣1)n(5n+3)a3n B.(﹣1)n(5n﹣3)a3n
C.(﹣1)n﹣1(5n﹣3)a3n D.(﹣1)n﹣1(5n+3)a3n
7.下面的说法错误的是( )
A.是单项式 B.整数和分数统称为有理数
C.的系数是 D.数轴上的点只能表示整数
8.单项式的次数是( )
A.1 B.2 C.3 D.4
9.下列图形都是由同样大小的黑色三角形按一定规律组成的,其中第①个图形中有1个黑色三角形,第②个图形中有4个黑色三角形,第③个图形中有8个黑色三角形,第④个图形中有13个黑色三角形,…,按此规律排列下去,则第⑦个图形中黑色三角形的个数为( )
A.33 B.34 C.35 D.36
10.下列语句中,错误的是( )
A.是单项式 B.单项式的系数与次数都是
C.单项式的系数是 D.的系数是
二、填空题
11.观察一组数据:,,,,,,…,其中第10个数是 ,这10个数的积是 .
12.读一读:式子“”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为,这里“∑”是求和符号通过对以上材料的阅读,计算 .
13.如图,我们可以发现,每一层三角形的个数与层数有规律,如第1层有1个三角形,第2层有3个三角形,第3层有5个三角形…则第8层的三角形个数为 .
14.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有=3条,如果线段AB上有4个点时,线段总数有=6条,如果线段AB上有5个点时,线段总数共有=10条,……
(1)当线段AB上有6个点时,线段总数共有 条;
(2)某学校七年级共有10个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛的场数是 .
15.单项式的次数是 .
16.多项式的一次项系数、常数项分别是 .
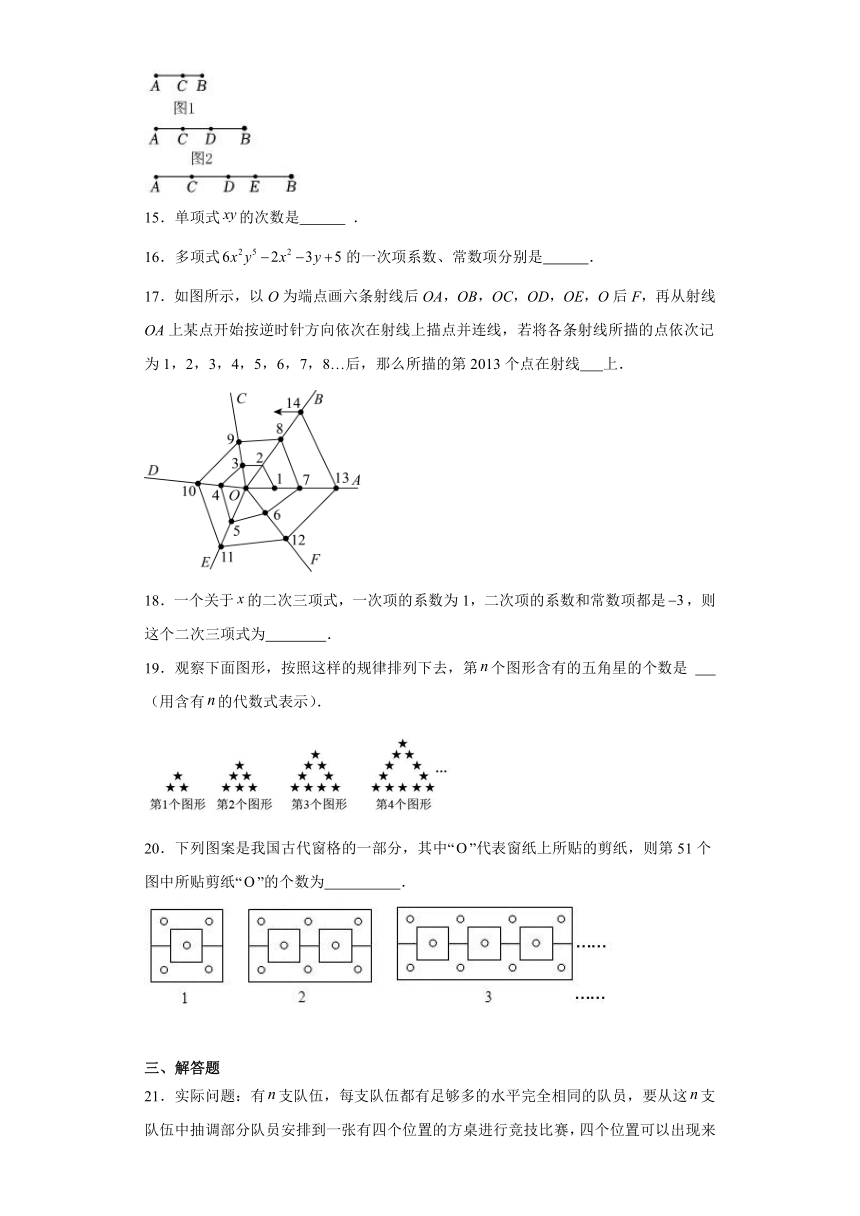
17.如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 上.
18.一个关于的二次三项式,一次项的系数为1,二次项的系数和常数项都是,则这个二次三项式为 .
19.观察下面图形,按照这样的规律排列下去,第个图形含有的五角星的个数是 (用含有的代数式表示).
20.下列图案是我国古代窗格的一部分,其中“”代表窗纸上所贴的剪纸,则第51个图中所贴剪纸“”的个数为 .
三、解答题
21.实际问题:有支队伍,每支队伍都有足够多的水平完全相同的队员,要从这支队伍中抽调部分队员安排到一张有四个位置的方桌进行竞技比赛,四个位置可以出现来自同一队伍的队员,为了防止他们作弊,需要避免同队的队员坐在相邻的座位上.那么一共有多少种不同的安排方法?
问题探究:
探究一:如果有两支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设两支队伍分别为.从①号位开始,我们有2种选择,即队员或队员,②③号位置都只有1种选择(另一支队伍的队员).④号位也只有1种选择.这样就得到了,一共有两种不同的安排方法.
探究二:如果有三支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设三支队伍分别为.让我们运用上面的方法试试①号位置有3种队员可以选择,即队员、队员或队员,②③两个位置选择队员时,我们需要考虑两种不同的情形:
第一种:若②③号位队员来自同一队伍,则②号位有2种选择,③号只有1种选择,④号位会有2中选择,此时会有种安排方法;
第二种:若②③号位队员来自不同的队伍,则②号位有2种选择,③号位只有1种选择,④号位也只有1种选择,此时会有种安排方法.
把上述两种情况的结果加起来得到12+6=18,一共有18种不同的安排方法.
探究三:如果有四支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?(请按照前面的探究方法,描述如果有四支参赛队伍时,会有多少种结果的推算过程)
归纳探究:如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
无论有多少支参赛队伍,我们都要考虑两种情况:②③号位队员来自同一个队伍;②③号位队员来自不同的队伍.
(1)如果有支参赛队伍,①号位有 种队员可以选择,②号位有 种队员可以选择.
(2)若②③号位队员来自同一队伍,则③号位只有1种选择,④号位有 种选择,这样我们就有 种安排方法(结果不需化简);
(3)若②③号位队员来自不同队伍,则③号位有 种选择,④号位有 种选择,这样我们就有 种安排方法.(结果不需化简)
(4)如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有 种不同的安排方法.(结果不需化简)
22.已知代数式是关于x的二次多项式,且二次项的系数为b.如图,在数轴上有点A,B,C三个点,且点A,B,C三点所表示的数分别为a,b,c.已知.
(1)求a,b,c的值;
(2)若动点P,Q分别从C,O两点同时出发,向右运动,且点Q不超过点A.在运动过程中,点E为线段的中点,点为线段的中点,若动点P的速度为每秒2个单位长度,动点Q的速度为每秒3个单位长度,求的值.
(3)若动点P,Q分别自A,B出发的同时出发,都以每秒2个单位长度向左运动,动点M自点C出发,以每秒6个单位长度的速度沿数轴向右运动,设运动时间为t(秒),时,数轴上的有一点N与点M的距离始终为2,且点N在点M的左侧,点T为线段上一点(点T不与点M,N重合),在运动的过程中,若满足(点T不与点P重合),求出此时线段的长度.
23.已知多项式是五次四项式,且单项式的次数与该多项式的次数相同,求,的值.
24.观察下列等式:①,②,③
④,……,回答下列问题:
(1)依照上述规律,直接写出等式:__________________
__________________
(2)求和:
25.按照规律填上所缺的单项式并回答问题:
(1),,,,________,________;
(2)试写出第2018个和第2019个单项式;
(3)试写出第个单项式.
26.观察下面的变形规律:
=1-,, –;
…
解答下面的问题:
(1)若n为正整数,请你猜想=______.
(2)求和: ++…+.
27.将一些半径相同的小圆按如图所示的规律摆放:
(1)填写下表:
图形序号
小圆个数
(2)照这样的规律搭下去,摆个这样的图形需要 个小圆.
参考答案:
1.B
2.D
3.C
4.D
5.B
6.B
7.D
8.C
9.B
10.A
11.
12.
13.15
14. (1)15 (2)45
15.
16.,5;
17.OC
18.
19.
20.155
21.探究三:48种;归纳探究:(1);;(2);;(3);;;(4)
22.(1),,
(2)2
(3)1或
23.,
24.(1),
(2)
25.(1);(2),;(3)
26.(1)(2)
27.(1)24,34(2)2554
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列代数式中是二次三项式的是( )
A. B. C. D.
2.多项式的次数和常数项分别是
A.4和5 B.1和5 C.1和 D.4和
3.单项式的系数和次数分别是 ( )
A. B.- C. D.
4.单项式的系数与次数分别是( )
A., B., C., D.,
5.把有理数代入得到,称为第一次操作,再将作为的值代入得到,称为第二次操作,…,若,经过第次操作后得到的是( )
A. B. C. D.8
6.按一定规律排列的单项式:﹣2a3,7a6,﹣12a9,17a12,﹣22a15,….其中第n个单项式是( )
A.(﹣1)n(5n+3)a3n B.(﹣1)n(5n﹣3)a3n
C.(﹣1)n﹣1(5n﹣3)a3n D.(﹣1)n﹣1(5n+3)a3n
7.下面的说法错误的是( )
A.是单项式 B.整数和分数统称为有理数
C.的系数是 D.数轴上的点只能表示整数
8.单项式的次数是( )
A.1 B.2 C.3 D.4
9.下列图形都是由同样大小的黑色三角形按一定规律组成的,其中第①个图形中有1个黑色三角形,第②个图形中有4个黑色三角形,第③个图形中有8个黑色三角形,第④个图形中有13个黑色三角形,…,按此规律排列下去,则第⑦个图形中黑色三角形的个数为( )
A.33 B.34 C.35 D.36
10.下列语句中,错误的是( )
A.是单项式 B.单项式的系数与次数都是
C.单项式的系数是 D.的系数是
二、填空题
11.观察一组数据:,,,,,,…,其中第10个数是 ,这10个数的积是 .
12.读一读:式子“”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为,这里“∑”是求和符号通过对以上材料的阅读,计算 .
13.如图,我们可以发现,每一层三角形的个数与层数有规律,如第1层有1个三角形,第2层有3个三角形,第3层有5个三角形…则第8层的三角形个数为 .
14.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有=3条,如果线段AB上有4个点时,线段总数有=6条,如果线段AB上有5个点时,线段总数共有=10条,……
(1)当线段AB上有6个点时,线段总数共有 条;
(2)某学校七年级共有10个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛的场数是 .
15.单项式的次数是 .
16.多项式的一次项系数、常数项分别是 .
17.如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 上.
18.一个关于的二次三项式,一次项的系数为1,二次项的系数和常数项都是,则这个二次三项式为 .
19.观察下面图形,按照这样的规律排列下去,第个图形含有的五角星的个数是 (用含有的代数式表示).
20.下列图案是我国古代窗格的一部分,其中“”代表窗纸上所贴的剪纸,则第51个图中所贴剪纸“”的个数为 .
三、解答题
21.实际问题:有支队伍,每支队伍都有足够多的水平完全相同的队员,要从这支队伍中抽调部分队员安排到一张有四个位置的方桌进行竞技比赛,四个位置可以出现来自同一队伍的队员,为了防止他们作弊,需要避免同队的队员坐在相邻的座位上.那么一共有多少种不同的安排方法?
问题探究:
探究一:如果有两支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设两支队伍分别为.从①号位开始,我们有2种选择,即队员或队员,②③号位置都只有1种选择(另一支队伍的队员).④号位也只有1种选择.这样就得到了,一共有两种不同的安排方法.
探究二:如果有三支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设三支队伍分别为.让我们运用上面的方法试试①号位置有3种队员可以选择,即队员、队员或队员,②③两个位置选择队员时,我们需要考虑两种不同的情形:
第一种:若②③号位队员来自同一队伍,则②号位有2种选择,③号只有1种选择,④号位会有2中选择,此时会有种安排方法;
第二种:若②③号位队员来自不同的队伍,则②号位有2种选择,③号位只有1种选择,④号位也只有1种选择,此时会有种安排方法.
把上述两种情况的结果加起来得到12+6=18,一共有18种不同的安排方法.
探究三:如果有四支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?(请按照前面的探究方法,描述如果有四支参赛队伍时,会有多少种结果的推算过程)
归纳探究:如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
无论有多少支参赛队伍,我们都要考虑两种情况:②③号位队员来自同一个队伍;②③号位队员来自不同的队伍.
(1)如果有支参赛队伍,①号位有 种队员可以选择,②号位有 种队员可以选择.
(2)若②③号位队员来自同一队伍,则③号位只有1种选择,④号位有 种选择,这样我们就有 种安排方法(结果不需化简);
(3)若②③号位队员来自不同队伍,则③号位有 种选择,④号位有 种选择,这样我们就有 种安排方法.(结果不需化简)
(4)如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有 种不同的安排方法.(结果不需化简)
22.已知代数式是关于x的二次多项式,且二次项的系数为b.如图,在数轴上有点A,B,C三个点,且点A,B,C三点所表示的数分别为a,b,c.已知.
(1)求a,b,c的值;
(2)若动点P,Q分别从C,O两点同时出发,向右运动,且点Q不超过点A.在运动过程中,点E为线段的中点,点为线段的中点,若动点P的速度为每秒2个单位长度,动点Q的速度为每秒3个单位长度,求的值.
(3)若动点P,Q分别自A,B出发的同时出发,都以每秒2个单位长度向左运动,动点M自点C出发,以每秒6个单位长度的速度沿数轴向右运动,设运动时间为t(秒),时,数轴上的有一点N与点M的距离始终为2,且点N在点M的左侧,点T为线段上一点(点T不与点M,N重合),在运动的过程中,若满足(点T不与点P重合),求出此时线段的长度.
23.已知多项式是五次四项式,且单项式的次数与该多项式的次数相同,求,的值.
24.观察下列等式:①,②,③
④,……,回答下列问题:
(1)依照上述规律,直接写出等式:__________________
__________________
(2)求和:
25.按照规律填上所缺的单项式并回答问题:
(1),,,,________,________;
(2)试写出第2018个和第2019个单项式;
(3)试写出第个单项式.
26.观察下面的变形规律:
=1-,, –;
…
解答下面的问题:
(1)若n为正整数,请你猜想=______.
(2)求和: ++…+.
27.将一些半径相同的小圆按如图所示的规律摆放:
(1)填写下表:
图形序号
小圆个数
(2)照这样的规律搭下去,摆个这样的图形需要 个小圆.
参考答案:
1.B
2.D
3.C
4.D
5.B
6.B
7.D
8.C
9.B
10.A
11.
12.
13.15
14. (1)15 (2)45
15.
16.,5;
17.OC
18.
19.
20.155
21.探究三:48种;归纳探究:(1);;(2);;(3);;;(4)
22.(1),,
(2)2
(3)1或
23.,
24.(1),
(2)
25.(1);(2),;(3)
26.(1)(2)
27.(1)24,34(2)2554
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
