黑龙江省哈尔滨市重点学校2023-2024学年九年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市重点学校2023-2024学年九年级下学期开学考试数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览




文档简介
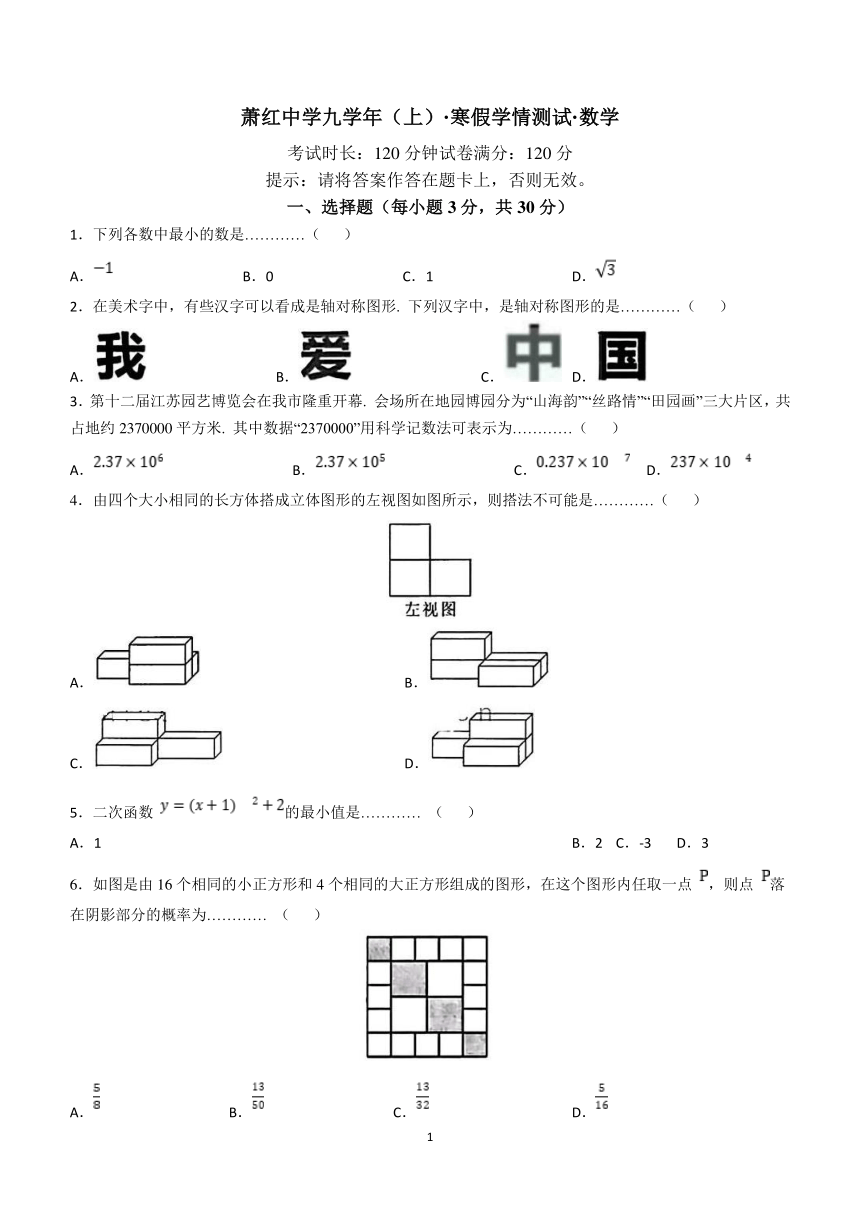
萧红中学九学年(上)·寒假学情测试·数学
考试时长:120分钟试卷满分:120分
提示:请将答案作答在题卡上,否则无效。
一、选择题(每小题3分,共30分)
1.下列各数中最小的数是…………( )
A. B.0 C.1 D.
2.在美术字中,有些汉字可以看成是轴对称图形. 下列汉字中,是轴对称图形的是…………( )
A. B. C. D.
3.第十二届江苏园艺博览会在我市隆重开幕. 会场所在地园博园分为“山海韵”“丝路情”“田园画”三大片区,共占地约2370000平方米. 其中数据“2370000”用科学记数法可表示为…………( )
A. B. C. D.
4.由四个大小相同的长方体搭成立体图形的左视图如图所示,则搭法不可能是…………( )
A. B.
C. D.
5.二次函数 的最小值是………… ( )
A.1 B.2 C.-3 D.3
6.如图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点 ,则点 落在阴影部分的概率为………… ( )
A. B. C. D.
7.下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,……,按此规律排列下去,第⑥个图形中实心圆点的个数为 …………( )
A.18 B.19 C.20 D.21
8.如图,在 A处测得点 在北偏东 方向上,在 B处测得点 在北偏东30°方向上,若 米,则点 到直线 距离 为………… ( )
A.3米 B.米 C.2米 D.1米
9.如图,四边形 是矩形,分别以点 为圆心,线段 长为半径画弧,两弧相交于点 ,连接 若 则 的正切值为…………( )
A. B. C. D.
10.如图1,中,点 从点 A出发沿折线 运动到点 B停止,过点 作 ,垂足为 设点 运动的路径长为 的面积为 ,若 与 的对应关系如图2所示,则 的值为 ( )
A.54 B.52 C.50 D.48
二、填空题(每小题3分,共30分)
11.计算 结果是 .
12.在函数 中,自变量 的取值范围是 .
13.分解因式: .
14.不等式组的解集是 .
15.在平面直角坐标系 中,若点 在反比例函数的图象上,则 (填 ">""="或"").
16.如图,是 的直径,点 在 上,若 ,则 度.
17.一个扇形的面积为 ,其弧长为 ,则它的圆心角度数为 .
18.如图,在 中,分别在 上,,则 的长为 .
19.矩形 中为对角线 的中点,点 在边 上,且 . 当以点 为顶点的三角形是直角三角形时的长为 .
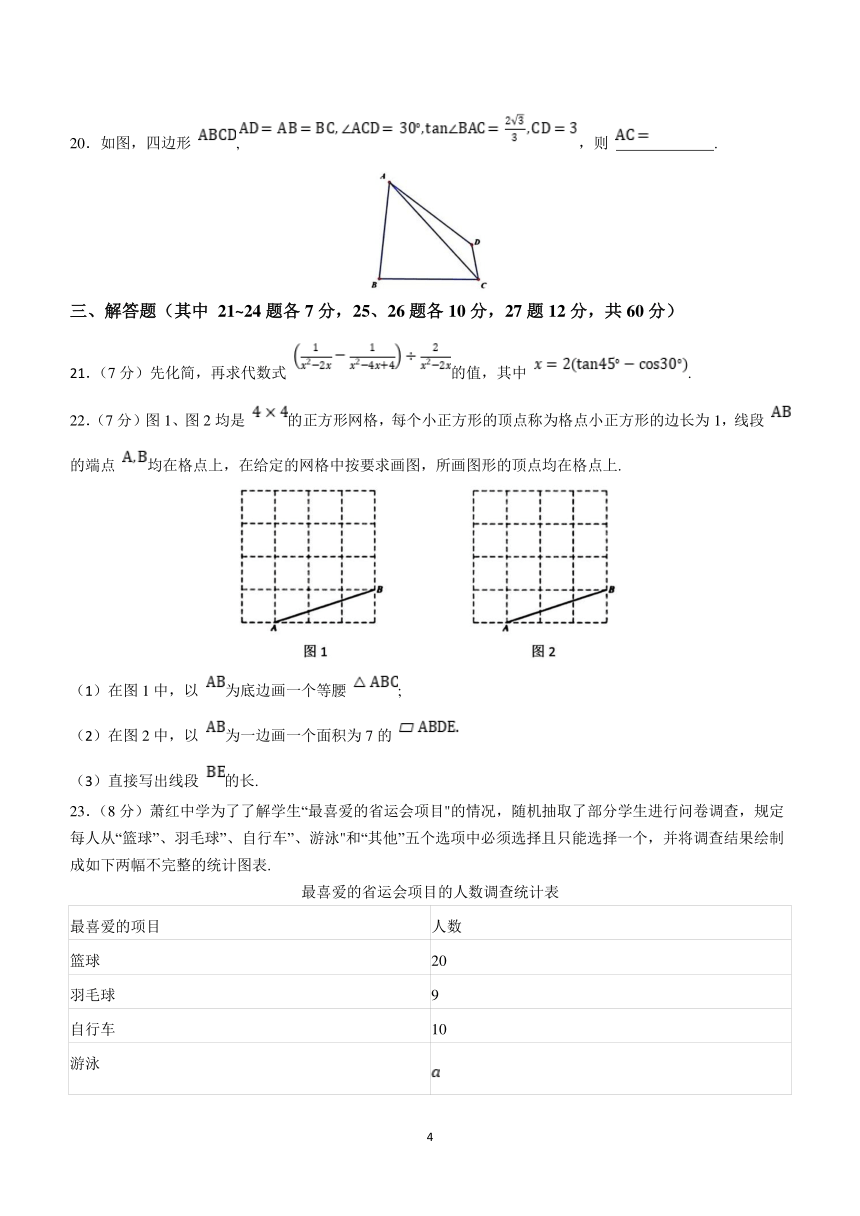
20.如图,四边形 ,,则 .
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.(7分)先化简,再求代数式 的值,其中 .
22.(7分)图1、图2均是 的正方形网格,每个小正方形的顶点称为格点小正方形的边长为1,线段 的端点 均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图1中,以 为底边画一个等腰 ;
(2)在图2中,以 为一边画一个面积为7的
(3)直接写出线段 的长.
23.(8分)萧红中学为了了解学生“最喜爱的省运会项目"的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、羽毛球”、自行车”、游泳"和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表
最喜爱的项目 人数
篮球 20
羽毛球 9
自行车 10
游泳
其他
合计
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 , ;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
24.(8分)如图,中,,过点 作 .
(1)求证 是等腰直角三角形;
(2)延长 至 ,使得 连接并与 的延长线相交于点 求 的度数.
25.(10分)服装店去年10月以每套 元的进价购进一批羽绒服,当月以标价销售,销售额28000元,进入11月份搞促销活动,每件让利 元,这样销售额比10月份增加了11000元,销售量是 月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,服装店决定把剩余羽绒服九折甩货,全部卖掉,这批羽绒服总获利不少于9940元,问这批羽绒服至少购进多少件?
26.(10分)在中,为直径,为弦,弧 弧
(1)如图1,求证:
(2)如图2,过点 D作 的切线,交 延长线于点 ,交 延长线于点 求证:;
(3)如图3,在(2)的条件下,为 上一点,,求 的长.
27.(10分)在平面直角坐标系中,点 0为坐标原点,抛物线 交 轴负半轴于 交正半轴于 交 轴于 .
(1)求抛物线的解析式;
(2)如图1,点 是第三象限抛物线上一点,连接 交 轴于点 设点 横坐标为 ,线段 长为 ,求 与 的函数关系;
(3)如图2,在 (2)的条件下,过点 作 的垂线,交 轴于点 ,垂足为点 为 上一点,连接 若 求点 坐标.
【参考答案】
萧红中学九学年(上)·寒假学情测试·数学
一、选择题(每小题3分,共30分)
1.A 2.C 3.A 4.A 5.B 6.B 7.C 8.B 9.C 10.B
二、填空题(每小题3分,共30分)
11.
12.
13.
14.
15.
16.
17.60°
18.
19.2或
20.
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.
解:原式分
分 分
分
原式分
22.(1)
解:如图所示,
(2)
如图所示,
(3)
23.(1) 50; 11
(2) 72
(3) 解:该校最喜爱的省运会项目是篮球的学生人数为 (人)
24.(1)
证明 ,
,
,
在和中,
,
,
,
,
是等腰直角三角形;
(2)
,
(已证),
,
,
,
四边形 平行四边形,
,
,
等腰直角三角形,
.
25.(1)
设每件羽绒服的标价为元,则 10月份售出 件,
根据题意得:
解得:,
经检验 是原方程的解,
答:每件羽绒服的标价为1400元.
(2)
设这批羽绒服购进件,
10月份售出 (件),11月份售出 (件)
根据题意得:解得 ,
所以至少是99,
答:这批羽绒服至少购进99件.
26.(1) 连 ,得等角,内错角得平行…………2分
(2) 连 ,导角可证…………3分
(3)
延长 交于点 延长 交 于,
证等圆心角,…………1分;证全等,…………1分;导角证 ,…………1分
勾 求 ,得 …………1分
解 求 …………分
27.(1)
点 ,点 (6,0)…………1分
待定系数法求解析式为 …………1分
(2) …………3分
(3)
核心:立倒全等+还原错位角分线
证全等,得 …………1分 构对称,2倍角变等角…………1分 构全等,得BG=KF’…………1分
平八全等导边得…………1分 D(0,-2)法1:求直线解析式与抛 物线相交,求交点坐标法2:求长,用2问结论 定横坐标,在代入解析式求 纵 结论:…………1分
考试时长:120分钟试卷满分:120分
提示:请将答案作答在题卡上,否则无效。
一、选择题(每小题3分,共30分)
1.下列各数中最小的数是…………( )
A. B.0 C.1 D.
2.在美术字中,有些汉字可以看成是轴对称图形. 下列汉字中,是轴对称图形的是…………( )
A. B. C. D.
3.第十二届江苏园艺博览会在我市隆重开幕. 会场所在地园博园分为“山海韵”“丝路情”“田园画”三大片区,共占地约2370000平方米. 其中数据“2370000”用科学记数法可表示为…………( )
A. B. C. D.
4.由四个大小相同的长方体搭成立体图形的左视图如图所示,则搭法不可能是…………( )
A. B.
C. D.
5.二次函数 的最小值是………… ( )
A.1 B.2 C.-3 D.3
6.如图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点 ,则点 落在阴影部分的概率为………… ( )
A. B. C. D.
7.下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,……,按此规律排列下去,第⑥个图形中实心圆点的个数为 …………( )
A.18 B.19 C.20 D.21
8.如图,在 A处测得点 在北偏东 方向上,在 B处测得点 在北偏东30°方向上,若 米,则点 到直线 距离 为………… ( )
A.3米 B.米 C.2米 D.1米
9.如图,四边形 是矩形,分别以点 为圆心,线段 长为半径画弧,两弧相交于点 ,连接 若 则 的正切值为…………( )
A. B. C. D.
10.如图1,中,点 从点 A出发沿折线 运动到点 B停止,过点 作 ,垂足为 设点 运动的路径长为 的面积为 ,若 与 的对应关系如图2所示,则 的值为 ( )
A.54 B.52 C.50 D.48
二、填空题(每小题3分,共30分)
11.计算 结果是 .
12.在函数 中,自变量 的取值范围是 .
13.分解因式: .
14.不等式组的解集是 .
15.在平面直角坐标系 中,若点 在反比例函数的图象上,则 (填 ">""="或"").
16.如图,是 的直径,点 在 上,若 ,则 度.
17.一个扇形的面积为 ,其弧长为 ,则它的圆心角度数为 .
18.如图,在 中,分别在 上,,则 的长为 .
19.矩形 中为对角线 的中点,点 在边 上,且 . 当以点 为顶点的三角形是直角三角形时的长为 .
20.如图,四边形 ,,则 .
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.(7分)先化简,再求代数式 的值,其中 .
22.(7分)图1、图2均是 的正方形网格,每个小正方形的顶点称为格点小正方形的边长为1,线段 的端点 均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图1中,以 为底边画一个等腰 ;
(2)在图2中,以 为一边画一个面积为7的
(3)直接写出线段 的长.
23.(8分)萧红中学为了了解学生“最喜爱的省运会项目"的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、羽毛球”、自行车”、游泳"和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表
最喜爱的项目 人数
篮球 20
羽毛球 9
自行车 10
游泳
其他
合计
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 , ;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
24.(8分)如图,中,,过点 作 .
(1)求证 是等腰直角三角形;
(2)延长 至 ,使得 连接并与 的延长线相交于点 求 的度数.
25.(10分)服装店去年10月以每套 元的进价购进一批羽绒服,当月以标价销售,销售额28000元,进入11月份搞促销活动,每件让利 元,这样销售额比10月份增加了11000元,销售量是 月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,服装店决定把剩余羽绒服九折甩货,全部卖掉,这批羽绒服总获利不少于9940元,问这批羽绒服至少购进多少件?
26.(10分)在中,为直径,为弦,弧 弧
(1)如图1,求证:
(2)如图2,过点 D作 的切线,交 延长线于点 ,交 延长线于点 求证:;
(3)如图3,在(2)的条件下,为 上一点,,求 的长.
27.(10分)在平面直角坐标系中,点 0为坐标原点,抛物线 交 轴负半轴于 交正半轴于 交 轴于 .
(1)求抛物线的解析式;
(2)如图1,点 是第三象限抛物线上一点,连接 交 轴于点 设点 横坐标为 ,线段 长为 ,求 与 的函数关系;
(3)如图2,在 (2)的条件下,过点 作 的垂线,交 轴于点 ,垂足为点 为 上一点,连接 若 求点 坐标.
【参考答案】
萧红中学九学年(上)·寒假学情测试·数学
一、选择题(每小题3分,共30分)
1.A 2.C 3.A 4.A 5.B 6.B 7.C 8.B 9.C 10.B
二、填空题(每小题3分,共30分)
11.
12.
13.
14.
15.
16.
17.60°
18.
19.2或
20.
三、解答题(其中 21~24题各7分,25、26题各10分,27题12分,共60分)
21.
解:原式分
分 分
分
原式分
22.(1)
解:如图所示,
(2)
如图所示,
(3)
23.(1) 50; 11
(2) 72
(3) 解:该校最喜爱的省运会项目是篮球的学生人数为 (人)
24.(1)
证明 ,
,
,
在和中,
,
,
,
,
是等腰直角三角形;
(2)
,
(已证),
,
,
,
四边形 平行四边形,
,
,
等腰直角三角形,
.
25.(1)
设每件羽绒服的标价为元,则 10月份售出 件,
根据题意得:
解得:,
经检验 是原方程的解,
答:每件羽绒服的标价为1400元.
(2)
设这批羽绒服购进件,
10月份售出 (件),11月份售出 (件)
根据题意得:解得 ,
所以至少是99,
答:这批羽绒服至少购进99件.
26.(1) 连 ,得等角,内错角得平行…………2分
(2) 连 ,导角可证…………3分
(3)
延长 交于点 延长 交 于,
证等圆心角,…………1分;证全等,…………1分;导角证 ,…………1分
勾 求 ,得 …………1分
解 求 …………分
27.(1)
点 ,点 (6,0)…………1分
待定系数法求解析式为 …………1分
(2) …………3分
(3)
核心:立倒全等+还原错位角分线
证全等,得 …………1分 构对称,2倍角变等角…………1分 构全等,得BG=KF’…………1分
平八全等导边得…………1分 D(0,-2)法1:求直线解析式与抛 物线相交,求交点坐标法2:求长,用2问结论 定横坐标,在代入解析式求 纵 结论:…………1分
同课章节目录
