(单元复习讲义)数学好玩(知识精讲+典题精练)-2023-2024学年四年级下册数学重难点培优讲义(含解析)(北师大版)
文档属性
| 名称 | (单元复习讲义)数学好玩(知识精讲+典题精练)-2023-2024学年四年级下册数学重难点培优讲义(含解析)(北师大版) |

|
|
| 格式 | docx | ||
| 文件大小 | 106.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览



文档简介
数学好玩单元复习讲义
1.图形的密铺
【知识点归纳】
用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.
①正多边形密铺:
正六边形可以密铺,因为它的每个内角都是120°度,在每个拼接点处恰好能容纳3个内角;正五边形不可以密铺,因为它的每个内角都是108度,而360°不是108的整数倍,在每个拼接点处的内角不能保证没空隙或重叠现象;除正三角形、正四边形和正六边形外,其它正多边形都不可以密铺平面.
②不可单独密铺的图形:a、所有任意三角形与任意四边形都可以密铺.b、正三角形、正四边形、正六边形可以单独用于平移密铺.c、三对对应边平行的六边形可以单独密铺.
2.烙饼问题
【知识点归纳】
(1)烙饼问题公式:
总时间=饼数×2÷每锅的可烙的数量×烙每面的时间
当时间算出来不为整数时,采用进一法取近似数.如饼数为4,每一锅的只数为3时,根据公式,4×2÷3×1约=3分
(2)深层意义:
烙饼问题只是一种数学思考的方法.其实这种合理安排时间的问题,就是“优化问题”,也是被数学家华罗庚称作“运筹安排”的问题.
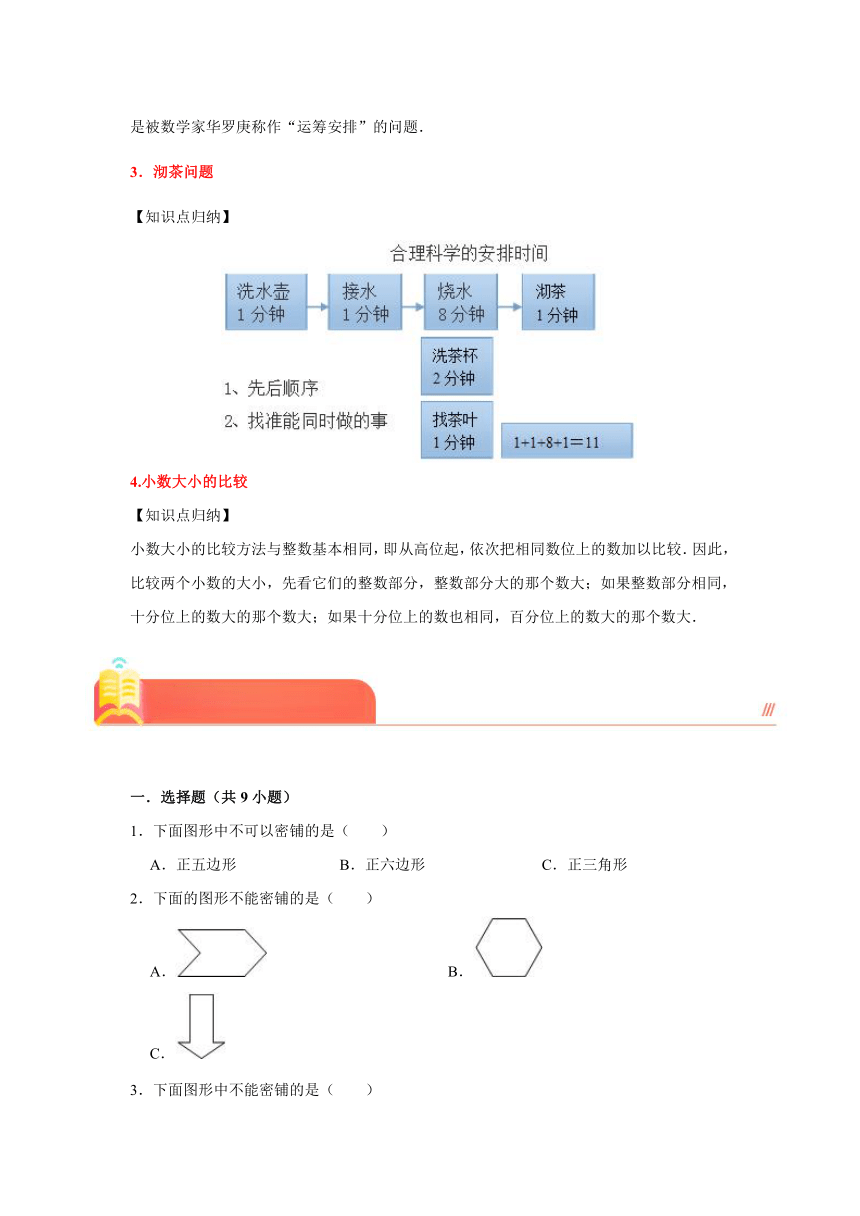
3.沏茶问题
【知识点归纳】
4.小数大小的比较
【知识点归纳】
小数大小的比较方法与整数基本相同,即从高位起,依次把相同数位上的数加以比较.因此,比较两个小数的大小,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大.
一.选择题(共9小题)
1.下面图形中不可以密铺的是( )
A.正五边形 B.正六边形 C.正三角形
2.下面的图形不能密铺的是( )
A. B.
C.
3.下面图形中不能密铺的是( )
A. B. C. D.
4.小明给客人沏茶,接水1分钟,烧水6分钟,洗茶杯2分钟,拿茶叶1分钟,沏茶1分钟。小明为使客人尽快喝到茶,需要合理安排以上事情,最少要( )分钟。
A.11 B.9 C.8 D.10
5.妈妈用平底锅烙5张鸡蛋饼,每次最多只能烙2张鸡蛋饼,两面都要烙,每面2分钟,至少需要( )分钟。
A.12 B.6 C.8 D.10
6.可可爸爸星期六做晚饭,他需要做的事情和所需时间是:洗鱼8分钟,烧鱼15分钟,淘米2分钟,蒸米饭25分钟。可可爸爸做晚饭至少需要( )分钟。
A.25 B.27 C.23 D.35
7.看完《成语故事》这本书,小明需要用1.6小时,小红要用1.5小时。如果两人同时看,谁先看完?( )
A.小明 B.小红 C.同时
8.小红和小英、小兰三人进行60米赛跑,小红用了10.29秒,小英用了12.94秒,小兰用了9.11秒,( )跑得快。
A.小红 B.小兰 C.小英
9.笑笑、淘气和奇思三人进行50米跑步比赛,笑笑用了11.65秒,淘气用了11.29秒,奇思用了11.02秒,( )获得了第一名。
A.笑笑 B.淘气 C.奇思 D.不确定
二.判断题(共5小题)
10.正五边形是轴对称图形,它也能密铺. (判断对错)
11.任何三角形都可以密铺. (判断对错)
12.大于0.1而小于0.3的小数只有1个。 (判断对错)
13.在50米赛跑中小明成绩是9.4秒,小亮是10.5秒,小亮比较快。 (判断对错)
14.用相同的三角形或者相同的四边形都能密铺. (判断对错)
三.填空题(共5小题)
15.100米赛跑,小东的成绩是16.7秒,小明的成绩是16秒,小方的成绩是16.3秒, 的成绩好。
16.明明拖地用8分钟,烧水用10分钟,接水用1分钟,做完这些事情他至少要 分钟。
17.在三角形、平行四边形、正六边形、正八边形中,不能单独密铺的是 。
18.除了长方形、正方形和梯形之外你还知道能够密铺的多边形有 、 .
19.四位同学的50米跑的成绩分别是:小李8.05秒,小亮8.43秒,小唐9.07秒,小秋8.9秒。第一名是 ,第三名是 。
四.解答题(共5小题)
20.下面哪个图形不能密铺?在序号上打“√”.
①长方形 ②正方形 ③梯形 ④正五边形.
21.你知道哪些图形可以密铺吗?请你在可以密铺的图形下面打上勾.
22.小玲感冒了,吃完药后要赶快休息。她应该如何合理安排左边的事情?
找杯子倒开水 1分钟
找感冒药 1分钟
量体温 5分钟
等开水变温 6分钟
23.世界部分国家首都的人均绿地面积情况如表。
国家 首都 人均绿地面积(平方米)
美国 华盛顿 47.75
英国 伦敦 22.86
德国 柏林 50.02
中国 北京 8.18
朝鲜 平壤 47.36
请将上面5个数按从小到大的顺序排列。
< < < < 。
24.姐姐要做“红烧鱼”,你能帮姐姐设计一下,让他们尽早开饭.
数学好玩单元复习讲义
参考答案与试题解析
一.选择题(共9小题)
1.【答案】A
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:A、正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;
B、正六边形的每个内角是120°,能整除360°,能密铺;
C、正三角形的每个内角是60°,能整除360°,能密铺.
故选:A.
【点评】本题考查了平面镶嵌(密铺),用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.
2.【答案】C
【分析】用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.由此可以进行选择.
【解答】解:由密铺的意义可知,
彼此之间不留空隙、不重叠地铺成一片,
因此A、B图形都可以进行密铺,
故选:C.
【点评】本题根据密铺的意义进行选择,即彼此之间不留空隙、不重叠地铺成一片.
3.【答案】B
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:A、因正六边形的每个内角是120°,能整除360°,能密铺,
B、因圆的边线是曲线,不能组成角,所以不能密铺,
C、这个等腰梯形的底角是60°和120°能被360°整除,能密铺,
D、因正三角形的每个内角是60°,能整除360°,能密铺.
故选:B.
【点评】本题的关键是平面图形密铺的知识.
4.【答案】C
【分析】由题意可知,洗茶杯拿茶叶共需1+2=3分钟,烧水的过程需要6分钟,因此可在等待烧水的过程中完成洗茶杯与拿茶叶这两项任务,由此可知,最少要1+6+1=8分钟使客人尽快喝茶。
【解答】解:1+6+1=8(分钟)
答:最少要8分钟使客人尽快喝茶。
故选:C。
【点评】本题考查了学生在生活中利用统筹方法合理安排时间的能力。
5.【答案】D
【分析】烙饼问题公式:总时间=饼数×2÷每锅可烙的数量×烙每面的时间。
【解答】解:5×2÷2×2
=5×2
=10(分钟)
答:至少需要10分钟。
故选:D。
【点评】此题考查了烙饼问题的应用,要熟记公式。
6.【答案】B
【分析】淘米→蒸米饭(同时洗鱼、烧鱼),据此计算时间即可。
【解答】解:2+25=27(分钟)
答:可可爸爸做晚饭至少需要27分钟。
故选:B。
【点评】此题的关键是明确做事顺序,然后再进一步解答。
7.【答案】B
【分析】同样一本书,谁用的时间少,谁看的就快,谁就先看完;所以只要比较二人所用的时间即可得解。
【解答】解:因为1.5小时<1.6小时,所以小红先看完。
故选:B。
【点评】解答此题的关键是明确同样一本书,谁用的时间少,谁看的就快。
8.【答案】B
【分析】根据小数大小的比较方法,谁用的时间少,谁的速度就快,时间多的就慢,解答即可。
【解答】解:因为12.94秒>10.29秒>9.11秒,
小兰用时最少,所以小兰跑得快。
故选:B。
【点评】此题考查了小数大小的比较方法,再比赛中,谁用的时间少,谁的速度就快,就是冠军,时间多的就慢。
9.【答案】C
【分析】根据题意可知,在路程相等的情况下,谁用时最少,谁的速度最快,反之,谁用时最大,谁的速度最慢,据此解答。
【解答】解:因为11.02<11.29<11.65,所以奇思获得了第一名。
故选:C。
【点评】这道题解题的关键是要会正确地进行大小比较和计算。
二.判断题(共5小题)
10.【答案】见试题解答内容
【分析】求出正五边形的每个内角的度数,结合镶嵌的条件:在一个顶点处各正多边形的内角之和为360°即可作出判断.
【解答】解:正五边形是轴对称图形,正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺.
故答案为:×.
【点评】本题考查平面密铺的条件,判断一种正多边形能否镶嵌,要看周角360°能否被一个内角度数整除:若能整除,则能进行平面镶嵌;若不能整除,则不能进行平面镶嵌.
11.【答案】见试题解答内容
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠;(3)连续铺成一片.能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.三角形具备这一特点,因此,若干个完全相同的三角形能密铺.
【解答】解:三角形的内角之是180°,因此,若干个完全相同的三角形的某个角拼在一起,可以是360°,能密铺.
故答案为:√.
【点评】本题考查平面密铺的知识,注意掌握只用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.任意多边形能进行镶嵌,说明它的内角和应能整除360°.
12.【答案】×
【分析】由题意可知要求的小数在0.1和0.3之间,没有说明是几位小数,可以是一位小数、两位小数、三位小数……,所以有无数个小数。
【解答】解:大于0.1而小于0.3的小数有无数个;原题说法错误。
故答案为:×。
【点评】此题考查学生对在两个小数之间有多少个小数的判定方法,应分成一位小数、两位小数、三位小数……,即可确定。
13.【答案】×
【分析】根据相同路程时,时间越短,速度越快,据此解答即可。
【解答】解:9.4<10.5
答:小明比较快。
所以题干说法是错误的。
故答案为:×。
【点评】先比较时间,再比较速度即可。
14.【答案】√
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片. 能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合。长方形、四边形、三角形、正六边形等都具备这一特点,正五边形就不具备这样的特点。
【解答】解:三角形的内角和是180°,能整除360°,可以密铺;
四形的内角和是360°,放在同一顶点处4个即能密铺;符合题意,说法正确。
故答案为:√。
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
三.填空题(共5小题)
15.【答案】小明。
【分析】根据题意可知,在路程相等的情况下,谁用时最少,谁的速度最快,据此解答。
【解答】解:因为16.7>16.3>16,所以小明的成绩好。
故答案为:小明。
【点评】此题主要考查了小数比较大小的方法的应用,要熟练掌握。
16.【答案】11。
【分析】明明先接水,然后烧水,在烧水的同时拖地。这样可以节省8分钟。
【解答】解:1+10=11(分钟)
答:做完这些事情他至少要11分钟。
故答案为:11。
【点评】此题属于合理安排时间问题,要奔着既节约时间又不使每道工序相矛盾进行解答。
17.【答案】正八边形。
【分析】几何图形密铺成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
【解答】解:三角形的内角和是180°,若干个相同的三角形,能组成一个周角。因此,三角形能密铺;
四边形的内角和是(4﹣2)×180°=360°,若干个相同的平行四边形,能组成一个周角。因此,平行四边形能密铺;
正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处恰好能容纳3个内角。3个正六边形拼在一起时,在公共顶点上的3个角度数的和正好也是360度。因此,正六边形能密铺;
八边形的内角和是(8﹣2)×180°=1080°,1080°÷8°=13°,它的每个内角是1080°÷8=135°,几个135°的角不能围成一个周角。因此,正八边形不能密铺。
即在三角形、平行四边形、正六边形、正八边形中,不能单独密铺的是正八边形。
故答案为:正八边形。
【点评】密铺,即平面图形的镶嵌,指用形状、大小完全相同的几种或几十种平面图形进行拼接,使彼此之间不留空隙、不重叠地铺成一片。判断图形能否密铺的关键是看这个图形的内角和能被360°整除。
18.【答案】见试题解答内容
【分析】学过的可以密铺的图形有长方形、正方形、正三角形、正六边形等,据此解答即可.
【解答】解:除了长方形、正方形和梯形之外你还知道能够密铺的多边形有正三角形、正六边形.
故答案为:正三角形;正六边形.
【点评】本题考查的是密铺知识的运用,掌握图形的特征是解答本题的关键.
19.【答案】小李,小秋。
【分析】小数比较大小,先比较整数部分,整数部分相同,从十分位开始依次比起,相同数位上数字大的数大,四位同学跑的路程相同,都是50米,用的时间越少,速度越快,谁跑的时间最短,谁就是第一名,据此解答即可。
【解答】解:因为8.05<8.43<8.9<9.07,
所以第一名是小李,第三名是小秋。
故答案为:小李,小秋。
【点评】本题主要考查了小数的大小比较以及路程相同的情况下,用的时间越少速度越快。
四.解答题(共5小题)
20.【答案】见试题解答内容
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:(1)长方形的每个内角都是90°,能整除360°,能密铺;
(2)正方形同长方形;
(3)两个相同的梯形4个内角围成360°的角,能密铺;
(4)正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺.
故答案为:
【点评】本题是考查图形的密铺,在平面镶嵌时必须满足密铺,即几个内角合起来必须为360°,而正多边形的每个内角相等,所以必须满足正多边形的一个内角能整除360°.经常见到的图形圆、正五边形不具备这一特征,不能密铺.
21.【答案】见试题解答内容
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片.能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.圆就不具备这样的特点.
【解答】解:根据密铺的图形的特征圆和正五边形不能密铺,其余几个图形都可以密铺.
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
22.【答案】先找杯子倒开水,在等开水变温时量体温、找感冒药。
【分析】先找杯子倒开水,在等开水变温时可以量体温、找感冒药,据此解答即可。
【解答】答:
找杯子倒开水 1分钟 共7分钟
等开水变温 6分钟 量体温 5分钟
找感冒药 1分钟
注:量体温和找感冒药的顺序可调换。
【点评】此题的关键是先求出哪些事可以同时做,然后再进一步解答。
23.【答案】8.18;22.86;47.36;47.75;50.02。
【分析】小数大小的比较:先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上相同,百分位上的数大的那个数就大,以此类推。
【解答】解:8.18<22.86<47.36<47.75<50.02
故答案为:8.18;22.86;47.36;47.75;50.02。
【点评】熟练掌握小数的大小比较方法是解答本题的关键。
24.【答案】见试题解答内容
【分析】由题意得:先杀鱼洗鱼,需要6分钟,再烧鱼20分钟,在烧鱼的同时可以淘米,做米饭;据此列式计算即可.
【解答】解:根据图意设计如下:杀鱼洗鱼6分钟→烧鱼:20分钟(同时淘米,做米饭);
共需要:6+20=26(分钟).
答:最少可以用26分钟就可以开饭.
【点评】此题类题目属于合理安排时间,本着既能节约时间,又不使每项程序相互矛盾是解决问题的主要思想方法.
1.图形的密铺
【知识点归纳】
用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.
①正多边形密铺:
正六边形可以密铺,因为它的每个内角都是120°度,在每个拼接点处恰好能容纳3个内角;正五边形不可以密铺,因为它的每个内角都是108度,而360°不是108的整数倍,在每个拼接点处的内角不能保证没空隙或重叠现象;除正三角形、正四边形和正六边形外,其它正多边形都不可以密铺平面.
②不可单独密铺的图形:a、所有任意三角形与任意四边形都可以密铺.b、正三角形、正四边形、正六边形可以单独用于平移密铺.c、三对对应边平行的六边形可以单独密铺.
2.烙饼问题
【知识点归纳】
(1)烙饼问题公式:
总时间=饼数×2÷每锅的可烙的数量×烙每面的时间
当时间算出来不为整数时,采用进一法取近似数.如饼数为4,每一锅的只数为3时,根据公式,4×2÷3×1约=3分
(2)深层意义:
烙饼问题只是一种数学思考的方法.其实这种合理安排时间的问题,就是“优化问题”,也是被数学家华罗庚称作“运筹安排”的问题.
3.沏茶问题
【知识点归纳】
4.小数大小的比较
【知识点归纳】
小数大小的比较方法与整数基本相同,即从高位起,依次把相同数位上的数加以比较.因此,比较两个小数的大小,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大.
一.选择题(共9小题)
1.下面图形中不可以密铺的是( )
A.正五边形 B.正六边形 C.正三角形
2.下面的图形不能密铺的是( )
A. B.
C.
3.下面图形中不能密铺的是( )
A. B. C. D.
4.小明给客人沏茶,接水1分钟,烧水6分钟,洗茶杯2分钟,拿茶叶1分钟,沏茶1分钟。小明为使客人尽快喝到茶,需要合理安排以上事情,最少要( )分钟。
A.11 B.9 C.8 D.10
5.妈妈用平底锅烙5张鸡蛋饼,每次最多只能烙2张鸡蛋饼,两面都要烙,每面2分钟,至少需要( )分钟。
A.12 B.6 C.8 D.10
6.可可爸爸星期六做晚饭,他需要做的事情和所需时间是:洗鱼8分钟,烧鱼15分钟,淘米2分钟,蒸米饭25分钟。可可爸爸做晚饭至少需要( )分钟。
A.25 B.27 C.23 D.35
7.看完《成语故事》这本书,小明需要用1.6小时,小红要用1.5小时。如果两人同时看,谁先看完?( )
A.小明 B.小红 C.同时
8.小红和小英、小兰三人进行60米赛跑,小红用了10.29秒,小英用了12.94秒,小兰用了9.11秒,( )跑得快。
A.小红 B.小兰 C.小英
9.笑笑、淘气和奇思三人进行50米跑步比赛,笑笑用了11.65秒,淘气用了11.29秒,奇思用了11.02秒,( )获得了第一名。
A.笑笑 B.淘气 C.奇思 D.不确定
二.判断题(共5小题)
10.正五边形是轴对称图形,它也能密铺. (判断对错)
11.任何三角形都可以密铺. (判断对错)
12.大于0.1而小于0.3的小数只有1个。 (判断对错)
13.在50米赛跑中小明成绩是9.4秒,小亮是10.5秒,小亮比较快。 (判断对错)
14.用相同的三角形或者相同的四边形都能密铺. (判断对错)
三.填空题(共5小题)
15.100米赛跑,小东的成绩是16.7秒,小明的成绩是16秒,小方的成绩是16.3秒, 的成绩好。
16.明明拖地用8分钟,烧水用10分钟,接水用1分钟,做完这些事情他至少要 分钟。
17.在三角形、平行四边形、正六边形、正八边形中,不能单独密铺的是 。
18.除了长方形、正方形和梯形之外你还知道能够密铺的多边形有 、 .
19.四位同学的50米跑的成绩分别是:小李8.05秒,小亮8.43秒,小唐9.07秒,小秋8.9秒。第一名是 ,第三名是 。
四.解答题(共5小题)
20.下面哪个图形不能密铺?在序号上打“√”.
①长方形 ②正方形 ③梯形 ④正五边形.
21.你知道哪些图形可以密铺吗?请你在可以密铺的图形下面打上勾.
22.小玲感冒了,吃完药后要赶快休息。她应该如何合理安排左边的事情?
找杯子倒开水 1分钟
找感冒药 1分钟
量体温 5分钟
等开水变温 6分钟
23.世界部分国家首都的人均绿地面积情况如表。
国家 首都 人均绿地面积(平方米)
美国 华盛顿 47.75
英国 伦敦 22.86
德国 柏林 50.02
中国 北京 8.18
朝鲜 平壤 47.36
请将上面5个数按从小到大的顺序排列。
< < < < 。
24.姐姐要做“红烧鱼”,你能帮姐姐设计一下,让他们尽早开饭.
数学好玩单元复习讲义
参考答案与试题解析
一.选择题(共9小题)
1.【答案】A
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:A、正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;
B、正六边形的每个内角是120°,能整除360°,能密铺;
C、正三角形的每个内角是60°,能整除360°,能密铺.
故选:A.
【点评】本题考查了平面镶嵌(密铺),用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.
2.【答案】C
【分析】用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.由此可以进行选择.
【解答】解:由密铺的意义可知,
彼此之间不留空隙、不重叠地铺成一片,
因此A、B图形都可以进行密铺,
故选:C.
【点评】本题根据密铺的意义进行选择,即彼此之间不留空隙、不重叠地铺成一片.
3.【答案】B
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:A、因正六边形的每个内角是120°,能整除360°,能密铺,
B、因圆的边线是曲线,不能组成角,所以不能密铺,
C、这个等腰梯形的底角是60°和120°能被360°整除,能密铺,
D、因正三角形的每个内角是60°,能整除360°,能密铺.
故选:B.
【点评】本题的关键是平面图形密铺的知识.
4.【答案】C
【分析】由题意可知,洗茶杯拿茶叶共需1+2=3分钟,烧水的过程需要6分钟,因此可在等待烧水的过程中完成洗茶杯与拿茶叶这两项任务,由此可知,最少要1+6+1=8分钟使客人尽快喝茶。
【解答】解:1+6+1=8(分钟)
答:最少要8分钟使客人尽快喝茶。
故选:C。
【点评】本题考查了学生在生活中利用统筹方法合理安排时间的能力。
5.【答案】D
【分析】烙饼问题公式:总时间=饼数×2÷每锅可烙的数量×烙每面的时间。
【解答】解:5×2÷2×2
=5×2
=10(分钟)
答:至少需要10分钟。
故选:D。
【点评】此题考查了烙饼问题的应用,要熟记公式。
6.【答案】B
【分析】淘米→蒸米饭(同时洗鱼、烧鱼),据此计算时间即可。
【解答】解:2+25=27(分钟)
答:可可爸爸做晚饭至少需要27分钟。
故选:B。
【点评】此题的关键是明确做事顺序,然后再进一步解答。
7.【答案】B
【分析】同样一本书,谁用的时间少,谁看的就快,谁就先看完;所以只要比较二人所用的时间即可得解。
【解答】解:因为1.5小时<1.6小时,所以小红先看完。
故选:B。
【点评】解答此题的关键是明确同样一本书,谁用的时间少,谁看的就快。
8.【答案】B
【分析】根据小数大小的比较方法,谁用的时间少,谁的速度就快,时间多的就慢,解答即可。
【解答】解:因为12.94秒>10.29秒>9.11秒,
小兰用时最少,所以小兰跑得快。
故选:B。
【点评】此题考查了小数大小的比较方法,再比赛中,谁用的时间少,谁的速度就快,就是冠军,时间多的就慢。
9.【答案】C
【分析】根据题意可知,在路程相等的情况下,谁用时最少,谁的速度最快,反之,谁用时最大,谁的速度最慢,据此解答。
【解答】解:因为11.02<11.29<11.65,所以奇思获得了第一名。
故选:C。
【点评】这道题解题的关键是要会正确地进行大小比较和计算。
二.判断题(共5小题)
10.【答案】见试题解答内容
【分析】求出正五边形的每个内角的度数,结合镶嵌的条件:在一个顶点处各正多边形的内角之和为360°即可作出判断.
【解答】解:正五边形是轴对称图形,正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺.
故答案为:×.
【点评】本题考查平面密铺的条件,判断一种正多边形能否镶嵌,要看周角360°能否被一个内角度数整除:若能整除,则能进行平面镶嵌;若不能整除,则不能进行平面镶嵌.
11.【答案】见试题解答内容
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠;(3)连续铺成一片.能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.三角形具备这一特点,因此,若干个完全相同的三角形能密铺.
【解答】解:三角形的内角之是180°,因此,若干个完全相同的三角形的某个角拼在一起,可以是360°,能密铺.
故答案为:√.
【点评】本题考查平面密铺的知识,注意掌握只用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.任意多边形能进行镶嵌,说明它的内角和应能整除360°.
12.【答案】×
【分析】由题意可知要求的小数在0.1和0.3之间,没有说明是几位小数,可以是一位小数、两位小数、三位小数……,所以有无数个小数。
【解答】解:大于0.1而小于0.3的小数有无数个;原题说法错误。
故答案为:×。
【点评】此题考查学生对在两个小数之间有多少个小数的判定方法,应分成一位小数、两位小数、三位小数……,即可确定。
13.【答案】×
【分析】根据相同路程时,时间越短,速度越快,据此解答即可。
【解答】解:9.4<10.5
答:小明比较快。
所以题干说法是错误的。
故答案为:×。
【点评】先比较时间,再比较速度即可。
14.【答案】√
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片. 能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合。长方形、四边形、三角形、正六边形等都具备这一特点,正五边形就不具备这样的特点。
【解答】解:三角形的内角和是180°,能整除360°,可以密铺;
四形的内角和是360°,放在同一顶点处4个即能密铺;符合题意,说法正确。
故答案为:√。
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
三.填空题(共5小题)
15.【答案】小明。
【分析】根据题意可知,在路程相等的情况下,谁用时最少,谁的速度最快,据此解答。
【解答】解:因为16.7>16.3>16,所以小明的成绩好。
故答案为:小明。
【点评】此题主要考查了小数比较大小的方法的应用,要熟练掌握。
16.【答案】11。
【分析】明明先接水,然后烧水,在烧水的同时拖地。这样可以节省8分钟。
【解答】解:1+10=11(分钟)
答:做完这些事情他至少要11分钟。
故答案为:11。
【点评】此题属于合理安排时间问题,要奔着既节约时间又不使每道工序相矛盾进行解答。
17.【答案】正八边形。
【分析】几何图形密铺成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
【解答】解:三角形的内角和是180°,若干个相同的三角形,能组成一个周角。因此,三角形能密铺;
四边形的内角和是(4﹣2)×180°=360°,若干个相同的平行四边形,能组成一个周角。因此,平行四边形能密铺;
正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处恰好能容纳3个内角。3个正六边形拼在一起时,在公共顶点上的3个角度数的和正好也是360度。因此,正六边形能密铺;
八边形的内角和是(8﹣2)×180°=1080°,1080°÷8°=13°,它的每个内角是1080°÷8=135°,几个135°的角不能围成一个周角。因此,正八边形不能密铺。
即在三角形、平行四边形、正六边形、正八边形中,不能单独密铺的是正八边形。
故答案为:正八边形。
【点评】密铺,即平面图形的镶嵌,指用形状、大小完全相同的几种或几十种平面图形进行拼接,使彼此之间不留空隙、不重叠地铺成一片。判断图形能否密铺的关键是看这个图形的内角和能被360°整除。
18.【答案】见试题解答内容
【分析】学过的可以密铺的图形有长方形、正方形、正三角形、正六边形等,据此解答即可.
【解答】解:除了长方形、正方形和梯形之外你还知道能够密铺的多边形有正三角形、正六边形.
故答案为:正三角形;正六边形.
【点评】本题考查的是密铺知识的运用,掌握图形的特征是解答本题的关键.
19.【答案】小李,小秋。
【分析】小数比较大小,先比较整数部分,整数部分相同,从十分位开始依次比起,相同数位上数字大的数大,四位同学跑的路程相同,都是50米,用的时间越少,速度越快,谁跑的时间最短,谁就是第一名,据此解答即可。
【解答】解:因为8.05<8.43<8.9<9.07,
所以第一名是小李,第三名是小秋。
故答案为:小李,小秋。
【点评】本题主要考查了小数的大小比较以及路程相同的情况下,用的时间越少速度越快。
四.解答题(共5小题)
20.【答案】见试题解答内容
【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
【解答】解:(1)长方形的每个内角都是90°,能整除360°,能密铺;
(2)正方形同长方形;
(3)两个相同的梯形4个内角围成360°的角,能密铺;
(4)正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺.
故答案为:
【点评】本题是考查图形的密铺,在平面镶嵌时必须满足密铺,即几个内角合起来必须为360°,而正多边形的每个内角相等,所以必须满足正多边形的一个内角能整除360°.经常见到的图形圆、正五边形不具备这一特征,不能密铺.
21.【答案】见试题解答内容
【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片.能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合.圆就不具备这样的特点.
【解答】解:根据密铺的图形的特征圆和正五边形不能密铺,其余几个图形都可以密铺.
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
22.【答案】先找杯子倒开水,在等开水变温时量体温、找感冒药。
【分析】先找杯子倒开水,在等开水变温时可以量体温、找感冒药,据此解答即可。
【解答】答:
找杯子倒开水 1分钟 共7分钟
等开水变温 6分钟 量体温 5分钟
找感冒药 1分钟
注:量体温和找感冒药的顺序可调换。
【点评】此题的关键是先求出哪些事可以同时做,然后再进一步解答。
23.【答案】8.18;22.86;47.36;47.75;50.02。
【分析】小数大小的比较:先看它们的整数部分,整数部分大的那个数就大;如果整数部分相同,十分位上的数大的那个数就大;如果十分位上相同,百分位上的数大的那个数就大,以此类推。
【解答】解:8.18<22.86<47.36<47.75<50.02
故答案为:8.18;22.86;47.36;47.75;50.02。
【点评】熟练掌握小数的大小比较方法是解答本题的关键。
24.【答案】见试题解答内容
【分析】由题意得:先杀鱼洗鱼,需要6分钟,再烧鱼20分钟,在烧鱼的同时可以淘米,做米饭;据此列式计算即可.
【解答】解:根据图意设计如下:杀鱼洗鱼6分钟→烧鱼:20分钟(同时淘米,做米饭);
共需要:6+20=26(分钟).
答:最少可以用26分钟就可以开饭.
【点评】此题类题目属于合理安排时间,本着既能节约时间,又不使每项程序相互矛盾是解决问题的主要思想方法.
