6.2.1排列的概念 课件(共17张PPT)
文档属性
| 名称 | 6.2.1排列的概念 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 15:31:38 | ||
图片预览




文档简介
(共17张PPT)
6.2排列与组合
6.2.1排列的概念
复习回顾
问题:前面学习了哪些计数原理?
枚举法、分类加法计数原理、分步乘法汁数原理
问题:解答计数问题的一般思维过程是什么?
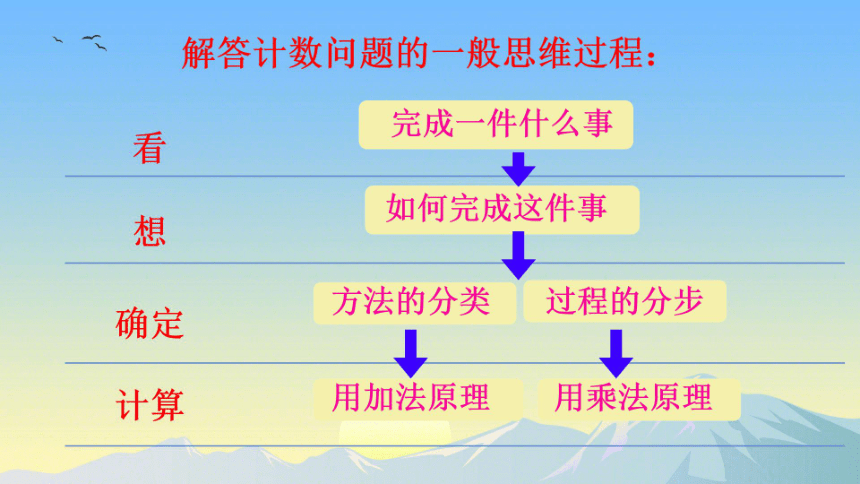
解答计数问题的一殷思维过程:
完成一件什么事
看
如何完成这件事
想
方法的分类
过程的分步
确定
计算
用加法原理
用乘法原理
新课探究
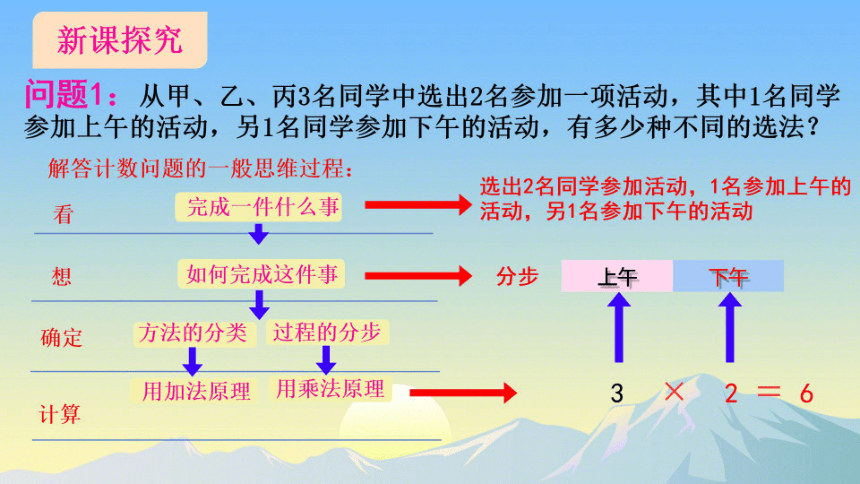
问题1:从甲、
乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
解答计数问题的一般思维过程:
选出2名同学参加活动,1名参加上午的
看
完成一件什么事
活动,另1名参加下午的活动
想
如何完成这件事
分步
上午
下午
确定
方法的分类
过程的分步
用加法原理用乘法原理
3X2=6
计算
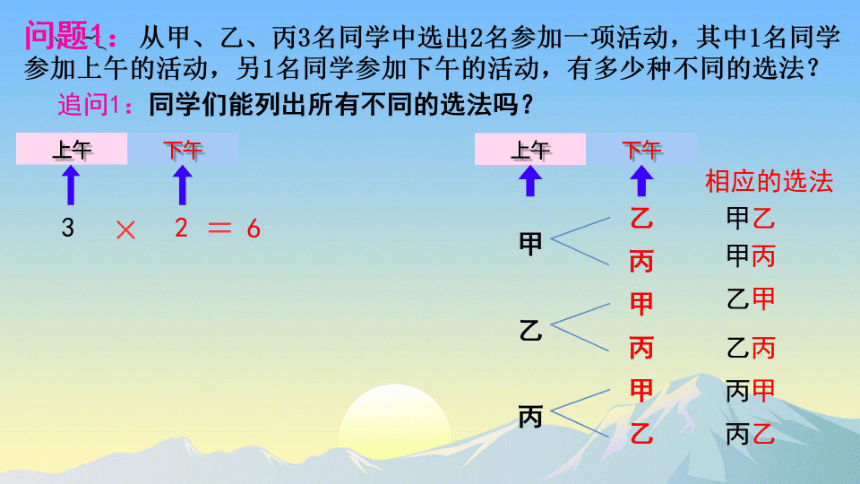
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
追问1:同学们能列出所有不同的选法吗?
上午
下车
上午
下年
个
相应的选法
3
X 2
三6
甲乙
甲
甲丙
乙甲
乙
乙丙甲丙甲乙
乙丙
丙甲
丙
丙乙
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
追问2:问题1中,你能找到哪些关键词?这些关键词体现了什么意思?
参加上午的活动在前,参加下午的活动在后
有先后顺序的安排
追问3:如果把上面问题中被取出的同学叫做元素,那么问题可
以归结为:
从3个不同的元素Q、b、c中任意取出2个,并按一定的顺序
的顺序排成一列,共有多少种不同的排列方法?
所有不同排列是b,ac,ba,bc,ca,cb.
不同的排列方法种数为
3×2=6.
问题2:从1、2、3、4这4个数字中,每次取出3个排成一个三位数,
共可得到多少个不同的三位数?
任务1:请同学们列出所有不同的三位数
百位
个
个
123,124,132,134,142,143,
4×3×2=24
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
通过列举可避免重复和遗漏。
问题2:从1、2、3、4这4个数字中,每次取出3个排成一个三位数,
共可得到多少个不同的三位数?
任务2:类比问题1如果把上面问题中被取出的数字叫做元素,那么
问题2可以归结为:
从4个不同的元素a、b、c、d中任意取出3个,并按百位、
十位、个位的顺序排成一列,共有多少种不同的排列方法?
●所有不同的排列是abc,abd,acb,acd,adb,adc;
bac,bad,bca,bed,bda,
bdc;
cab,cad,cba,
cbd,cda,
edb;
dab,
dac,
dba,
dbc,dca,
dcb.
不排列方法种数4×3×2=24
6.2排列与组合
6.2.1排列的概念
复习回顾
问题:前面学习了哪些计数原理?
枚举法、分类加法计数原理、分步乘法汁数原理
问题:解答计数问题的一般思维过程是什么?
解答计数问题的一殷思维过程:
完成一件什么事
看
如何完成这件事
想
方法的分类
过程的分步
确定
计算
用加法原理
用乘法原理
新课探究
问题1:从甲、
乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
解答计数问题的一般思维过程:
选出2名同学参加活动,1名参加上午的
看
完成一件什么事
活动,另1名参加下午的活动
想
如何完成这件事
分步
上午
下午
确定
方法的分类
过程的分步
用加法原理用乘法原理
3X2=6
计算
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
追问1:同学们能列出所有不同的选法吗?
上午
下车
上午
下年
个
相应的选法
3
X 2
三6
甲乙
甲
甲丙
乙甲
乙
乙丙甲丙甲乙
乙丙
丙甲
丙
丙乙
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学
参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
追问2:问题1中,你能找到哪些关键词?这些关键词体现了什么意思?
参加上午的活动在前,参加下午的活动在后
有先后顺序的安排
追问3:如果把上面问题中被取出的同学叫做元素,那么问题可
以归结为:
从3个不同的元素Q、b、c中任意取出2个,并按一定的顺序
的顺序排成一列,共有多少种不同的排列方法?
所有不同排列是b,ac,ba,bc,ca,cb.
不同的排列方法种数为
3×2=6.
问题2:从1、2、3、4这4个数字中,每次取出3个排成一个三位数,
共可得到多少个不同的三位数?
任务1:请同学们列出所有不同的三位数
百位
个
个
123,124,132,134,142,143,
4×3×2=24
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
通过列举可避免重复和遗漏。
问题2:从1、2、3、4这4个数字中,每次取出3个排成一个三位数,
共可得到多少个不同的三位数?
任务2:类比问题1如果把上面问题中被取出的数字叫做元素,那么
问题2可以归结为:
从4个不同的元素a、b、c、d中任意取出3个,并按百位、
十位、个位的顺序排成一列,共有多少种不同的排列方法?
●所有不同的排列是abc,abd,acb,acd,adb,adc;
bac,bad,bca,bed,bda,
bdc;
cab,cad,cba,
cbd,cda,
edb;
dab,
dac,
dba,
dbc,dca,
dcb.
不排列方法种数4×3×2=24
