2024年中考数学二轮复习题型突破课件:反比例函数与几何图形的综合题(共20张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:反比例函数与几何图形的综合题(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 994.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
反比例函数与几何图形的综合题
类型1 反比例函数与三角形的综合
方法指导:反比例函数图象与三角形结合时,常以求与坐标轴平行的线段长度或三角形的面积呈现,能熟练地将线段的长度与图象上某些关键点的坐标相互转化是解题关键.
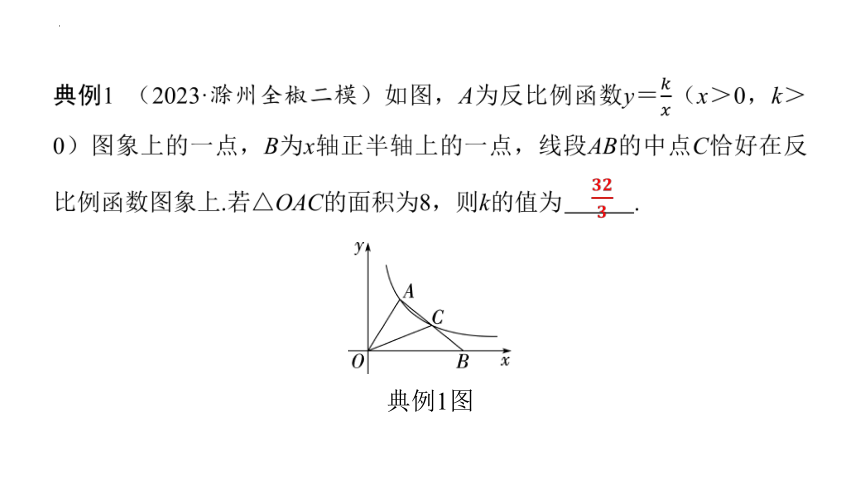
典例1图
典例1 (2023·滁州全椒二模)如图,A为反比例函数y=(x>0,k>0)图象上的一点,B为x轴正半轴上的一点,线段AB的中点C恰好在反比例函数图象上.若△OAC的面积为8,则k的值为 .
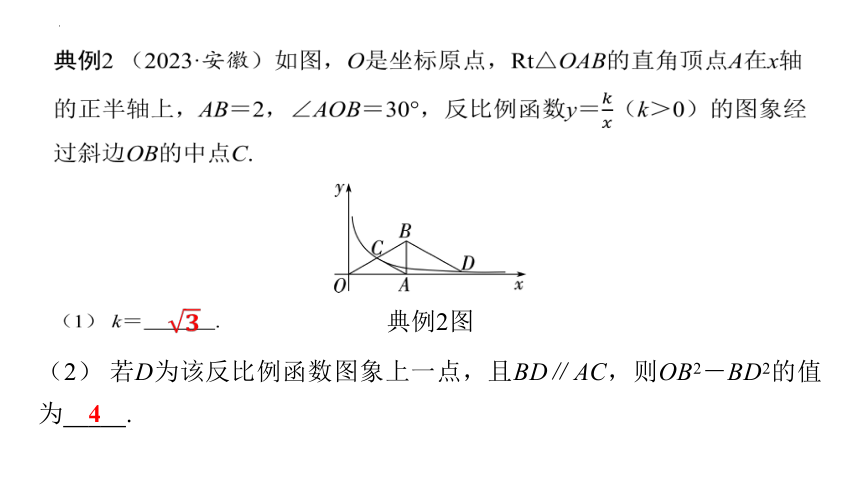
典例2 (2023·安徽)如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.
典例2图
(1) k= .
(2) 若D为该反比例函数图象上一点,且BD∥AC,则OB2-BD2的值为 4 .
4
类型2 反比例函数与四边形的综合
方法指导:反比例函数图象与四边形结合时,四边形常以特殊四边形的形态出现,如平行四边形、矩形、菱形、梯形等.确定反比例函数中的比例系数k的值时,往往需要一个独立条件,结合图形特征从面积、平行于坐标轴的线段等切入解题,并始终抓住xy=k这个隐含条件.
1. 反比例函数与平行四边形的综合
典例3 (2023·池州贵池二模)如图,四边形ABCD为平行四边形,AB和CD平行于x轴,点A在函数y=-的图象上,点B,D在函数y=的图象上,点C在y轴上,则四边形ABCD的面积为( C )
典例3图
C
A. 13 B. 18 C. 21 D. 26
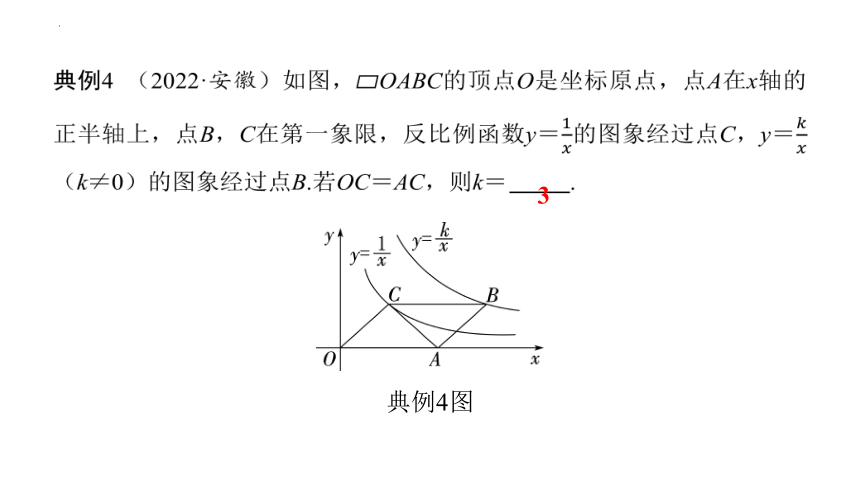
典例4 (2022·安徽)如图, OABC的顶点O是坐标原点,点A在x轴的正半轴上,点B,C在第一象限,反比例函数y=的图象经过点C,y=(k≠0)的图象经过点B.若OC=AC,则k= 3 .
典例4图
3
2. 反比例函数与矩形的综合
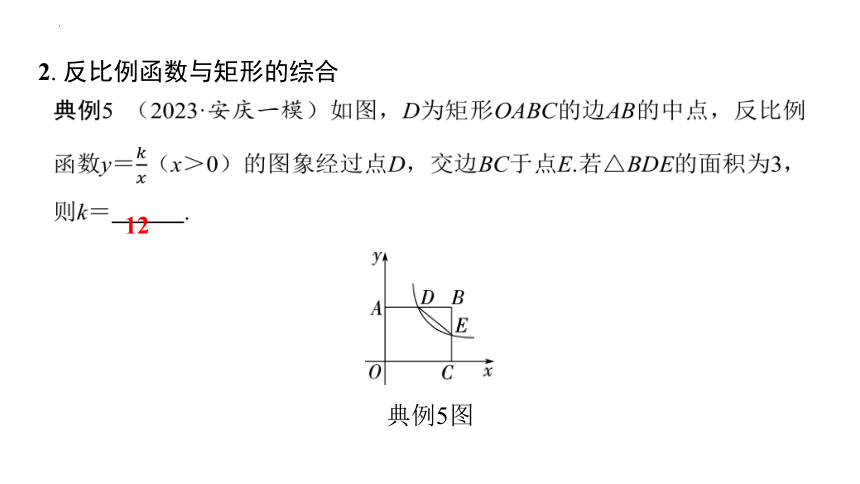
典例5 (2023·安庆一模)如图,D为矩形OABC的边AB的中点,反比例函数y=(x>0)的图象经过点D,交边BC于点E.若△BDE的面积为3,则k= 12 .
典例5图
12
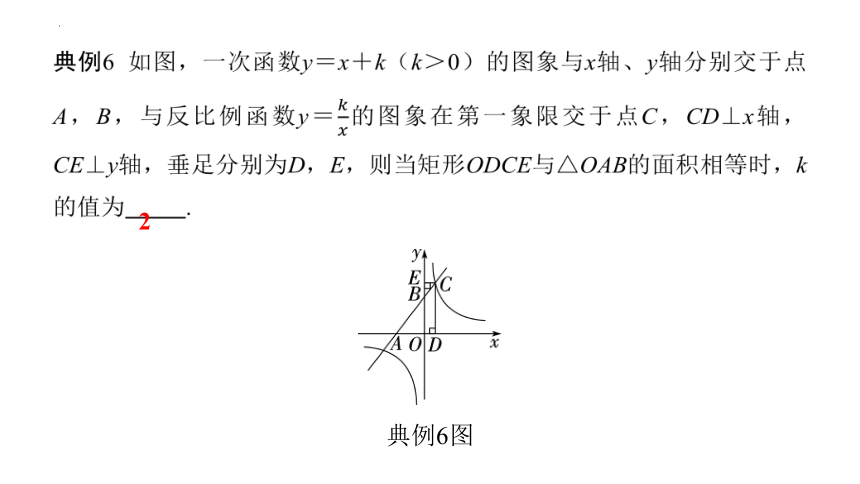
典例6 如图,一次函数y=x+k(k>0)的图象与x轴、y轴分别交于点A,B,与反比例函数y=的图象在第一象限交于点C,CD⊥x轴,CE⊥y轴,垂足分别为D,E,则当矩形ODCE与△OAB的面积相等时,k的值为 2 .
典例6图
2
3. 反比例函数与菱形的综合
典例7 (2023·合肥包河二模)如图,菱形ABCD的顶点B在y轴的正半轴上,顶点C在x轴的正半轴上,顶点A,D在第一象限,且BD∥x轴,E为对角线AC,BD的交点,OE的延长线交AD于点F,反比例函数y=(k≠0)的图象经过点F.若菱形ABCD的面积为16,则k的值为 18 .
典例7图
18
典例8 (2023·宿州砀山一模)如图,菱形OABC的顶点O是原点,顶点B在y轴上,反比例函数y=(x>0)的图象经过顶点A.若菱形OABC的面积为16,则k的值为 8 .
典例8图
8
4. 反比例函数与正方形的综合
典例9 (2023·亳州利辛模拟)如图,正方形ABCD的顶点A,D分别在函数y=-(x<0)和y=(x>0)的图象上,点B,C在x轴上,则点D的坐标为( B )
典例9图
B
A. (1,3) B. (2,3)
C. (2,2) D. (3,2)
5. 反比例函数与梯形的综合
典例10 (2023·滁州二模)如图,点A,B在函数y=(x>0)的图象上,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接OA,AB.若OD=CD,且四边形OABC的面积为15,求k的值.
典例10图
解:设点A,则OD=a,AD=.∵ OD=CD,∴ OC=2a.∴ 点B.∴ BC=.∵ 四边形OABC的面积为15,∴ S△AOD+S梯形ABCD=15.∴ a·+(+)·a=15.∴ +=15,解得k=12.
强化练习
1. (2023·湘潭)如图,A是反比例函数y=(k≠0)图象上的一点,过点A分别作AM⊥x 轴于点M,AN⊥y轴于点N.若四边形AMON的面积为2,则k的值为( A )
A. 2 B. -2 C. 1 D. -1
第1题
A
1
2
3
4
5
2. (2023·福建)如图,正方形的四个顶点分别位于反比例函数y=和y=的图象的四个分支上,则n的值为( A )
A. -3 B. - C. D. 3
第2题
A
1
2
3
4
5
3. (2023·威海)如图,点A,B在反比例函数y=(x>0)的图象上,点A的坐标为(m,2),连接OA,OB,AB.若OA=AB,∠OAB=90°,则k的值为 2-2 .
第3题
2-2
1
2
3
4
5
4. (2023·池州模拟)如图,点A,B分别在反比例函数y=-(x<0)和y=(x>0)的图象上,以OA,OB为邻边作 AOBC,点C恰好落在y轴上,且边BC交函数y=(x>0)的图象于点D,当BD=2CD时,k= 4 .
4
第4题
1
2
3
4
5
5. (2023·乐山)如图,一次函数y=kx+b与反比例函数y=的图象交于点A(m,4),与x轴交于点B,与y轴交于点C(0,3),连接OA.
(1) 求m的值和一次函数的表达式.
解:(1) ∵ 点A(m,4)在反比例函数 y= 的图象上,∴ 4=.∴ m=1.∴ 点A(1,4).又∵ 点A(1,4),C(0,3)都在一次函数y=kx+b的图象上,∴ 解得∴ 一次函数的表达式为y=x+3
1
2
3
4
5
(2) 已知P为反比例函数y=的图象上一点,=2,求点P的坐标.
解:(2) 在y=x+3中,令y=0,得x=-3,
∴ OB=3.如图,过点A作 AH⊥y 轴于点H,过点P作 PD⊥x 轴于点D,连接BP,OP.∵ 点A(1,4),C(0,3),∴ AH=1,OC=3.∵ S△OBP=2S△OAC,∴ OB·PD=2×OC·AH,即×3×PD=2××3×1,解得PD=2.∴ 点P的纵坐标为2或-2.将y=2或y=-2代入y=,得x=2或x=-2.
∴ 点P的坐标为(2,2)或(-2,-2)
第5题答案
1
2
3
4
5
反比例函数与几何图形的综合题
类型1 反比例函数与三角形的综合
方法指导:反比例函数图象与三角形结合时,常以求与坐标轴平行的线段长度或三角形的面积呈现,能熟练地将线段的长度与图象上某些关键点的坐标相互转化是解题关键.
典例1图
典例1 (2023·滁州全椒二模)如图,A为反比例函数y=(x>0,k>0)图象上的一点,B为x轴正半轴上的一点,线段AB的中点C恰好在反比例函数图象上.若△OAC的面积为8,则k的值为 .
典例2 (2023·安徽)如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.
典例2图
(1) k= .
(2) 若D为该反比例函数图象上一点,且BD∥AC,则OB2-BD2的值为 4 .
4
类型2 反比例函数与四边形的综合
方法指导:反比例函数图象与四边形结合时,四边形常以特殊四边形的形态出现,如平行四边形、矩形、菱形、梯形等.确定反比例函数中的比例系数k的值时,往往需要一个独立条件,结合图形特征从面积、平行于坐标轴的线段等切入解题,并始终抓住xy=k这个隐含条件.
1. 反比例函数与平行四边形的综合
典例3 (2023·池州贵池二模)如图,四边形ABCD为平行四边形,AB和CD平行于x轴,点A在函数y=-的图象上,点B,D在函数y=的图象上,点C在y轴上,则四边形ABCD的面积为( C )
典例3图
C
A. 13 B. 18 C. 21 D. 26
典例4 (2022·安徽)如图, OABC的顶点O是坐标原点,点A在x轴的正半轴上,点B,C在第一象限,反比例函数y=的图象经过点C,y=(k≠0)的图象经过点B.若OC=AC,则k= 3 .
典例4图
3
2. 反比例函数与矩形的综合
典例5 (2023·安庆一模)如图,D为矩形OABC的边AB的中点,反比例函数y=(x>0)的图象经过点D,交边BC于点E.若△BDE的面积为3,则k= 12 .
典例5图
12
典例6 如图,一次函数y=x+k(k>0)的图象与x轴、y轴分别交于点A,B,与反比例函数y=的图象在第一象限交于点C,CD⊥x轴,CE⊥y轴,垂足分别为D,E,则当矩形ODCE与△OAB的面积相等时,k的值为 2 .
典例6图
2
3. 反比例函数与菱形的综合
典例7 (2023·合肥包河二模)如图,菱形ABCD的顶点B在y轴的正半轴上,顶点C在x轴的正半轴上,顶点A,D在第一象限,且BD∥x轴,E为对角线AC,BD的交点,OE的延长线交AD于点F,反比例函数y=(k≠0)的图象经过点F.若菱形ABCD的面积为16,则k的值为 18 .
典例7图
18
典例8 (2023·宿州砀山一模)如图,菱形OABC的顶点O是原点,顶点B在y轴上,反比例函数y=(x>0)的图象经过顶点A.若菱形OABC的面积为16,则k的值为 8 .
典例8图
8
4. 反比例函数与正方形的综合
典例9 (2023·亳州利辛模拟)如图,正方形ABCD的顶点A,D分别在函数y=-(x<0)和y=(x>0)的图象上,点B,C在x轴上,则点D的坐标为( B )
典例9图
B
A. (1,3) B. (2,3)
C. (2,2) D. (3,2)
5. 反比例函数与梯形的综合
典例10 (2023·滁州二模)如图,点A,B在函数y=(x>0)的图象上,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C,连接OA,AB.若OD=CD,且四边形OABC的面积为15,求k的值.
典例10图
解:设点A,则OD=a,AD=.∵ OD=CD,∴ OC=2a.∴ 点B.∴ BC=.∵ 四边形OABC的面积为15,∴ S△AOD+S梯形ABCD=15.∴ a·+(+)·a=15.∴ +=15,解得k=12.
强化练习
1. (2023·湘潭)如图,A是反比例函数y=(k≠0)图象上的一点,过点A分别作AM⊥x 轴于点M,AN⊥y轴于点N.若四边形AMON的面积为2,则k的值为( A )
A. 2 B. -2 C. 1 D. -1
第1题
A
1
2
3
4
5
2. (2023·福建)如图,正方形的四个顶点分别位于反比例函数y=和y=的图象的四个分支上,则n的值为( A )
A. -3 B. - C. D. 3
第2题
A
1
2
3
4
5
3. (2023·威海)如图,点A,B在反比例函数y=(x>0)的图象上,点A的坐标为(m,2),连接OA,OB,AB.若OA=AB,∠OAB=90°,则k的值为 2-2 .
第3题
2-2
1
2
3
4
5
4. (2023·池州模拟)如图,点A,B分别在反比例函数y=-(x<0)和y=(x>0)的图象上,以OA,OB为邻边作 AOBC,点C恰好落在y轴上,且边BC交函数y=(x>0)的图象于点D,当BD=2CD时,k= 4 .
4
第4题
1
2
3
4
5
5. (2023·乐山)如图,一次函数y=kx+b与反比例函数y=的图象交于点A(m,4),与x轴交于点B,与y轴交于点C(0,3),连接OA.
(1) 求m的值和一次函数的表达式.
解:(1) ∵ 点A(m,4)在反比例函数 y= 的图象上,∴ 4=.∴ m=1.∴ 点A(1,4).又∵ 点A(1,4),C(0,3)都在一次函数y=kx+b的图象上,∴ 解得∴ 一次函数的表达式为y=x+3
1
2
3
4
5
(2) 已知P为反比例函数y=的图象上一点,=2,求点P的坐标.
解:(2) 在y=x+3中,令y=0,得x=-3,
∴ OB=3.如图,过点A作 AH⊥y 轴于点H,过点P作 PD⊥x 轴于点D,连接BP,OP.∵ 点A(1,4),C(0,3),∴ AH=1,OC=3.∵ S△OBP=2S△OAC,∴ OB·PD=2×OC·AH,即×3×PD=2××3×1,解得PD=2.∴ 点P的纵坐标为2或-2.将y=2或y=-2代入y=,得x=2或x=-2.
∴ 点P的坐标为(2,2)或(-2,-2)
第5题答案
1
2
3
4
5
同课章节目录
