2024年中考数学二轮复习题型突破课件:构造辅助圆解题(共30张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:构造辅助圆解题(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:34:21 | ||
图片预览



文档简介
(共30张PPT)
构造辅助圆解题
类型1 定点定长构造辅助圆
模型解读:如图,若OA=OB=OC=OD,则点A,B,C,D在以点O为圆心,OA(或OB,OC,OD)为半径的圆上(本质是依据圆的定义,圆是平面内所有到定点的距离等于定长的点的集合).
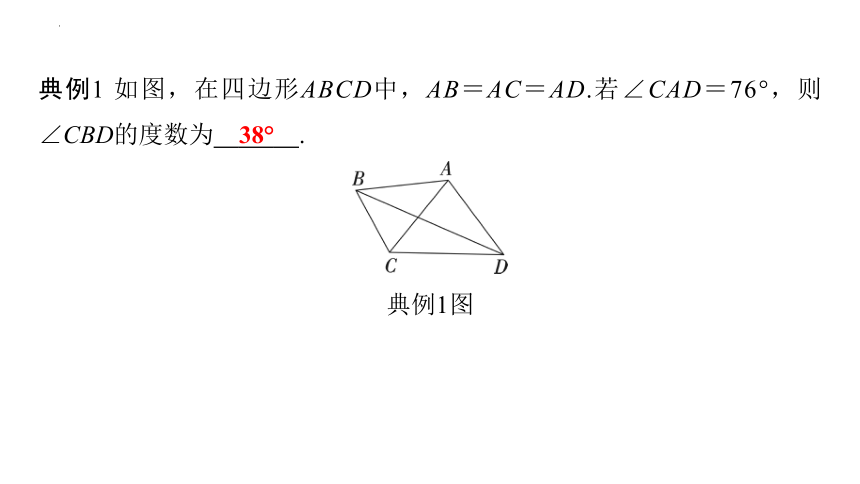
典例1 如图,在四边形ABCD中,AB=AC=AD.若∠CAD=76°,则∠CBD的度数为 38° .
典例1图
38°
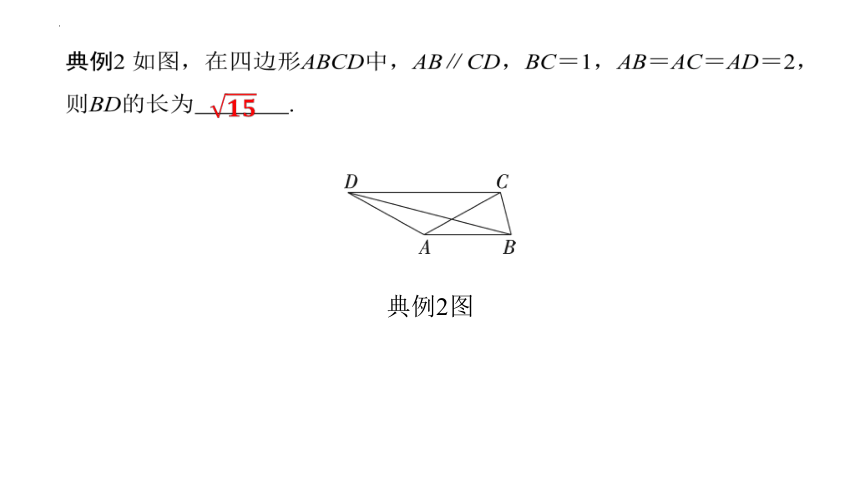
典例2图
典例2 如图,在四边形ABCD中,AB∥CD,BC=1,AB=AC=AD=2,则BD的长为 .
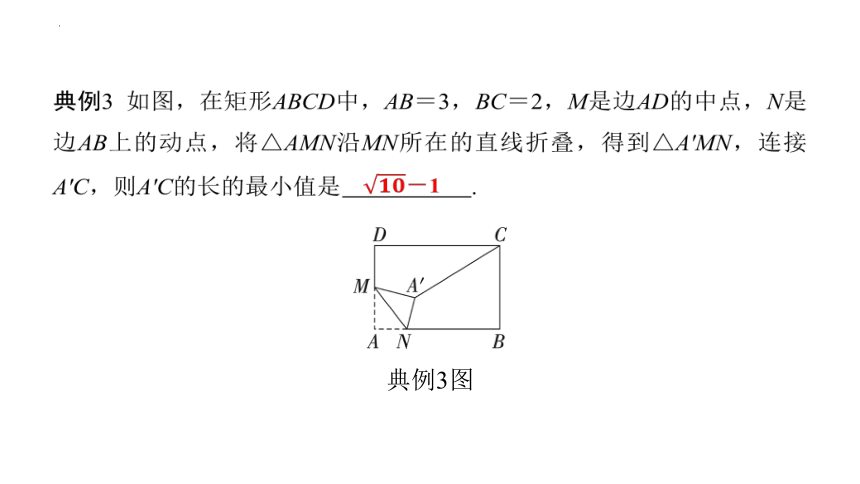
典例3 如图,在矩形ABCD中,AB=3,BC=2,M是边AD的中点,N是边AB上的动点,将△AMN沿MN所在的直线折叠,得到△A'MN,连接A'C,则A'C的长的最小值是 -1 .
典例3图
-1
类型2 利用四点构造辅助圆
模型解读:
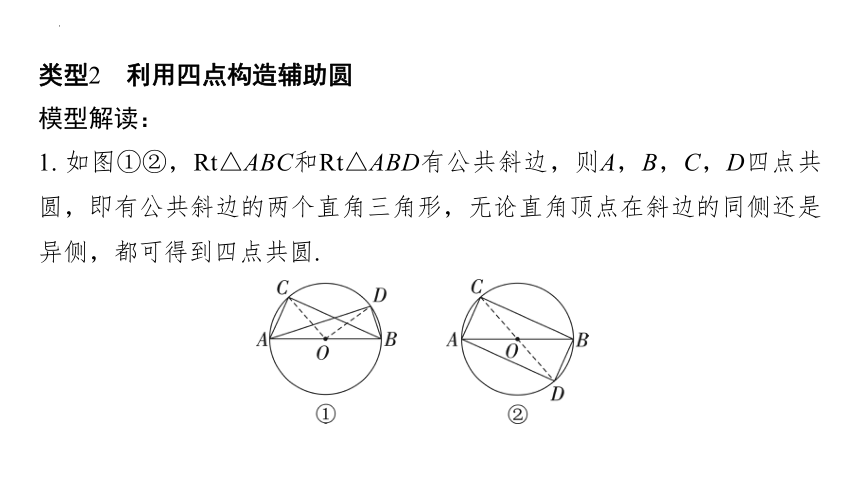
1. 如图①②,Rt△ABC和Rt△ABD有公共斜边,则A,B,C,D四点共圆,即有公共斜边的两个直角三角形,无论直角顶点在斜边的同侧还是异侧,都可得到四点共圆.
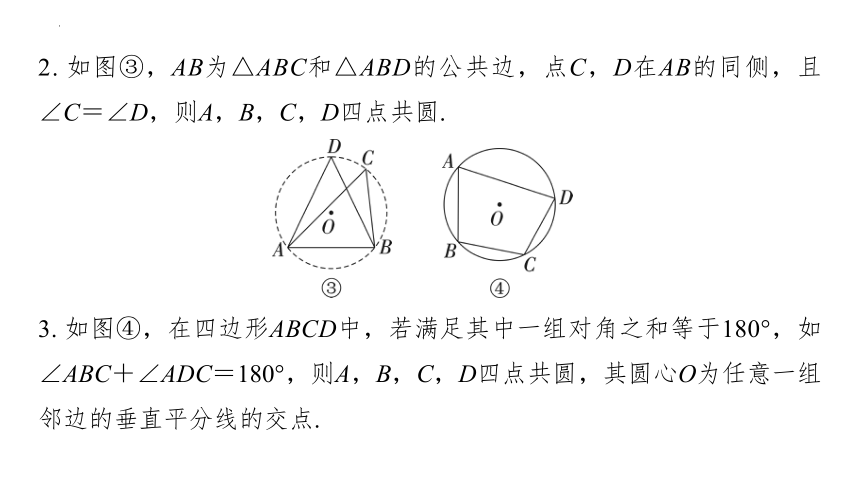
2. 如图③,AB为△ABC和△ABD的公共边,点C,D在AB的同侧,且∠C=∠D,则A,B,C,D四点共圆.
3. 如图④,在四边形ABCD中,若满足其中一组对角之和等于180°,如∠ABC+∠ADC=180°,则A,B,C,D四点共圆,其圆心O为任意一组邻边的垂直平分线的交点.
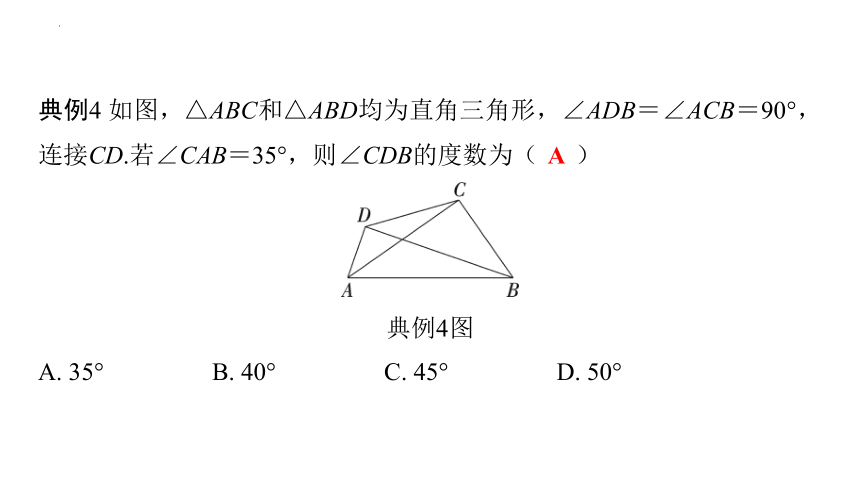
典例4 如图,△ABC和△ABD均为直角三角形,∠ADB=∠ACB=90°,连接CD.若∠CAB=35°,则∠CDB的度数为( A )
典例4图
A. 35° B. 40° C. 45° D. 50°
A
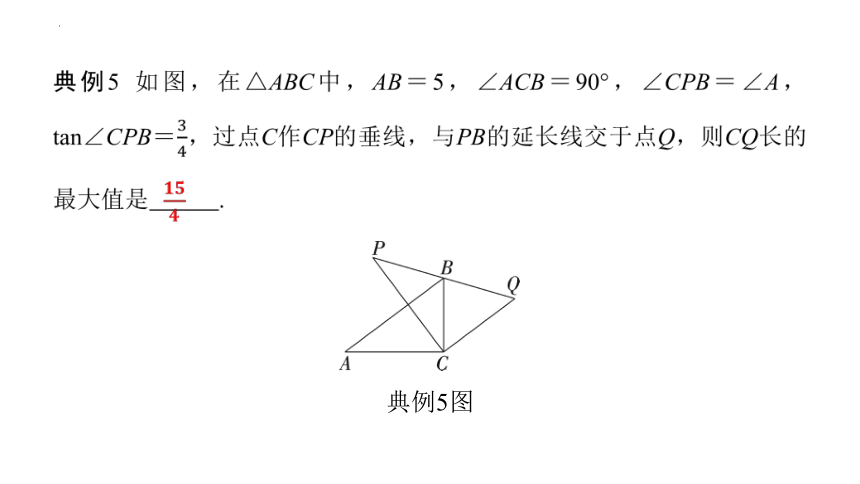
典例5 如图,在△ABC中,AB=5,∠ACB=90°,∠CPB=∠A,tan∠CPB=,过点C作CP的垂线,与PB的延长线交于点Q,则CQ长的最大值是 .
典例5图
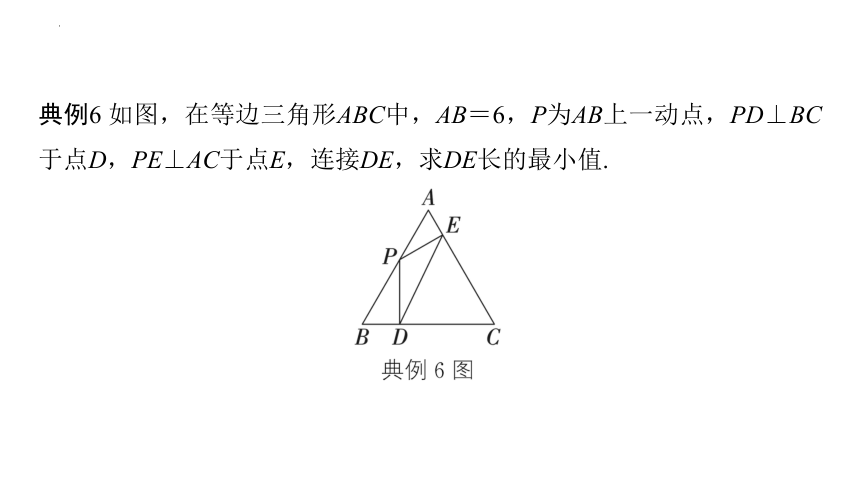
典例6 如图,在等边三角形ABC中,AB=6,P为AB上一动点,PD⊥BC于点D,PE⊥AC于点E,连接DE,求DE长的最小值.
解:如图,连接PC,取CP的中点O,连接OE,OD,过点O作OH⊥DE于点H.∵ △ABC是等边三角形,∴ ∠ACB=∠B=60°,AB=BC=AC=6.∵ PD⊥BC,PE⊥AC,∴ ∠PEC=∠PDC=90°.∵ OP=OC,
∴ OE=OP=OC=OD.∴ C,D,P,E四点在以点O为圆心,OC长为半径的圆上.∴ ∠EOD=2∠ECD=120°.∵ OH⊥DE,∴ DH=EH,∠EOH=∠DOE=60°.∴ DE=2EH=2OE·sin∠EOH=OE=CP.∴ 当CP的值最小时,DE的值最小.根据垂线段最短,可知当CP⊥AB时,CP的长取得最小值,此时CP=BC·sinB=3.∴ DE长的最小值为×3=.
典例6图答案
类型3 定弦对定角构造辅助圆
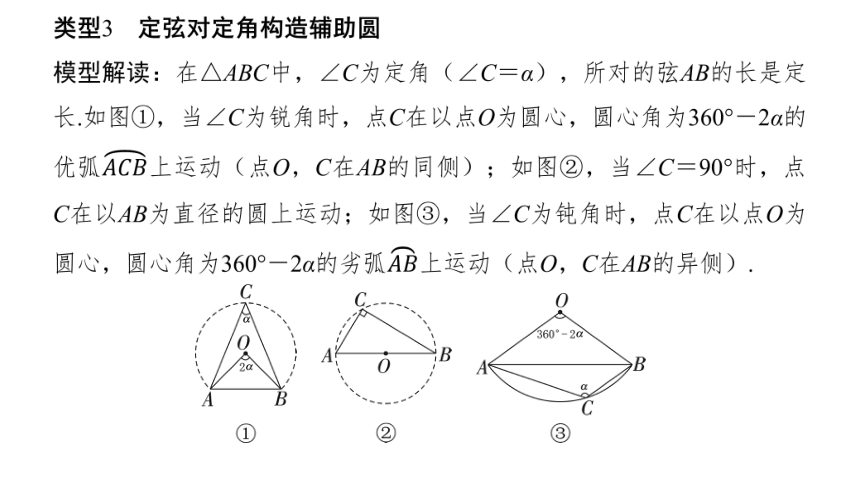
模型解读:在△ABC中,∠C为定角(∠C=α),所对的弦AB的长是定长.如图①,当∠C为锐角时,点C在以点O为圆心,圆心角为360°-2α的优弧上运动(点O,C在AB的同侧);如图②,当∠C=90°时,点C在以AB为直径的圆上运动;如图③,当∠C为钝角时,点C在以点O为圆心,圆心角为360°-2α的劣弧上运动(点O,C在AB的异侧).
典例7 如图,∠ABC=∠EAD=90°,D是线段AB上的动点且AC⊥ED于点G,AB=AE=4,则BG长的最小值为( C )
典例7图
A. 2 B. 2-1
C. 2-2 D.
C
典例8 如图,O是等边三角形ABC内一点,连接OA,OB,OC,且∠AOB=135°.若AB=2,则OC长的最小值为 1+- .
典例8图
1+-
典例9 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,求线段CE长的最小值.
解:如图,取AB的中点O,以点O为圆心,OA长为半径画半圆O.
∵ AE⊥BE,∴ 点E在半圆O上,连接CO交半圆O于点E',则当点E位于点E'的位置时,线段CE的长取得最小值.∵ AB=4,O为AB的中点,
∴ OA=OB=OE'=2.∵ 四边形ABCD是矩形,∴ ∠ABC=90°.∵ BC=6,∴ OC===2.∴ CE'=OC-OE'=2-2.
∴ 线段CE长的最小值为2-2.
典例9图答案
强化练习
1. 如图,正方形ABCD的边长为2,点E在边BC上,沿AE将正方形进行折叠,使点B落在正方形ABCD内部的点P处,则CP长的最小值是( C )
A. 2 B. 2-
C. 2-2 D. 2+2
第1题
C
1
2
3
4
5
6
7
8
9
10
11
12
2. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AB=5,D是边BC上一动点,连接AD,在AD上取一点E,使∠DAC=∠DCE,连接BE,则BE长的最小值为( C )
A. 2-3 B.
C. -2 D.
第2题
C
1
2
3
4
5
6
7
8
9
10
11
12
3. 如图,在△ABC中,BE,CD分别是边AC,AB上的高,且BC=DE,BE=6,则AE的长为( B )
A. B. 2
C. D.
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
4. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,E为边BC上的动点,将△CEF沿直线EF翻折,使点C落在点P处,则点P到边AB距离的最小值是( B )
A. 1.5 B. 1.2
C. 2.4 D. 以上都不对
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
5. (2023·亳州谯城一模)如图,在矩形ABCD中,AB=4,BC=6,P是矩形ABCD内的一点,连接PA,PC,PD.若PA⊥PD,则PC长的最小值为( C )
A. 2-4 B. 2-3
C. 2 D. 4
第5题
C
1
2
3
4
5
6
7
8
9
10
11
12
6. (2023·合肥瑶海一模)如图,在△ABC中,∠B=45°,AC=2,以AC为边作等腰直角三角形ACD,连接BD,则BD长的最大值是( D )
A. - B. +
C. 2 D. +
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
7. 如图,正方形ABCD的边长为8,E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,P是边AB上的一个动点,连接PD,PE,则PD+PE的最小值为( D )
A. 8 B. 4
C. 8-4 D. 4-4
第7题
D
1
2
3
4
5
6
7
8
9
10
11
12
8. 如图,O为线段BC的中点,点A,C,D到点O的距离相等.若∠ABC=50°,则∠ADC的度数是 130° .
第8题
130°
1
2
3
4
5
6
7
8
9
10
11
12
9. 如图,直尺的宽度为2cm,A,B两点在直尺的一条边上,AB=8cm,C,D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C,D两点之间的距离为 4 cm.
第9题
4
1
2
3
4
5
6
7
8
9
10
11
12
10. (2023·合肥模拟)如图,在矩形ABCD中,AB=6,BC=4,P是矩形内部的一个动点,且满足∠BCP=∠PDC.
第10题
(1) 线段BP的长的最小值是 2 .
(2) 当BP的长取最小值时,设DP的延长线交线段BC于点E,则CE的长为 3 .
2
3
1
2
3
4
5
6
7
8
9
10
11
12
11. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,连接PA,PB,PC,且满足∠PAB=∠PBC.
第11题
(1) ∠APB= 90° .
(2) 当线段CP最短时,△BCP的面积为 .
90°
1
2
3
4
5
6
7
8
9
10
11
12
12. 如图,四边形ABCD为矩形,BE平分∠ABC,交AD于点F,∠AEC=90°,连接AC,DE.
(1) 求∠ACE的度数.
解:(1) ∵ 四边形ABCD为矩形,∴ ∠ABC=90°.又∵ ∠AEC=90°,∴ ∠ABC+∠AEC=180°.∴ A,B,C,E四点共圆.∵ ∠ABC=90°,BE平分∠ABC,
∴ ∠ABE=45°.∴ ∠ACE=∠ABE=45°
第12题
1
2
3
4
5
6
7
8
9
10
11
12
(2) 求证:BE⊥ED.
解:(2) 连接BD.∵ 四边形ABCD是矩形,∴ A,B,C,D四点共圆,并且BD为直径.又∵ A,B,C,E四点共圆,∴ A,B,C,D,E五点共圆,且BD为直径.
∴ ∠BED=90°,即BE⊥ED
第12题
1
2
3
4
5
6
7
8
9
10
11
12
构造辅助圆解题
类型1 定点定长构造辅助圆
模型解读:如图,若OA=OB=OC=OD,则点A,B,C,D在以点O为圆心,OA(或OB,OC,OD)为半径的圆上(本质是依据圆的定义,圆是平面内所有到定点的距离等于定长的点的集合).
典例1 如图,在四边形ABCD中,AB=AC=AD.若∠CAD=76°,则∠CBD的度数为 38° .
典例1图
38°
典例2图
典例2 如图,在四边形ABCD中,AB∥CD,BC=1,AB=AC=AD=2,则BD的长为 .
典例3 如图,在矩形ABCD中,AB=3,BC=2,M是边AD的中点,N是边AB上的动点,将△AMN沿MN所在的直线折叠,得到△A'MN,连接A'C,则A'C的长的最小值是 -1 .
典例3图
-1
类型2 利用四点构造辅助圆
模型解读:
1. 如图①②,Rt△ABC和Rt△ABD有公共斜边,则A,B,C,D四点共圆,即有公共斜边的两个直角三角形,无论直角顶点在斜边的同侧还是异侧,都可得到四点共圆.
2. 如图③,AB为△ABC和△ABD的公共边,点C,D在AB的同侧,且∠C=∠D,则A,B,C,D四点共圆.
3. 如图④,在四边形ABCD中,若满足其中一组对角之和等于180°,如∠ABC+∠ADC=180°,则A,B,C,D四点共圆,其圆心O为任意一组邻边的垂直平分线的交点.
典例4 如图,△ABC和△ABD均为直角三角形,∠ADB=∠ACB=90°,连接CD.若∠CAB=35°,则∠CDB的度数为( A )
典例4图
A. 35° B. 40° C. 45° D. 50°
A
典例5 如图,在△ABC中,AB=5,∠ACB=90°,∠CPB=∠A,tan∠CPB=,过点C作CP的垂线,与PB的延长线交于点Q,则CQ长的最大值是 .
典例5图
典例6 如图,在等边三角形ABC中,AB=6,P为AB上一动点,PD⊥BC于点D,PE⊥AC于点E,连接DE,求DE长的最小值.
解:如图,连接PC,取CP的中点O,连接OE,OD,过点O作OH⊥DE于点H.∵ △ABC是等边三角形,∴ ∠ACB=∠B=60°,AB=BC=AC=6.∵ PD⊥BC,PE⊥AC,∴ ∠PEC=∠PDC=90°.∵ OP=OC,
∴ OE=OP=OC=OD.∴ C,D,P,E四点在以点O为圆心,OC长为半径的圆上.∴ ∠EOD=2∠ECD=120°.∵ OH⊥DE,∴ DH=EH,∠EOH=∠DOE=60°.∴ DE=2EH=2OE·sin∠EOH=OE=CP.∴ 当CP的值最小时,DE的值最小.根据垂线段最短,可知当CP⊥AB时,CP的长取得最小值,此时CP=BC·sinB=3.∴ DE长的最小值为×3=.
典例6图答案
类型3 定弦对定角构造辅助圆
模型解读:在△ABC中,∠C为定角(∠C=α),所对的弦AB的长是定长.如图①,当∠C为锐角时,点C在以点O为圆心,圆心角为360°-2α的优弧上运动(点O,C在AB的同侧);如图②,当∠C=90°时,点C在以AB为直径的圆上运动;如图③,当∠C为钝角时,点C在以点O为圆心,圆心角为360°-2α的劣弧上运动(点O,C在AB的异侧).
典例7 如图,∠ABC=∠EAD=90°,D是线段AB上的动点且AC⊥ED于点G,AB=AE=4,则BG长的最小值为( C )
典例7图
A. 2 B. 2-1
C. 2-2 D.
C
典例8 如图,O是等边三角形ABC内一点,连接OA,OB,OC,且∠AOB=135°.若AB=2,则OC长的最小值为 1+- .
典例8图
1+-
典例9 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,求线段CE长的最小值.
解:如图,取AB的中点O,以点O为圆心,OA长为半径画半圆O.
∵ AE⊥BE,∴ 点E在半圆O上,连接CO交半圆O于点E',则当点E位于点E'的位置时,线段CE的长取得最小值.∵ AB=4,O为AB的中点,
∴ OA=OB=OE'=2.∵ 四边形ABCD是矩形,∴ ∠ABC=90°.∵ BC=6,∴ OC===2.∴ CE'=OC-OE'=2-2.
∴ 线段CE长的最小值为2-2.
典例9图答案
强化练习
1. 如图,正方形ABCD的边长为2,点E在边BC上,沿AE将正方形进行折叠,使点B落在正方形ABCD内部的点P处,则CP长的最小值是( C )
A. 2 B. 2-
C. 2-2 D. 2+2
第1题
C
1
2
3
4
5
6
7
8
9
10
11
12
2. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AB=5,D是边BC上一动点,连接AD,在AD上取一点E,使∠DAC=∠DCE,连接BE,则BE长的最小值为( C )
A. 2-3 B.
C. -2 D.
第2题
C
1
2
3
4
5
6
7
8
9
10
11
12
3. 如图,在△ABC中,BE,CD分别是边AC,AB上的高,且BC=DE,BE=6,则AE的长为( B )
A. B. 2
C. D.
第3题
B
1
2
3
4
5
6
7
8
9
10
11
12
4. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,E为边BC上的动点,将△CEF沿直线EF翻折,使点C落在点P处,则点P到边AB距离的最小值是( B )
A. 1.5 B. 1.2
C. 2.4 D. 以上都不对
第4题
B
1
2
3
4
5
6
7
8
9
10
11
12
5. (2023·亳州谯城一模)如图,在矩形ABCD中,AB=4,BC=6,P是矩形ABCD内的一点,连接PA,PC,PD.若PA⊥PD,则PC长的最小值为( C )
A. 2-4 B. 2-3
C. 2 D. 4
第5题
C
1
2
3
4
5
6
7
8
9
10
11
12
6. (2023·合肥瑶海一模)如图,在△ABC中,∠B=45°,AC=2,以AC为边作等腰直角三角形ACD,连接BD,则BD长的最大值是( D )
A. - B. +
C. 2 D. +
第6题
D
1
2
3
4
5
6
7
8
9
10
11
12
7. 如图,正方形ABCD的边长为8,E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,P是边AB上的一个动点,连接PD,PE,则PD+PE的最小值为( D )
A. 8 B. 4
C. 8-4 D. 4-4
第7题
D
1
2
3
4
5
6
7
8
9
10
11
12
8. 如图,O为线段BC的中点,点A,C,D到点O的距离相等.若∠ABC=50°,则∠ADC的度数是 130° .
第8题
130°
1
2
3
4
5
6
7
8
9
10
11
12
9. 如图,直尺的宽度为2cm,A,B两点在直尺的一条边上,AB=8cm,C,D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C,D两点之间的距离为 4 cm.
第9题
4
1
2
3
4
5
6
7
8
9
10
11
12
10. (2023·合肥模拟)如图,在矩形ABCD中,AB=6,BC=4,P是矩形内部的一个动点,且满足∠BCP=∠PDC.
第10题
(1) 线段BP的长的最小值是 2 .
(2) 当BP的长取最小值时,设DP的延长线交线段BC于点E,则CE的长为 3 .
2
3
1
2
3
4
5
6
7
8
9
10
11
12
11. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,连接PA,PB,PC,且满足∠PAB=∠PBC.
第11题
(1) ∠APB= 90° .
(2) 当线段CP最短时,△BCP的面积为 .
90°
1
2
3
4
5
6
7
8
9
10
11
12
12. 如图,四边形ABCD为矩形,BE平分∠ABC,交AD于点F,∠AEC=90°,连接AC,DE.
(1) 求∠ACE的度数.
解:(1) ∵ 四边形ABCD为矩形,∴ ∠ABC=90°.又∵ ∠AEC=90°,∴ ∠ABC+∠AEC=180°.∴ A,B,C,E四点共圆.∵ ∠ABC=90°,BE平分∠ABC,
∴ ∠ABE=45°.∴ ∠ACE=∠ABE=45°
第12题
1
2
3
4
5
6
7
8
9
10
11
12
(2) 求证:BE⊥ED.
解:(2) 连接BD.∵ 四边形ABCD是矩形,∴ A,B,C,D四点共圆,并且BD为直径.又∵ A,B,C,E四点共圆,∴ A,B,C,D,E五点共圆,且BD为直径.
∴ ∠BED=90°,即BE⊥ED
第12题
1
2
3
4
5
6
7
8
9
10
11
12
同课章节目录
