2024年中考数学二轮复习题型突破课件:两个特殊四边形的综合题(共25张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:两个特殊四边形的综合题(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 718.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:37:28 | ||
图片预览






文档简介
(共25张PPT)
两个特殊四边形的综合题
类型1 已知一个特殊四边形,判断另一个四边形为特殊四边形的证明题
方法指导:解答此类题,一般应根据已知特殊四边形的性质得出边或角的关系,再结合相关数学知识,将其转化为能够使结论成立的边或角的条件,进而推理判断,得出结论.
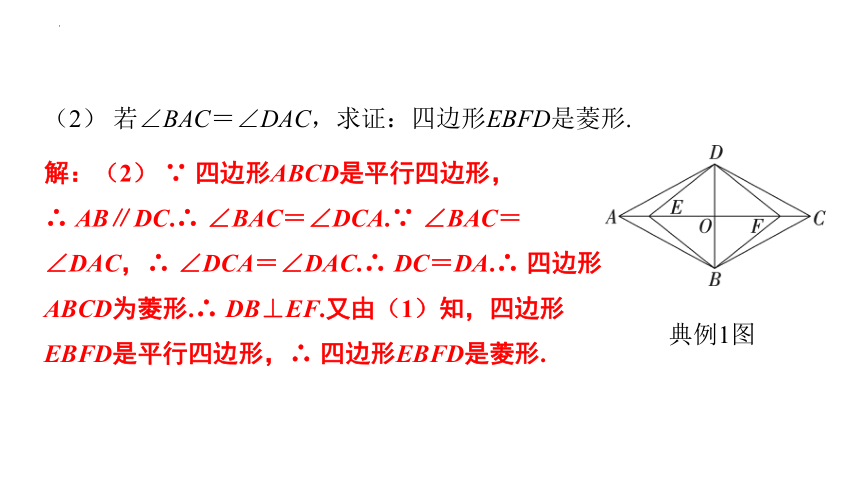
典例1 (2023·黄山黟县模拟)如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
典例1图
(1) 求证:四边形EBFD是平行四边形.
解:(1) ∵ 四边形ABCD是平行四边形,∴ OA=OC,OB=OD.∵ AE=CF,∴ OA-AE=OC-CF,即OE=OF.∴ 四边形EBFD是平行四边形.
(2) 若∠BAC=∠DAC,求证:四边形EBFD是菱形.
解:(2) ∵ 四边形ABCD是平行四边形,
∴ AB∥DC.∴ ∠BAC=∠DCA.∵ ∠BAC=∠DAC,∴ ∠DCA=∠DAC.∴ DC=DA.∴ 四边形ABCD为菱形.∴ DB⊥EF.又由(1)知,四边形EBFD是平行四边形,∴ 四边形EBFD是菱形.
典例1图
典例2 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AD的中点,连接OE,过点D作DF∥AC,交OE的延长线于点F,连接AF.
典例2图
(1) 求证:△AOE≌△DFE.
解:(1) ∵ E是AD的中点,∴ AE=DE.∵ DF∥AC,
∴ ∠OAE=∠FDE.又∵ ∠AEO=∠DEF,
∴ △AOE≌△DFE.
(2) 判断四边形AODF的形状,并说明理由.
解:(2) 四边形AODF为矩形.理由:
∵ △AOE≌△DFE,∴ AO=DF.又∵ DF∥AC,∴ 四边形AODF为平行四边形.∵ 四边形ABCD为菱形,
∴ AC⊥BD.∴ ∠AOD=90°.∴ 四边形AODF为矩形.
典例2图
类型2 已知一个特殊四边形,解题过程中需要证明另一个四边形为特殊四边形的综合题
方法指导:此类题往往并未指明要求证某个四边形为特殊四边形,但必须先证明某个四边形为特殊四边形才能达到解题目的,即隐含了要先证明某个四边形是特殊四边形的过程.解题时应善于分析,探究发现某个四边形是特殊四边形,从而找到解题途径.
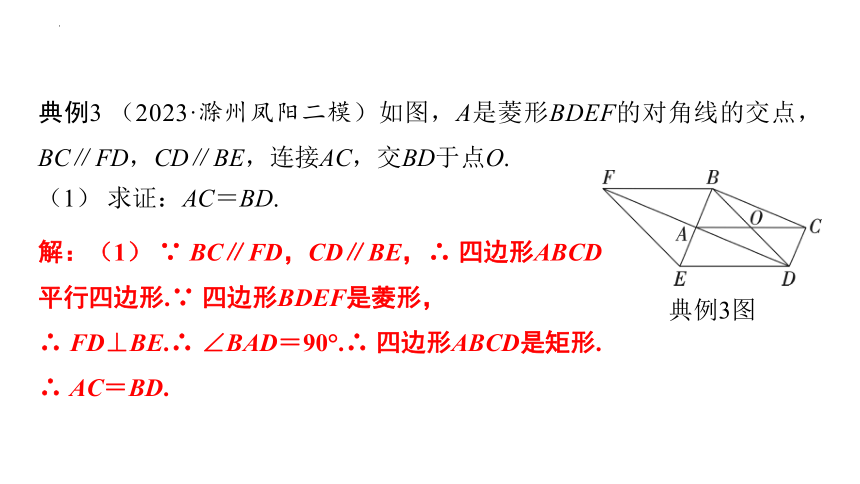
典例3 (2023·滁州凤阳二模)如图,A是菱形BDEF的对角线的交点,BC∥FD,CD∥BE,连接AC,交BD于点O.
典例3图
(1) 求证:AC=BD.
解:(1) ∵ BC∥FD,CD∥BE,∴ 四边形ABCD是平行四边形.∵ 四边形BDEF是菱形,
∴ FD⊥BE.∴ ∠BAD=90°.∴ 四边形ABCD是矩形.
∴ AC=BD.
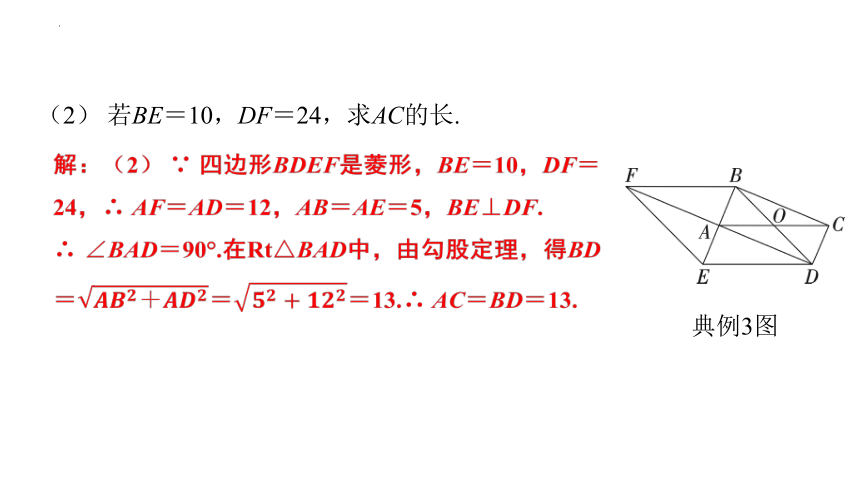
(2) 若BE=10,DF=24,求AC的长.
解:(2) ∵ 四边形BDEF是菱形,BE=10,DF=24,∴ AF=AD=12,AB=AE=5,BE⊥DF.
∴ ∠BAD=90°.在Rt△BAD中,由勾股定理,得BD===13.∴ AC=BD=13.
典例3图
典例4 如图,在 ABCD中,P为对角线AC上一动点,过点P作PM∥DC,PM=DC,连接BM,CM,BP,PD.
典例4图
(1) 求证:△ADP≌△BCM.
解:(1) ∵ PM∥DC,PM=DC,∴ 四边形CDPM是平行四边形.∴ PD=MC.∵ 四边形ABCD是平行四边形,
∴ AB∥DC,AB=DC,AD=BC.又∵ PM∥DC,PM=DC,∴ AB∥PM,AB=PM.∴ 四边形ABMP是平行四边形.
∴ AP=BM.∴ △ADP≌△BCM.
典例4图
(2) 若PA=PC,设△ABP的面积为S,四边形BMCP的面积为T,求的值.
解:(2) ∵ 由(1)知,△ADP≌△BCM,∴ S△ADP=S△BCM.∴ S四边形BMCP=S△BCM+S△BCP=S△ADP+S△BCP=S ABCD.∵ PA=PC,∴ S△ABP=S△ABC=S ABCD.∴ S=S ABCD,T=S ABCD.∴ 的值为=.
类型3 已知两个特殊四边形的综合题
方法指导:此类题综合性较强,一般应先将两个已知特殊四边形的性质挖掘出来,转化为能够计算或证明问题的边或角的条件,进而推理计算,得出问题的结论.
典例5 如图,在 ABCD中,G,H分别是AD,BC的中点,AE⊥BD,CF⊥BD,四边形GEHF是矩形.若AB=5,AD=8,则BD的长为( A )
典例5图
A
A. B. C. 8 D.
[思路点拨] 连接GH,先证四边形GABH是平行四边形,由平行四边形和矩形的性质求出EF的长,进而由△EFH∽△CBF求出BF的长;再证△ABE≌△CDF,可得BE=DF.从而由BD=BF+DF可得答案.
典例6 (2023·滁州二模)如图,在 ABCD中,∠B=60°,AB=9,AD=6,E为边AB上一动点,连接ED并延长至点F,使得DF=DE,以EC,EF为邻边构造 EFGC,连接EG交DC于点O.当EG的长最小时,AE的长为( B )
典例6图
B
A. B. 1
C. 2 D. 1+
[思路点拨] 过点A作AM⊥CD,交CD于点M.先证当OE的长最小时,EG的长最小,此时OE⊥AB;再证AE=OM,将问题转化为求DO,DM的差.而DO的长可由△DOE∽△COG而求得,DM的长可在Rt△ADM中,由30°角所对的直角边等于斜边的一半而求得.
强化练习
1. 如图,P为线段AB上一点(不与点A,B重合),分别以AP,PB为边在线段AB同侧作正方形APCD,正方形PBEF.设∠CBE=α,则∠AFP的度数为( B )
A. 2α B. 90°-α
C. 45°+α D. 90°-α
第1题
B
1
2
3
4
5
6
2. 如图,四边形ABCD和四边形BEFD都是矩形,且点C恰好在EF上.若AB=1,AD=2,则为( D )
A. 1 B.
C. D.
第2题
D
1
2
3
4
5
6
3. (2023·阜阳模拟)如图,在 ABCD中,∠ABC=45°,点E,F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=1,则CF的长为( A )
A. + B. 2
C. 4 D. +
第3题
A
1
2
3
4
5
6
4. 如图,在矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A. 2 B. 3
C. 5 D. 6
第4题
C
1
2
3
4
5
6
5. 如图,在菱形ABCD中,AB=12,∠D=60°,P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 72 .
第5题
72
1
2
3
4
5
6
6. (2023·兰州)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD,AD于点F,G,连接DE.
第6题
(1) 判断四边形OCDE的形状,并说明理由.
解:(1) 四边形OCDE是菱形 理由:∵ CD∥OE,∴ ∠FDC=∠FOE.∵ CE是线段OD的垂直平分线,∴ FD=FO,ED=EO,CD=CO.在△FDC和△FOE中,
∵ ∴ △FDC≌△FOE.∴ CD=EO.又∵ ED=EO,CD=CO,∴ ED=EO=CD=CO.∴ 四边形OCDE是菱形.
1
2
3
4
5
6
(2) 当CD=4时,求EG的长.
(2) ∵ 四边形ABCD为矩形,∴ ∠BCD=∠CDA=90°,DO=CO.
∵ CE是线段OD的垂直平分线,∴ CD=CO.∴ CD=CO=DO.∴ △ODC为等边三角形.∴ DO=CD=4,∠ODC=60°.∴ DF=DO=2.在Rt△CDF中,∠CFD=90°,CD=4,DF=2,∴ 由勾股定理,得CF==2.由(1)知,四边形OCDE是菱形,∴ EF=CF=2.∵ ∠GDF=∠CDA-∠ODC=90°-60°=30°,∠DFG=90°,
∴ tan∠GDF=.∴ GF=DF·tan∠GDF=2tan30°=.∴ EG=EF-GF=2-=
1
2
3
4
5
6
两个特殊四边形的综合题
类型1 已知一个特殊四边形,判断另一个四边形为特殊四边形的证明题
方法指导:解答此类题,一般应根据已知特殊四边形的性质得出边或角的关系,再结合相关数学知识,将其转化为能够使结论成立的边或角的条件,进而推理判断,得出结论.
典例1 (2023·黄山黟县模拟)如图,在 ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
典例1图
(1) 求证:四边形EBFD是平行四边形.
解:(1) ∵ 四边形ABCD是平行四边形,∴ OA=OC,OB=OD.∵ AE=CF,∴ OA-AE=OC-CF,即OE=OF.∴ 四边形EBFD是平行四边形.
(2) 若∠BAC=∠DAC,求证:四边形EBFD是菱形.
解:(2) ∵ 四边形ABCD是平行四边形,
∴ AB∥DC.∴ ∠BAC=∠DCA.∵ ∠BAC=∠DAC,∴ ∠DCA=∠DAC.∴ DC=DA.∴ 四边形ABCD为菱形.∴ DB⊥EF.又由(1)知,四边形EBFD是平行四边形,∴ 四边形EBFD是菱形.
典例1图
典例2 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AD的中点,连接OE,过点D作DF∥AC,交OE的延长线于点F,连接AF.
典例2图
(1) 求证:△AOE≌△DFE.
解:(1) ∵ E是AD的中点,∴ AE=DE.∵ DF∥AC,
∴ ∠OAE=∠FDE.又∵ ∠AEO=∠DEF,
∴ △AOE≌△DFE.
(2) 判断四边形AODF的形状,并说明理由.
解:(2) 四边形AODF为矩形.理由:
∵ △AOE≌△DFE,∴ AO=DF.又∵ DF∥AC,∴ 四边形AODF为平行四边形.∵ 四边形ABCD为菱形,
∴ AC⊥BD.∴ ∠AOD=90°.∴ 四边形AODF为矩形.
典例2图
类型2 已知一个特殊四边形,解题过程中需要证明另一个四边形为特殊四边形的综合题
方法指导:此类题往往并未指明要求证某个四边形为特殊四边形,但必须先证明某个四边形为特殊四边形才能达到解题目的,即隐含了要先证明某个四边形是特殊四边形的过程.解题时应善于分析,探究发现某个四边形是特殊四边形,从而找到解题途径.
典例3 (2023·滁州凤阳二模)如图,A是菱形BDEF的对角线的交点,BC∥FD,CD∥BE,连接AC,交BD于点O.
典例3图
(1) 求证:AC=BD.
解:(1) ∵ BC∥FD,CD∥BE,∴ 四边形ABCD是平行四边形.∵ 四边形BDEF是菱形,
∴ FD⊥BE.∴ ∠BAD=90°.∴ 四边形ABCD是矩形.
∴ AC=BD.
(2) 若BE=10,DF=24,求AC的长.
解:(2) ∵ 四边形BDEF是菱形,BE=10,DF=24,∴ AF=AD=12,AB=AE=5,BE⊥DF.
∴ ∠BAD=90°.在Rt△BAD中,由勾股定理,得BD===13.∴ AC=BD=13.
典例3图
典例4 如图,在 ABCD中,P为对角线AC上一动点,过点P作PM∥DC,PM=DC,连接BM,CM,BP,PD.
典例4图
(1) 求证:△ADP≌△BCM.
解:(1) ∵ PM∥DC,PM=DC,∴ 四边形CDPM是平行四边形.∴ PD=MC.∵ 四边形ABCD是平行四边形,
∴ AB∥DC,AB=DC,AD=BC.又∵ PM∥DC,PM=DC,∴ AB∥PM,AB=PM.∴ 四边形ABMP是平行四边形.
∴ AP=BM.∴ △ADP≌△BCM.
典例4图
(2) 若PA=PC,设△ABP的面积为S,四边形BMCP的面积为T,求的值.
解:(2) ∵ 由(1)知,△ADP≌△BCM,∴ S△ADP=S△BCM.∴ S四边形BMCP=S△BCM+S△BCP=S△ADP+S△BCP=S ABCD.∵ PA=PC,∴ S△ABP=S△ABC=S ABCD.∴ S=S ABCD,T=S ABCD.∴ 的值为=.
类型3 已知两个特殊四边形的综合题
方法指导:此类题综合性较强,一般应先将两个已知特殊四边形的性质挖掘出来,转化为能够计算或证明问题的边或角的条件,进而推理计算,得出问题的结论.
典例5 如图,在 ABCD中,G,H分别是AD,BC的中点,AE⊥BD,CF⊥BD,四边形GEHF是矩形.若AB=5,AD=8,则BD的长为( A )
典例5图
A
A. B. C. 8 D.
[思路点拨] 连接GH,先证四边形GABH是平行四边形,由平行四边形和矩形的性质求出EF的长,进而由△EFH∽△CBF求出BF的长;再证△ABE≌△CDF,可得BE=DF.从而由BD=BF+DF可得答案.
典例6 (2023·滁州二模)如图,在 ABCD中,∠B=60°,AB=9,AD=6,E为边AB上一动点,连接ED并延长至点F,使得DF=DE,以EC,EF为邻边构造 EFGC,连接EG交DC于点O.当EG的长最小时,AE的长为( B )
典例6图
B
A. B. 1
C. 2 D. 1+
[思路点拨] 过点A作AM⊥CD,交CD于点M.先证当OE的长最小时,EG的长最小,此时OE⊥AB;再证AE=OM,将问题转化为求DO,DM的差.而DO的长可由△DOE∽△COG而求得,DM的长可在Rt△ADM中,由30°角所对的直角边等于斜边的一半而求得.
强化练习
1. 如图,P为线段AB上一点(不与点A,B重合),分别以AP,PB为边在线段AB同侧作正方形APCD,正方形PBEF.设∠CBE=α,则∠AFP的度数为( B )
A. 2α B. 90°-α
C. 45°+α D. 90°-α
第1题
B
1
2
3
4
5
6
2. 如图,四边形ABCD和四边形BEFD都是矩形,且点C恰好在EF上.若AB=1,AD=2,则为( D )
A. 1 B.
C. D.
第2题
D
1
2
3
4
5
6
3. (2023·阜阳模拟)如图,在 ABCD中,∠ABC=45°,点E,F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=1,则CF的长为( A )
A. + B. 2
C. 4 D. +
第3题
A
1
2
3
4
5
6
4. 如图,在矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A. 2 B. 3
C. 5 D. 6
第4题
C
1
2
3
4
5
6
5. 如图,在菱形ABCD中,AB=12,∠D=60°,P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 72 .
第5题
72
1
2
3
4
5
6
6. (2023·兰州)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD,AD于点F,G,连接DE.
第6题
(1) 判断四边形OCDE的形状,并说明理由.
解:(1) 四边形OCDE是菱形 理由:∵ CD∥OE,∴ ∠FDC=∠FOE.∵ CE是线段OD的垂直平分线,∴ FD=FO,ED=EO,CD=CO.在△FDC和△FOE中,
∵ ∴ △FDC≌△FOE.∴ CD=EO.又∵ ED=EO,CD=CO,∴ ED=EO=CD=CO.∴ 四边形OCDE是菱形.
1
2
3
4
5
6
(2) 当CD=4时,求EG的长.
(2) ∵ 四边形ABCD为矩形,∴ ∠BCD=∠CDA=90°,DO=CO.
∵ CE是线段OD的垂直平分线,∴ CD=CO.∴ CD=CO=DO.∴ △ODC为等边三角形.∴ DO=CD=4,∠ODC=60°.∴ DF=DO=2.在Rt△CDF中,∠CFD=90°,CD=4,DF=2,∴ 由勾股定理,得CF==2.由(1)知,四边形OCDE是菱形,∴ EF=CF=2.∵ ∠GDF=∠CDA-∠ODC=90°-60°=30°,∠DFG=90°,
∴ tan∠GDF=.∴ GF=DF·tan∠GDF=2tan30°=.∴ EG=EF-GF=2-=
1
2
3
4
5
6
同课章节目录
