2024年中考数学二轮复习题型突破课件:与角平分线有关的辅助线问题(共24张PPT)
文档属性
| 名称 | 2024年中考数学二轮复习题型突破课件:与角平分线有关的辅助线问题(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 20:38:09 | ||
图片预览





文档简介
(共24张PPT)
与角平分线有关的辅助线问题
类型1 作垂线
模型解读:如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PA=PB,△OAP≌△OBP.
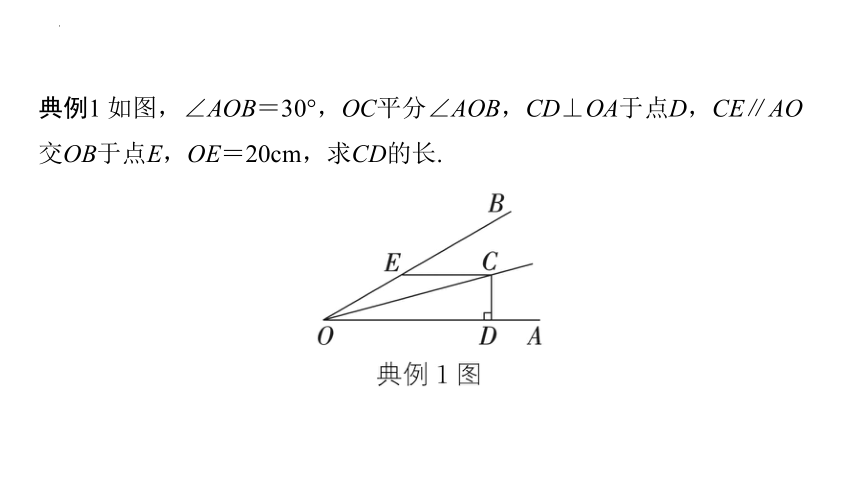
典例1 如图,∠AOB=30°,OC平分∠AOB,CD⊥OA于点D,CE∥AO交OB于点E,OE=20cm,求CD的长.
解:如图,过点C作CF⊥OB,垂足为F.∵ OC平分∠AOB,CD⊥OA,∴ ∠EOC=∠AOC=15°,CF=CD.∵ CE∥AO,∴ ∠ECO=∠AOC=15°.∴ ∠ECO=∠EOC.∴ OE=CE=20cm.∵ ∠FEC=∠EOC+∠ECO=30°,∴ CF=CE=×20=10(cm).∴ CD=10cm.
典例1图答案
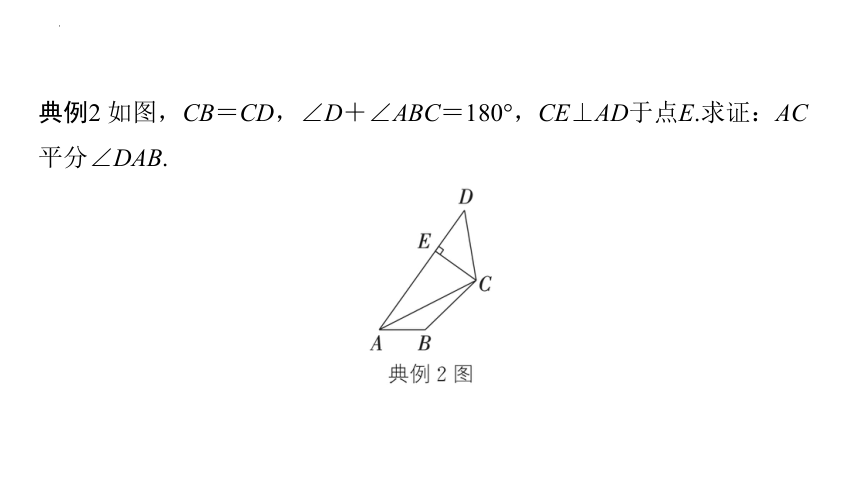
典例2 如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于点E.求证:AC平分∠DAB.
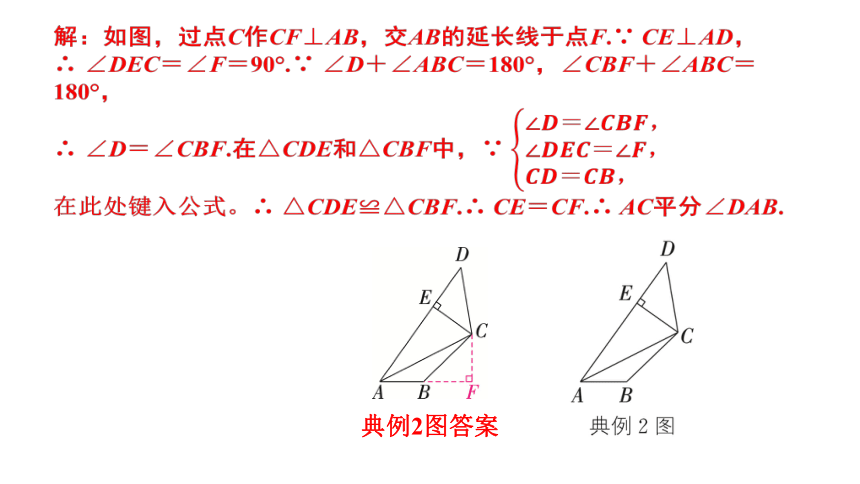
解:如图,过点C作CF⊥AB,交AB的延长线于点F.∵ CE⊥AD,
∴ ∠DEC=∠F=90°.∵ ∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴ ∠D=∠CBF.在△CDE和△CBF中,∵
∴ △CDE≌△CBF.∴ CE=CF.∴ AC平分∠DAB.
典例2图答案
类型2 作平行线
模型解读:如图,P是∠AOB的平分线上一点,过点P作PQ∥OB,交OA于点Q,则OQ=PQ,△POQ为等腰三角形.
典例3图
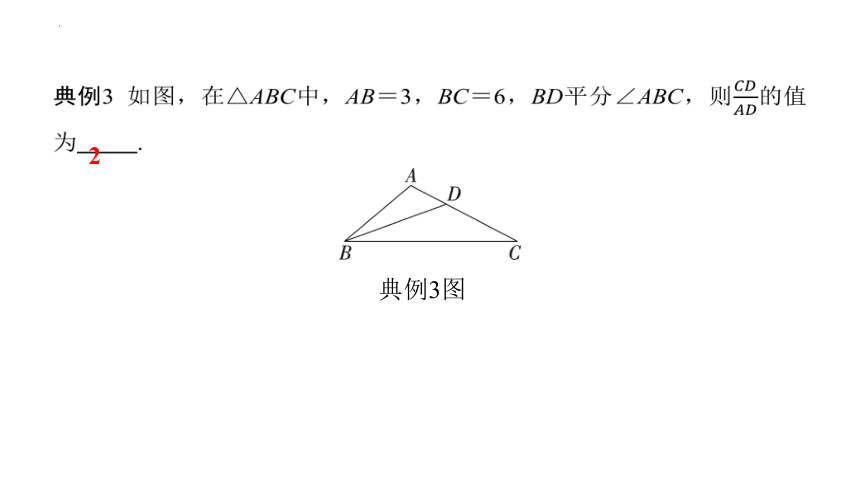
典例3 如图,在△ABC中,AB=3,BC=6,BD平分∠ABC,则的值为 2 .
2
典例4 如图,在△AOB中,∠AOB=30°,OC平分∠AOB,D为OC上一点,过点D作DE⊥OA于点E.若DE=4,求OE的长.
典例4图答案
解:∵ ∠AOB=30°,OC平分∠AOB,∴ ∠AOC=∠BOC=15°.如图,过点D作DF∥OB,交OA于点F.∴ ∠FDO=∠BOC=15°.∴ ∠FDO=∠FOD=15°.∴ OF=DF,∠DFE=∠FDO+∠FOD=15°+15°=30°.∴ 在Rt△DEF中,DF=2DE=2×4=8,EF=DE=×4=4.∴ OF=8.∴ OE=OF+EF=8+4.
典例5 如图,在△ABC中,AD平分∠CAB,交BC于点E.若∠BDA=90°,E是AD的中点,AB=5,求AC的长.
解:如图,延长AC,BD交于点F,过点D作DG∥AF,交BC于点G,则∠DGE=∠ACE.∵ E是AD的中点,∴ DE=AE.在△DGE和△ACE中,∵ ∴ △DGE≌△ACE.∴ DG=AC.∵ AD平分∠CAB,∴ ∠BAD=∠FAD.∵ ∠BDA=90°,∴ ∠FDA=90°=∠BDA.又∵ AD=AD,∴ △BAD≌△FAD.∴ AB=AF=5,BD=FD.∵ DG∥AF,∴ DG是△BCF的中位线.∴ CF=2DG.∴ AF=AC+CF=3DG=3AC.∴ AC=AF=.
典例5图答案
类型3 构造轴对称图形
模型解读:如图①,P是∠MON的平分线上一点.若AP⊥OP于点P,延长AP交ON于点B,则△AOB是等腰三角形.
如图②,P是∠MON的平分线上一点,点A在边OM上.若在边ON上截取OB=OA,连接AP,BP,则△AOP≌△BOP.
典例6 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使DE=AD.求证:BC=AB+CE.
解:如图,在BC上截取BF=AB,连接DF.∵ BD是∠ABC的平分线,∠ABC=40°,∴ ∠1=∠2=20°.在△ABD 和 △FBD 中,
∵ ∴ △ABD≌△FBD.∴ DA=DF,∠A=∠BFD.∵ DE=AD,∴ DE=DF.又∵ ∠A=100°,∠ABC=40°,∴ ∠ACB=40°,∠DFC=180°-∠BFD=80°.∴ ∠FDC=60°.∵ ∠EDC=∠ADB=180°-∠1-∠A=180°-20°-100°=60°,∴ ∠EDC=∠FDC.又∵ CD=CD,∴ △DCE≌△DCF.∴ CE=CF.∴ BC=BF+CF=AB+CE,即BC=AB+CE.
典例6图答案
强化练习
1. 如图,∠AOB=150°,OP平分∠AOB,PD⊥OB于点D,PC∥OB交OA于点C.若PD=3,则OC的长为( D )
A. 3 B. 4
C. 5 D. 6
第1题
D
1
2
3
4
5
6
7
2. 如图,E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD.有下列结论:① ∠AED=90°;② ∠ADE=∠CDE;③ DE=BE;④ AD=AB+CD.其中,正确的是( A )
A. ①②④ B. ①②③
C. ②③④ D. ①③
第2题
A
1
2
3
4
5
6
7
3. 如图,OC平分∠AOB,D,F分别是OC,OB上的点,点E,G在OA上.若OF=13,OE=18,OG=10,△ODF的面积是26,则△DEG的面积是 16 .
第3题
16
1
2
3
4
5
6
7
4. 如图,∠ADE=∠BDE=15°,EF∥DB,EC⊥DB于点C.若EC=,则EF的长为 2 .
第4题
2
1
2
3
4
5
6
7
5. 如图,在△ABC中,AD是∠BAC的平分线,BE是△ABD的边AD上的中线.若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 7.5 .
第5题
7.5
1
2
3
4
5
6
7
6. 如图,D是∠EAF平分线上的一点.若∠ACD+∠ABD=180°,求证:CD=BD.
1
2
3
4
5
6
7
解:如图,过点D分别作AE,AF的垂线,交AE于点M,交AF于点N,则∠CMD=∠BND=90°.∵ AD是∠EAF的平分线,∴ DM=DN.
∵ ∠ACD+∠ABD=180°,∠ACD+∠MCD=180°,∴ ∠MCD=∠NBD.在△CDM和△BDN中,∵ ∠CMD=∠BND=90°,∠MCD=∠NBD,DM=DN,∴ △CDM≌△BDN.∴ CD=BD
第6题答案
第6题答案
1
2
3
4
5
6
7
7. 如图,在△ABC中,∠BAC=60°,∠ABC=80°,∠BAC与∠ABC的平分线AD与BE交于点F.求证:AB+BD=AE+BE.
1
2
3
4
5
6
7
解:∵ ∠BAC=60°,∠ABC=80°,∴ ∠C=180°-(∠BAC+∠ABC)=180°-(60°+80°)=40°.∵ BE是∠ABC的平分线,
∴ ∠EBC=∠ABC=40°.∴ ∠C=∠EBC.∴ BE=EC.如图,过点D作DH∥BE,交AC于点H,则∠HDC=∠EBC=40°.∴ ∠HDC=∠C.
∴ HD=HC.∴ ∠AHD=∠HDC+∠C=40°+40°=80°.∴ ∠ABD=∠AHD.∵ AD是∠BAC的平分线,∴ ∠BAD=∠HAD.在△ABD和△AHD中,∵ ∴ △ABD≌△AHD.∴ AB=AH,BD=HD.∵ HD=HC,∴ BD=HC.∴ AB+BD=AH+HC=AC.又∵ BE=EC,∴ AE+BE=AE+EC=AC.∴ AB+BD=AE+BE
第7题答案
1
2
3
4
5
6
7
与角平分线有关的辅助线问题
类型1 作垂线
模型解读:如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PA=PB,△OAP≌△OBP.
典例1 如图,∠AOB=30°,OC平分∠AOB,CD⊥OA于点D,CE∥AO交OB于点E,OE=20cm,求CD的长.
解:如图,过点C作CF⊥OB,垂足为F.∵ OC平分∠AOB,CD⊥OA,∴ ∠EOC=∠AOC=15°,CF=CD.∵ CE∥AO,∴ ∠ECO=∠AOC=15°.∴ ∠ECO=∠EOC.∴ OE=CE=20cm.∵ ∠FEC=∠EOC+∠ECO=30°,∴ CF=CE=×20=10(cm).∴ CD=10cm.
典例1图答案
典例2 如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于点E.求证:AC平分∠DAB.
解:如图,过点C作CF⊥AB,交AB的延长线于点F.∵ CE⊥AD,
∴ ∠DEC=∠F=90°.∵ ∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴ ∠D=∠CBF.在△CDE和△CBF中,∵
∴ △CDE≌△CBF.∴ CE=CF.∴ AC平分∠DAB.
典例2图答案
类型2 作平行线
模型解读:如图,P是∠AOB的平分线上一点,过点P作PQ∥OB,交OA于点Q,则OQ=PQ,△POQ为等腰三角形.
典例3图
典例3 如图,在△ABC中,AB=3,BC=6,BD平分∠ABC,则的值为 2 .
2
典例4 如图,在△AOB中,∠AOB=30°,OC平分∠AOB,D为OC上一点,过点D作DE⊥OA于点E.若DE=4,求OE的长.
典例4图答案
解:∵ ∠AOB=30°,OC平分∠AOB,∴ ∠AOC=∠BOC=15°.如图,过点D作DF∥OB,交OA于点F.∴ ∠FDO=∠BOC=15°.∴ ∠FDO=∠FOD=15°.∴ OF=DF,∠DFE=∠FDO+∠FOD=15°+15°=30°.∴ 在Rt△DEF中,DF=2DE=2×4=8,EF=DE=×4=4.∴ OF=8.∴ OE=OF+EF=8+4.
典例5 如图,在△ABC中,AD平分∠CAB,交BC于点E.若∠BDA=90°,E是AD的中点,AB=5,求AC的长.
解:如图,延长AC,BD交于点F,过点D作DG∥AF,交BC于点G,则∠DGE=∠ACE.∵ E是AD的中点,∴ DE=AE.在△DGE和△ACE中,∵ ∴ △DGE≌△ACE.∴ DG=AC.∵ AD平分∠CAB,∴ ∠BAD=∠FAD.∵ ∠BDA=90°,∴ ∠FDA=90°=∠BDA.又∵ AD=AD,∴ △BAD≌△FAD.∴ AB=AF=5,BD=FD.∵ DG∥AF,∴ DG是△BCF的中位线.∴ CF=2DG.∴ AF=AC+CF=3DG=3AC.∴ AC=AF=.
典例5图答案
类型3 构造轴对称图形
模型解读:如图①,P是∠MON的平分线上一点.若AP⊥OP于点P,延长AP交ON于点B,则△AOB是等腰三角形.
如图②,P是∠MON的平分线上一点,点A在边OM上.若在边ON上截取OB=OA,连接AP,BP,则△AOP≌△BOP.
典例6 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使DE=AD.求证:BC=AB+CE.
解:如图,在BC上截取BF=AB,连接DF.∵ BD是∠ABC的平分线,∠ABC=40°,∴ ∠1=∠2=20°.在△ABD 和 △FBD 中,
∵ ∴ △ABD≌△FBD.∴ DA=DF,∠A=∠BFD.∵ DE=AD,∴ DE=DF.又∵ ∠A=100°,∠ABC=40°,∴ ∠ACB=40°,∠DFC=180°-∠BFD=80°.∴ ∠FDC=60°.∵ ∠EDC=∠ADB=180°-∠1-∠A=180°-20°-100°=60°,∴ ∠EDC=∠FDC.又∵ CD=CD,∴ △DCE≌△DCF.∴ CE=CF.∴ BC=BF+CF=AB+CE,即BC=AB+CE.
典例6图答案
强化练习
1. 如图,∠AOB=150°,OP平分∠AOB,PD⊥OB于点D,PC∥OB交OA于点C.若PD=3,则OC的长为( D )
A. 3 B. 4
C. 5 D. 6
第1题
D
1
2
3
4
5
6
7
2. 如图,E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD.有下列结论:① ∠AED=90°;② ∠ADE=∠CDE;③ DE=BE;④ AD=AB+CD.其中,正确的是( A )
A. ①②④ B. ①②③
C. ②③④ D. ①③
第2题
A
1
2
3
4
5
6
7
3. 如图,OC平分∠AOB,D,F分别是OC,OB上的点,点E,G在OA上.若OF=13,OE=18,OG=10,△ODF的面积是26,则△DEG的面积是 16 .
第3题
16
1
2
3
4
5
6
7
4. 如图,∠ADE=∠BDE=15°,EF∥DB,EC⊥DB于点C.若EC=,则EF的长为 2 .
第4题
2
1
2
3
4
5
6
7
5. 如图,在△ABC中,AD是∠BAC的平分线,BE是△ABD的边AD上的中线.若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是 7.5 .
第5题
7.5
1
2
3
4
5
6
7
6. 如图,D是∠EAF平分线上的一点.若∠ACD+∠ABD=180°,求证:CD=BD.
1
2
3
4
5
6
7
解:如图,过点D分别作AE,AF的垂线,交AE于点M,交AF于点N,则∠CMD=∠BND=90°.∵ AD是∠EAF的平分线,∴ DM=DN.
∵ ∠ACD+∠ABD=180°,∠ACD+∠MCD=180°,∴ ∠MCD=∠NBD.在△CDM和△BDN中,∵ ∠CMD=∠BND=90°,∠MCD=∠NBD,DM=DN,∴ △CDM≌△BDN.∴ CD=BD
第6题答案
第6题答案
1
2
3
4
5
6
7
7. 如图,在△ABC中,∠BAC=60°,∠ABC=80°,∠BAC与∠ABC的平分线AD与BE交于点F.求证:AB+BD=AE+BE.
1
2
3
4
5
6
7
解:∵ ∠BAC=60°,∠ABC=80°,∴ ∠C=180°-(∠BAC+∠ABC)=180°-(60°+80°)=40°.∵ BE是∠ABC的平分线,
∴ ∠EBC=∠ABC=40°.∴ ∠C=∠EBC.∴ BE=EC.如图,过点D作DH∥BE,交AC于点H,则∠HDC=∠EBC=40°.∴ ∠HDC=∠C.
∴ HD=HC.∴ ∠AHD=∠HDC+∠C=40°+40°=80°.∴ ∠ABD=∠AHD.∵ AD是∠BAC的平分线,∴ ∠BAD=∠HAD.在△ABD和△AHD中,∵ ∴ △ABD≌△AHD.∴ AB=AH,BD=HD.∵ HD=HC,∴ BD=HC.∴ AB+BD=AH+HC=AC.又∵ BE=EC,∴ AE+BE=AE+EC=AC.∴ AB+BD=AE+BE
第7题答案
1
2
3
4
5
6
7
同课章节目录
